A=1/2+1/4+1/8+1/16/1/32+1/64
tính tổng
1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64
Tính nhanh
Đặt \(A=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+\dfrac{1}{2^4}+\dfrac{1}{2^5}+\dfrac{1}{2^6}\)
\(\Rightarrow2A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+\dfrac{1}{2^4}+\dfrac{1}{2^5}\)
\(\Rightarrow A=2A-A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^5}-\dfrac{1}{2}-\dfrac{1}{2^2}-...-\dfrac{1}{2^6}=1-\dfrac{1}{2^6}\)
Tính tổng A = 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64
Ta có : \(A=\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+...+\dfrac{1}{64}\)
\(A=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^6}\)
\(\Rightarrow2A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^5}\)
\(\Rightarrow2A-A=\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^5}\right)-\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^6}\right)\)
\(\Rightarrow A=1-\dfrac{1}{2^6}=1-\dfrac{1}{64}=\dfrac{63}{64}\)
\(A=\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+\dfrac{1}{32}+\dfrac{1}{64}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{8}+...+\dfrac{1}{32}-\dfrac{1}{64}\)
\(=1-\dfrac{1}{64}\)
\(=\dfrac{63}{64}\)
5 tính tổng sau bằng cách hợp lý.b,A= 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64
Lời giải:
$A=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}$
$2\times A=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}$
$2\times A-A=(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32})-(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64})$
$A=1-\frac{1}{64}=\frac{63}{64}$
A=1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64
2A = 2.(1/2+1/4+1/8+1/16+1/32+1/64)
= 1 + 1/2+1/4+1/8+1/16+1/32
=> 2A - A = (1+1/2+1/4+1/8+1/16+1/32) - (1/2+1/4+1/8+1/16+1/32+1/64)
=> A = 1 - 1/64
= 63/64
Nếu tổng này kéo dài mãi mãi thì kết quả là..........:tổng A=1/2+1/4+1/8+1/16+1/32+...........
\(A=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+.....\)
Đặt \(A=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^n}\)
\(2A=1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{n-1}}\)
\(2A-A=1-\frac{1}{2^n}\)
Tổng là \(A=1-\frac{1}{2^n}\)
B=2*4+2*4*8+4*8*16+8*16*32 / 3*4+2*6*8+4*12*16+8*24*32 các bạn có thể giả bằng 1 số nhân với 1 tổng ko ?
Tính S= 1+1/2+1/4+1/8+1/16+1/32
Tính tổng A=1.2+2.3+3.4+...+98.99
BÀI 1:
\(S=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\)
\(S=1+\frac{1}{1.2}+\frac{1}{2.2}+\frac{1}{2.4}+\frac{1}{4.4}+\frac{1}{4.8}\)
\(S=1+1-\frac{1}{2}+\frac{1}{2}-\frac{1}{2}+\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{4}+\frac{1}{4}-\frac{1}{8}\)
\(S=1+1-\frac{1}{8}\)
\(S=\frac{15}{8}\)
BÀI 2:
\(A=1.2+2.3+3.4+...+98.99\)
\(\Rightarrow3A=1.2.3+2.3.3+3.4.3+...+98.99.3\)
\(3A=1.2.\left(3-0\right)+2.3.\left(4-1\right)+3.4.\left(5-2\right)+...+98.99.\left(100-97\right)\)
\(3A=1.2.3+2.3.4-1.2.3+3.4.5-2.3.4+...+98.99.100-97.98.99\)
\(3A=\left(1.2.3+2.3.4+3.4.5+98.99.100\right)-\left(1.2.3+2.3.4+...+97.98.99\right)\)
\(3A=98.99.100\)
\(3A=970200\)
\(\Rightarrow A=970200:3\)
\(A=323400\)
CHÚC BN HỌC TỐT!!!
Tính tổng: S= 1/2+1/4+ 1/8+ 1/16+1/32+1/64+1/128
Cộng thêm 1/2 vào biểu thức đã cho, có:
S + 1/2= 1/2+1/4+ 1/8+ 1/16+1/32+1/64+1/128
Nhận xét:
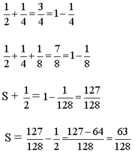
Tính tổng A= 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 . Ai giúp mình bài này với nhá. 😁😁
Ta có:2A=\(2+1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}\)
2A-A=\(\left(2+1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}\right)-\left(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\right)\)
\(=2-\frac{1}{32}=\frac{63}{32}=A\)
Ta có: \(A=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\)
\(\Rightarrow A=1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+\frac{1}{2^5}\)
\(\Rightarrow2A=2+1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}\)
\(\Rightarrow2A-A=\left(2+1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}\right)-\left(1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+\frac{1}{2^5}\right)\)
\(\Rightarrow A=1-\frac{1}{2^5}=\frac{31}{32}\)
Vậy \(A=\frac{31}{32}\)
1/2=1- 1/2
1/4=1/2 -1/4
A=1+1-1/2+1/2-1/4+1/8-1/8+1/8-1/16+1/16-1/32
A=1+1-1/36
71/36
Tính tổng
A)1/2+1/4+1/8+1/16
B)75/100+18/21+19/32+1/4+3/21+13/32