Cho đừong thẳng d và điểm A nằm ngoài (O) ; (O) và A nằm cùng phía đối với d. Xác định vị trí của K trên d sao cho góc tạo bởi tia KA với d bằng góc tạo bởi tia KB với d bằng nhau? Với B là tiếp điểm kẻ từ K của (O).
ND
Những câu hỏi liên quan
Cho đừong thẳng d và điểm A nằm ngoài (O) ; (O) và A nằm cùng phía đối với d. Xác định vị trí của K trên d sao cho góc tạo bởi tia KA với d bằng góc tạo bởi tia KB với d bằng nhau? Với B là tiếp điểm kẻ từ K của (O).
Từ một điểm M nằm ngoài đương tròn (O) với OM 2R, vẽ hai tiếp tuyến MA,MB đến đường tròn (A,B là hai tiếp điểm). Qua A vẽ đừong thẳng song song với MB,cắt đường tròn tại E,đoạn thẳng ME cắt đường tròn tại F. Hai ường thẳng AF và MB cắt nhau tại I.a) Chứng minh tứ giác MAOB nội tiếp đường tròn.b) Tam giác ABM là tam giác gì?Vì sao?c)Chứng Minh IB^2IF.IAd) Chứng minh M,F,O,E thẳng hàng
Đọc tiếp
Từ một điểm M nằm ngoài đương tròn (O) với OM = 2R, vẽ hai tiếp tuyến MA,MB đến đường tròn (A,B là hai tiếp điểm). Qua A vẽ đừong thẳng song song với MB,cắt đường tròn tại E,đoạn thẳng ME cắt đường tròn tại F. Hai ường thẳng AF và MB cắt nhau tại I.
a) Chứng minh tứ giác MAOB nội tiếp đường tròn.
b) Tam giác ABM là tam giác gì?Vì sao?
c)Chứng Minh IB^2=IF.IA
d) Chứng minh M,F,O,E thẳng hàng
Từ một điểm M ở bên ngoài đường tròn tâm O, vẽ hai tiếp tuyến MA, MB với đường tròn (O)( A, B là các tiếp điểm). Gọi E là trung điểm của đoạn thẳng MA, tia EB cắt đường tròn (O) tại C. Tia MC cắt đường tròn (O) tại điểm thứ hai là D. Chứng minh rằng:
a. Tứ giác MAOB nội tiếp;
b. EA2 = EC.EB;
c. BD // MA.
Từ một điểm M nằm ngoài đương tròn (O) với OM 2R, vẽ hai tiếp tuyến MA,MB đến đường tròn (A,B là hai tiếp điểm). Qua A vẽ đừong thẳng song song với MB,cắt đường tròn tại E,đoạn thẳng ME cắt đường tròn tại F. Hai ường thẳng AF và MB cắt nhau tại I.a) Chứng minh tứ giác MAOB nội tiếp đường tròn.b) Tam giác ABM là tam giác gì?Vì sao?c)Chứng Minh IB^2IF.IAd) Chứng minh M,F,O,E thẳng hàng
Đọc tiếp
Từ một điểm M nằm ngoài đương tròn (O) với OM = 2R, vẽ hai tiếp tuyến MA,MB đến đường tròn (A,B là hai tiếp điểm). Qua A vẽ đừong thẳng song song với MB,cắt đường tròn tại E,đoạn thẳng ME cắt đường tròn tại F. Hai ường thẳng AF và MB cắt nhau tại I.
a) Chứng minh tứ giác MAOB nội tiếp đường tròn.
b) Tam giác ABM là tam giác gì?Vì sao?
c)Chứng Minh IB^2=IF.IA
d) Chứng minh M,F,O,E thẳng hàng
Bạn tự vẽ hình nha
a)Xét tứ giác MAOB có:
\(\widehat{MAO}\)=90'(vì MA là tiếp tuyến của (O))
\(\widehat{MBO}\)=90'(vì MB là tiếp tuyến của (O))
Suy ra \(\widehat{MAO}\)+\(\widehat{MBO}\)=90'+90'=180'
Vậy tứ giác MAOB nội tiếp
b)Xét tam giác ABM có:
MA=MB(tính chất hai tiếp tuyến cắt nhau)
Do đó tam giác MAB là tam giác cân tại M
c)Xét tam giác IBF và IAB có:
\(\widehat{BIA}\)là góc chung
\(\widehat{IBF}\)=\(\widehat{IAB}\)(cùng bằng 1/2 sđ\(\widebat{BF}\))
Do đó tam giác IBF đồng dạng với IAB
Suy ra \(\frac{IB}{IF}=\frac{IA}{IB}\)
<=>\(IB^2=IA.IF\)
Đúng 0
Bình luận (0)
Cho đường thẳng d, điểm A nằm trên đường thẳng d, điểm B nằm ngoài đường thẳng d. Hãy dựng đường tròn (O) đi qua điểm B và tiếp xúc với đường thẳng d tại A.
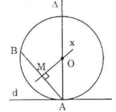
Đường tròn (O) tiếp xúc với d nên d là tiếp tuyến của (O) hay d vuông góc với bán kính của (O) tại tiếp điểm A. Suy ra tâm O của đường tròn nằm trên đường thẳng vuông góc với d tại A.
Lại có (O) qua B nên tâm O của đường tròn nằm trên đường trung trực của AB.
Vậy tâm O là giao điểm của đường vuông góc với d tại A và đường trung trực của AB.
Đúng 0
Bình luận (0)
Cho đường thẳng d, điểm A nằm trên đường thẳng d, điểm B nằm ngoài đường thẳng d. Hãy dựng đường tròn (O) đi qua điểm B và tiếp xúc với đường thẳng d tại A.
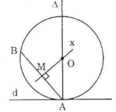
Đường tròn (O) tiếp xúc với d nên d là tiếp tuyến của (O) hay d vuông góc với bán kính của (O) tại tiếp điểm A. Suy ra tâm O của đường tròn nằm trên đường thẳng vuông góc với d tại A.
Lại có (O) qua B nên tâm O của đường tròn nằm trên đường trung trực của AB.
Vậy tâm O là giao điểm của đường vuông góc với d tại A và đường trung trực của AB.
Đúng 0
Bình luận (0)
Cho điểm A nằm trên đường thẳng d, điểm B nằm ngoài đường thẳng d. Dựng đường tròn (O) đi qua A và B nhận đường thẳng d làm tiếp tuyến.
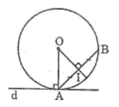
* Phân tích
- Giả sử dựng được đường tròn (O) qua A, B và tiếp xúc với d. Khi đó đường tròn (O) phải tiếp xúc với d tại A
- Đường tròn (O) đi qua A và B nên tâm O nằm trên đường trung trực của AB
- Đường tròn (O) tiếp xúc với d tại A nên điểm O nằm trên đường thẳng vuông góc với d tại điểm A
* Cách dựng
- Dựng đường thẳng trung trực của AB
- Dựng đường thẳng đi qua A và vuông góc với d. Đường thẳng này cắt đường trung trực của AB tại O
- Dựng đường tròn (O; OA) ta được đường tròn cần dựng
* Chứng minh
Vì O nằm trên đường trung trực của AB nên OA = OB. Khi đó đường tròn (O; OA) đi qua hai điểm A và B
Đúng 0
Bình luận (0)
Cho đường thẳng d, điểm A nằm trên đường d, điểm B nằm ngoài đường thẳng d. Hãy dựng đường tròn (O) đi qua điểm B và tiếp xúc với đường thẳng d tại A
Phân tích:
Giả sử đã dựng được đường tròn thỏa mãn đề bài.
Tâm O thỏa mãn hai điều kện:
- O nằm trên đường trung trực của AB (vì đường tròn đi qua A và B).
- O nằm trên đường thẳng vuông góc với d tại A (vì đường tròn tiếp xúc với đường thẳng d tại A).
Vậy O là giao điểm của hai đường thẳng nói trên.
Cách dựng:
- Dựng đường trung trực m của AB.
- Từ A dựng một đường thẳng vuông góc với d cắt đường thẳng m tại O.
- Dựng đường tròn (O;OA). Đó là đường tròn phải dựng.
Chứng minh:
Vì O nằm trên đường trung trực của AB nên OA=OB, do đó đường tròn (O;OA) đi qua A và B.
Đường thẳng d⊥OAd⊥OA tại A nên đường thẳng d tiếp xúc với đường tròn (O) tại A.
Biện luận: Bài toán luôn có nghiệm hình.
Đúng 0
Bình luận (0)
Cho điểm A nằm trên đường thẳng d, điểm B nằm ngoài đường thẳng d. Dựng đường tròn (O) đi qua A và B, nhận đường thẳng d làm tiếp tuyến ?
Cho 5 điểm A; B; C; D; O sao cho 3 điểm A; B; C cùng thuộc một đường thẳng d; 3 điểm B, C, D thẳng hàng và 3 điểm C, D, O không thẳng hàng. Hỏi điểm nào nằm ngoài đường thẳng d A. O, A B. O C. D D. C, D
Đọc tiếp
Cho 5 điểm A; B; C; D; O sao cho 3 điểm A; B; C cùng thuộc một đường thẳng d; 3 điểm B, C, D thẳng hàng và 3 điểm C, D, O không thẳng hàng. Hỏi điểm nào nằm ngoài đường thẳng d
A. O, A
B. O
C. D
D. C, D
Đáp án là B
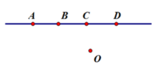
Vì ba điểm A; B; C thuộc d và B, C, D thẳng hàng nên D ∈ d
Mà C, D ∈ d nên C, D, O không thẳng hàng thì O ∉ d
Vậy điểm O không thuộc đường thẳng d.
Đúng 0
Bình luận (0)



