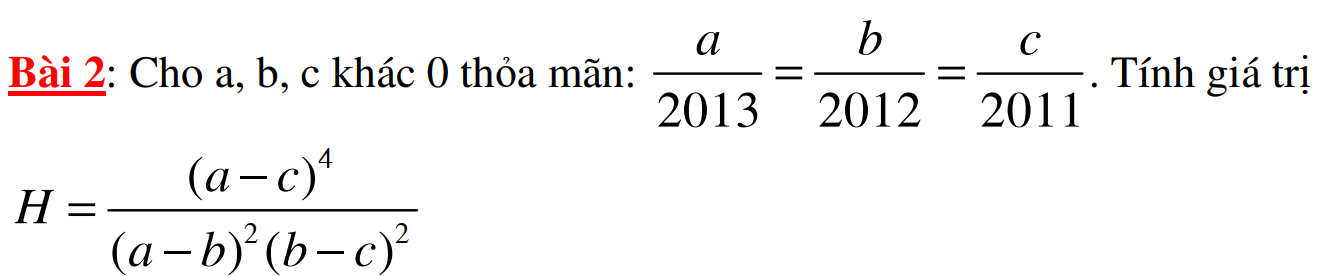
mình đag cần rất rất gấp. Mọi ng giúp mình vớiiiiiiiiiiii ak.
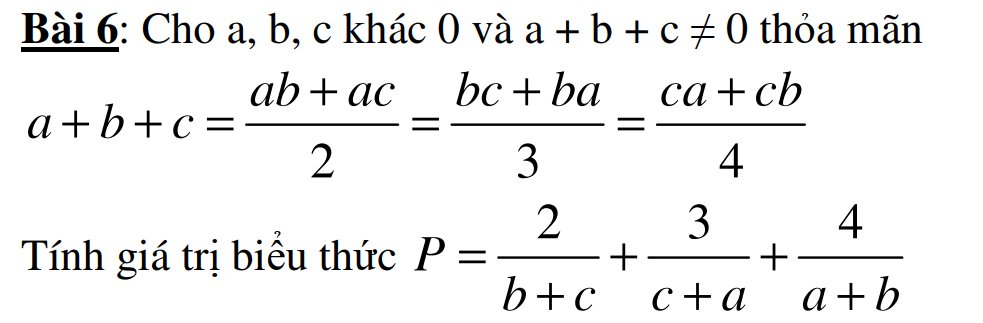
mình đag cần rất rất gấp. Mọi ng giúp mình vớiiiiiiiiiiii ak. mình sẽ tick
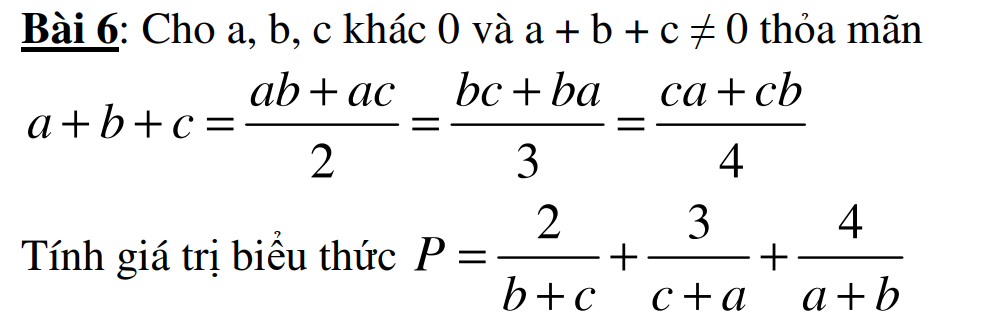
mình đag cần rất rất gấp. Mọi ng giúp mình vớiiiiiiiiiiii ak. mình sẽ tick
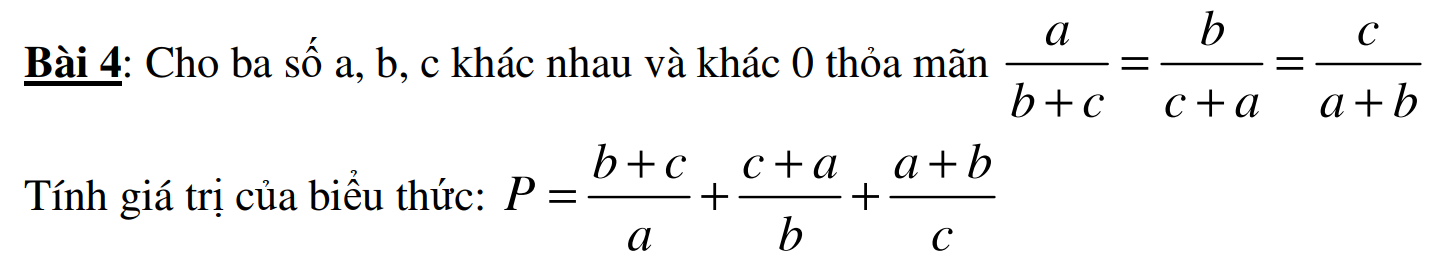
mình đag cần rất rất gấp. Mọi ng giúp mình vớiiiiiiiiiiii ak. mình sẽ tick
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{b+c}=\dfrac{b}{c+a}=\dfrac{c}{a+b}=\dfrac{a+b+c}{2\left(a+b+c\right)}=\dfrac{1}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}b+c=2a\\c+a=2b\\a+b=2c\end{matrix}\right.\)
\(\Rightarrow P=\dfrac{b+c}{a}+\dfrac{c+a}{b}+\dfrac{a+b}{c}=\dfrac{2a}{a}+\dfrac{2b}{b}+\dfrac{2c}{c}=2+2+2=6\)
P=
\(\dfrac{b+c}{a}+\dfrac{c+a}{b}+\dfrac{a+b}{c}=\dfrac{a}{b+c}.\left(\dfrac{b+c}{a}+\dfrac{c+a}{b}+\dfrac{a+b}{c}\right):\left(\dfrac{a}{b+c}\right)=\left(\dfrac{b+c}{a}.\dfrac{a}{b+c}+\dfrac{c+a}{b}.\dfrac{a}{b+c}+\dfrac{a+b}{c}.\dfrac{a}{b+c}\right):\dfrac{a}{b+c}=\left(\dfrac{b+c}{a}.\dfrac{a}{b+c}+\dfrac{c+a}{b}.\dfrac{b}{c+a}+\dfrac{a+b}{c}.\dfrac{c}{a+b}\right):\dfrac{a}{b+c}=\left(1+1+1\right):\dfrac{a}{b+c}=3.\dfrac{b+c}{a}=\dfrac{3b+3c}{a}\)
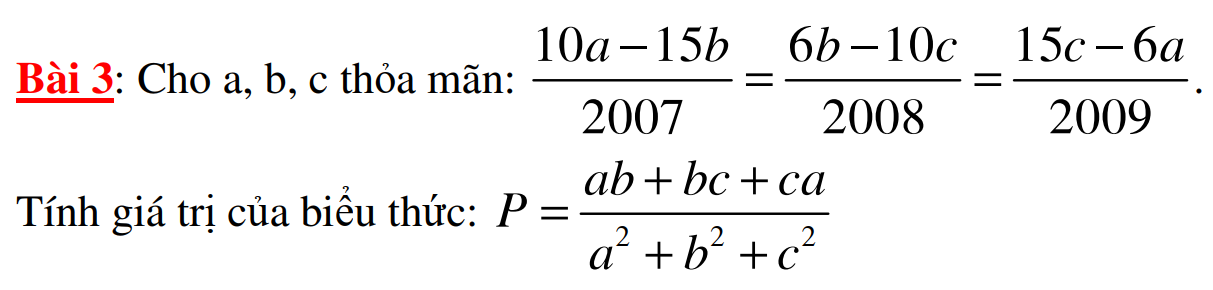
mình đag cần rất rất gấp. Mọi ng giúp mình vớiiiiiiiiiiii ak. mình sẽ tick
Lời giải:
Bổ sung điều kiện $a,b,c$ không thể đồng thời bằng $0$
Từ đkđb suy ra:
\(\frac{6(10a-15b)}{2007.6}=\frac{15(6b-10c)}{15.2008}=\frac{10(15c-6a)}{10.2009}\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{6(10a-15b)}{2007.6}=\frac{15(6b-10c)}{15.2008}=\frac{10(15c-6a)}{10.2009}=\frac{6(10a-15b)+15(6b-10c)+10(15c-6a)}{2007.6+15.2008+10.2009}=0\)
\(\Rightarrow 10a-15b=6b-10c=15c-6a=0\)
\(\Leftrightarrow 10a=15b; 6b=10c; 15c=6a\Leftrightarrow \frac{a}{15}=\frac{b}{10}=\frac{c}{6}\)
Đặt $\frac{a}{15}=\frac{b}{10}=\frac{c}{6}=k$ thì: $a=15k, b=10k, c=6k$
Vì $a,b,c$ không thể đồng thời bằng $0$ nên $k\neq 0$
Khi đó:
$P=\frac{15k.10k+10k.6k+15k.6k}{(15k)^2+(10k)^2+(6k)^2}$
$=\frac{300k^2}{361k^2}=\frac{300}{361}$
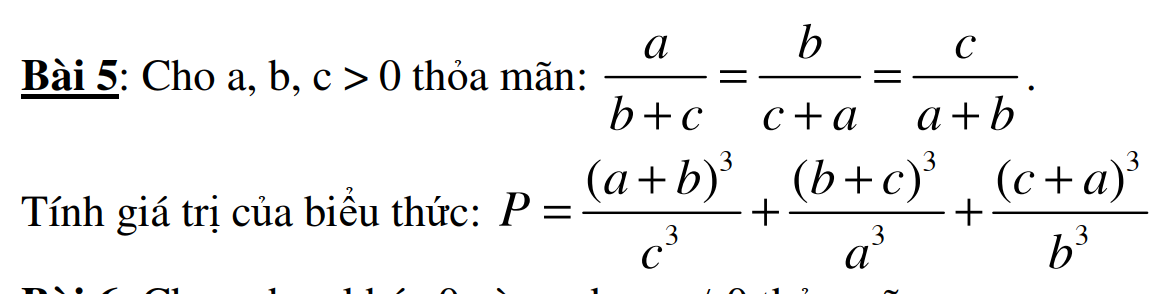
mình đag cần rất rất gấp. Mọi ng giúp mình vớiiiiiiiiiiii ak. mình sẽ tick
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{a}{b+c}=\dfrac{b}{c+a}=\dfrac{c}{a+b}=\dfrac{a+b+c}{2\left(a+b+c\right)}=\dfrac{1}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}2a=b+c\\2b=a+c\\2c=a+b\end{matrix}\right.\)
\(\Rightarrow P=\dfrac{\left(a+b\right)^3}{c^3}+\dfrac{\left(b+c\right)^3}{a^3}+\dfrac{\left(c+a\right)^3}{b^3}=\left(\dfrac{a+b}{c}\right)^3+\left(\dfrac{b+c}{a}\right)^3+\left(\dfrac{c+a}{b}\right)^3=\left(\dfrac{2c}{c}\right)^3+\left(\dfrac{2a}{a}\right)^3+\left(\dfrac{2b}{b}\right)^3=2^3+2^3+2^3=24\)
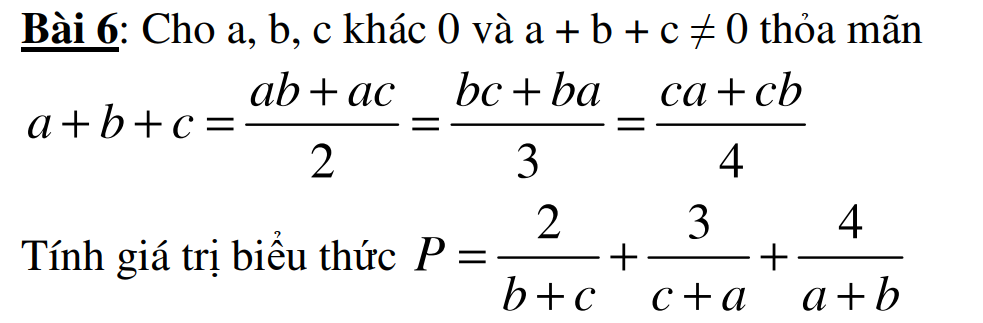
mình đag cần rất rất gấp. Mọi ng giúp mình vớiiiiiiiiiiii ak. mình sẽ tick
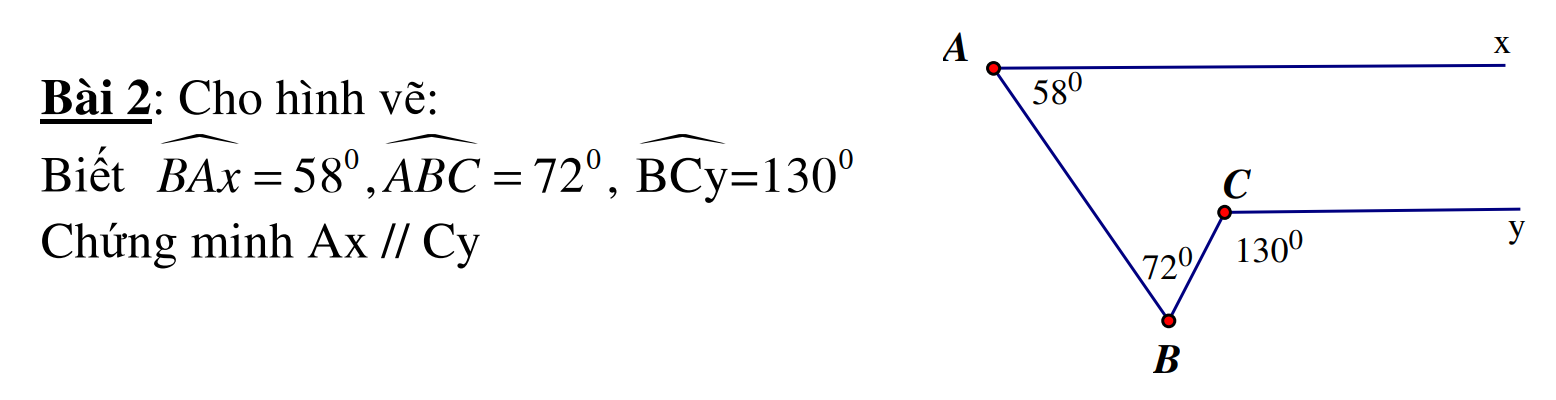
Mình đag cần rất rất gấp. mọi ng giúp mình vớiiiiiiiiiiii
từ điểm B kẻ \(Bz//Cy=>\angle\left(BCy\right)+\angle\left(CBz\right)=180^o\)(góc trong cùng phía)
\(=>\angle\left(CBz\right)=180^o-130^o=50^o\)
\(=>\angle\left(ABz\right)=\angle\left(ABC\right)+\angle\left(CBz\right)=50^o+72^o=122^o\)
\(=>\angle\left(BAx\right)+\angle\left(ABz\right)=180^o\)
mà 2 góc này ở vị trí trong cùng phía
\(=>Ax//Bz=>Ax//Cy\)
\(A=\left|x+2\right|+\left|x-3\right|\)
Tìm GTNN
Mình đag cần rất rất gấp . mọi ng giúp mình vớiiiiiiiiiiii
A = I x + 2 I + I x - 3 I
GTNN là 1 nha bạn
\(A=\left|x+2\right|+\left|x-3\right|=\left|x+2\right|+\left|3-x\right|\ge\left|x+2+3-x\right|=5\)
Dấu ''='' xảy ra khi \(\left(x+2\right)\left(3-x\right)\ge0\Leftrightarrow-2\le x\le3\)
Vậy GTNN của A bằng 5 tại \(-2\le x\le3\)
\(A=|x+2|+|x-3|\)
Sử dụng công thức \(|x|\ge x\). Dấu "=" xảy ra \(\Leftrightarrow x=0\)
\(|x|=|-x|\)
\(A=|x+2|+|3-x|\)
Ta có: \(|x+2|\ge x+2;|3-x|\ge3-x\)
\(\Rightarrow A\ge x+2+3-x\)
\(\Rightarrow A\ge5\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}x+2\ge0\\3-x\ge0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x\ge-2\\x\le3\end{cases}}\)
Vậy GTNN của A = 5 khi -2 < x < 3

Mình đag cần rất rất gấp. mọi ng giúp mình với ak
ta có \(\left(x-4\right)\left(6-x\right)\le\left(\frac{x-4+6-x}{2}\right)^2=1\) (bất đẳng thức cauchy)
mà \(\left|y+1\right|\ge0\Rightarrow\left|y+1\right|+2\ge2>1\)
Vậy phương trình trên vô nghiệm
Llllllllll