\(9\text{x}-7i>3\left(3\text{x}-7u\right)\)
bai toan tinh yeu
A=\(\frac{5x\left(2^2\text{x}3^2\right)^9\text{x}\left(2^2\right)^6-2\text{x}\left(2^2\text{x}3\right)^{14}\text{x}3^4}{\text{ }5\text{x}2^{28}\text{x}3^{18}-7\text{x}2^{29}\text{x}3^{18}}\)
\(\frac{5.2^{18}.3^{18}.2^{12}-2.2^{28}.3^{14}.3^4}{5.2^{28}.3^{18}-7.2^{29}.3^{18}}=\frac{5.2^{30}.3^{18}-2^{29}.3^{18}}{5.2^{28}.3^{18}-7.2^{29}.3^{18}}=\frac{2^{29}.3^{18}\left(5.2-1\right)}{2^{28}.3^{18}\left(5-7.2\right)}\)
\(\frac{2^{29}.3^{18}.9}{2^{28}.3^{18}.-9}=\frac{2.9}{-9}=-2\)
ko phải tìm x nha
Tìm x:
\(x-\text{[}\left(\frac{3x+3}{4}\right):2\text{]}=\text{[}\left(\frac{9+x}{6}\right):2\text{]} \)
Mọi người giúp em với :((
A= \(\left(\frac{x-\text{3√x}}{x-9}-1\right)\)\(\left(\frac{9-x}{x+\text{√}x-6}+\frac{\text{√}x-3}{\text{√}x-2}-\frac{\text{√}x+2}{\text{√}x+3}\right)\)với x<0 ; x≠2 ; x≠9
a) rút gọn biểu thức A
cảm ơn mọi người <3
\(A=\left(\frac{x-3\sqrt{x}}{x-9}-1\right)\left(\frac{9-x}{x+\sqrt{x}-6}+\frac{\sqrt{x}-3}{\sqrt{x}-2}-\frac{\sqrt{x}+2}{\sqrt{x}+3}\right)\)
\(=\left(\frac{\sqrt{x}}{\sqrt{x}+3}-1\right)\left(\frac{9-x+x-9-x+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\right)\)
\(=\frac{-3}{\sqrt{x}+3}.\frac{2-\sqrt{x}}{\sqrt{x}+3}\)
\(=\frac{3\sqrt{x}-6}{\left(\sqrt{x}+3\right)^2}\)
a, \(\text{[}\left(x-y\right)^3+3\left(x-y\right)\text{]}:\dfrac{1}{3}\left(x-y\right)\)
b, \(\left(8x^3-27y^3\right):\left(2x-3y\right)\)
c, \(\text{[}5\left(x+2y\right)^6-6\left(x+2y\right)^5\text{]}:2\left(x+2y\right)^4\)
a: \(=\left(x-y\right)^3:\dfrac{1}{3}\left(x-y\right)+3\left(x-y\right):\dfrac{1}{3}\left(x-y\right)\)
=3(x-y)^2+9
b: \(=\dfrac{\left(2x-3y\right)\left(4x^2+6xy+9y^2\right)}{2x-3y}=4x^2+6xy+9y^2\)
c: \(=\dfrac{5\left(x+2y\right)^6}{2\left(x+2y\right)^4}-\dfrac{6\left(x+2y\right)^5}{2\left(x+2y\right)^4}=\dfrac{5}{2}\left(x+2y\right)^2-3\left(x+2y\right)\)
tìm x, biết:
a) \(\left(3\text{x}+2\right)\left(x-1\right)-3\left(x+1\right)\left(x-2\right)=4\)
b) \(\left(3\text{x}-5\right)\left(7-5\text{x}\right)-\left(5\text{x}+2\right)\left(2-3\text{x}\right)=4\)
Với những giá trị nào của m thì các hàm số sau đây là hàm số bậc nhất?
a. y = (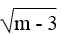
b. S = 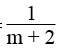
Không chép mạng nha, giúp vs, gấp lắm rồi!
Hàm số y=m−3.x+23 là hàm số bậc nhất khi hệ số của x là a=m−3≠0
Ta có: m−3≠0⇔m−3>0⇔m>3
Vậy khi m>3 thì hàm số y=m−3x+23 là hàm số bậc nhất
Câu b
S=1m+2t−34 (t là biến số).
Phương pháp giải:
Để hàm số được cho bởi công thức y=ax+b là hàm số bậc nhất thì a≠0 .
Lời giải chi tiết:
Hàm số S=1m+2t−34 là hàm số bậc nhất khi hệ số của t là a=1m+2≠0
Ta có: 1m+2≠0⇔m+2≠0⇔m≠−2
Vậy khi m≠−2 thì hàm số S=1m+2t−34 là hàm số bậc nhất.
Lời giải và đáp án
Đây là dạng toán hàm số bậc nhất nha bạn, áp dụng vào và làm là được!
\(a.\)\(\text{Hàm số }y=(\sqrt{m-3)}x+\frac{2}{3}\) \(\text{là hàm số bậc nhất khi hệ số của }\)\(x\)\(\text{là}\)\(a=\sqrt{m-3\ne}0\)
\(\text{Ta có: }\sqrt{m-3}m-3\ne0\Leftrightarrow m-3>0\Leftrightarrow m>3\)
\(\text{Vậy khi}\) \(m>3\)\(\text{thì hàm số }y=(\sqrt{m-3})x+\frac{2}{3}\text{ là hàm số bậc nhất.}\)
\(b.\) \(\text{Hàm số }S=:\frac{1}{m+2}t-\frac{3}{4}\text{là hàm số bậc nhất khi hệ số của }t\text{ là }a=:\frac{1}{m+2}\ne0\)
\(\text{Ta có: }\frac{1}{m+2}\ne0\Leftrightarrow m+2\ne0\Leftrightarrow m\ne-2\)
\(\text{Vậy khi}\) \(m\ne-2\text{thì hàm số}\)\(S=:\frac{1}{m+2}t-\frac{3}{4}\text{là hàm số bậc nhất.}\)
Tính:
1. \(\frac{x^2}{x^2-x}-\frac{x^2}{x+1}-\frac{2\text{x}}{x^2-1}\)
2. \(\frac{4x^2-3x+5}{x^3-1}-\frac{1-2\text{x}}{x^2+x+1}-\frac{6}{x-1}\)
3. \(\frac{5}{2\text{x}^2+6\text{x}}-\frac{4-3\text{x}^2}{x^2-9}-3\)
4. \(\frac{7}{8x^2-18}+\frac{1}{2\text{x}^2+3\text{x}}-\frac{1}{4\text{x}-6}\)
5. \(\frac{1}{x\left(x+1\right)}+\frac{1}{\left(x+1\right)\left(x+2\right)}+...+\frac{1}{\left(x+9\right)\left(x+10\right)}\)
Các bạn giúp mình bài toán sau
\(\left(x+2\right)^3\text{-}\left(x+1\right)\left(x^2\text{-}x+1\right)=10\)
\(\left(x\text{-}1\right)^3\text{-}\left(x\text{-}2\right)\left(x^2+x+4\right).3x\left(x+1\right)=0\)
\(\left(x\text{-}3\right)^2\text{-}\left(x\text{-}2\right)\left(x^2+2x+4\right)\text{-}9x\left(x\text{-}1\right)=0\)
đề bài là tìm x à bạn? đề có cho điều kiện ko vậy ạ? (ví dụ như x nguyên?)
\(\left(x-1\right)^3+\left(x^3-8\right).3x.\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right).\left[\left(x-1\right)^2+\left(x^3-8\right).3x\right]=0\)
TH1: \(x-1=0\Leftrightarrow x=1\)
TH2: \(\left(x-1\right)^2+\left(x^3-8\right).3x=0\)
\(\Rightarrow\left[{}\begin{matrix}\left(x-1\right)^2=0\\\left(x^3-8\right).3x=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left\{{}\begin{matrix}x^3-8=0\\3x=0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\\left\{{}\begin{matrix}x=2\\x=0\end{matrix}\right.\end{matrix}\right.\)
Vậy \(x\in\left\{0;1;2\right\}\)
Tìm x, biết:
a) \(x\left(x-1\right)-x^2+2\text{x}=5\)
b) \(8\left(x-2\right)-2\left(3\text{x}-4\right)=2\)
c) \(\left(3\text{x}+2\right)\left(x-1\right)-3\left(x+1\right)\left(x-2\right)=4\)
d) \(\left(3\text{x}-5\right)\left(7-5\text{x}\right)-\left(5\text{x}+2\right)\left(2-3\text{x}\right)=4\)