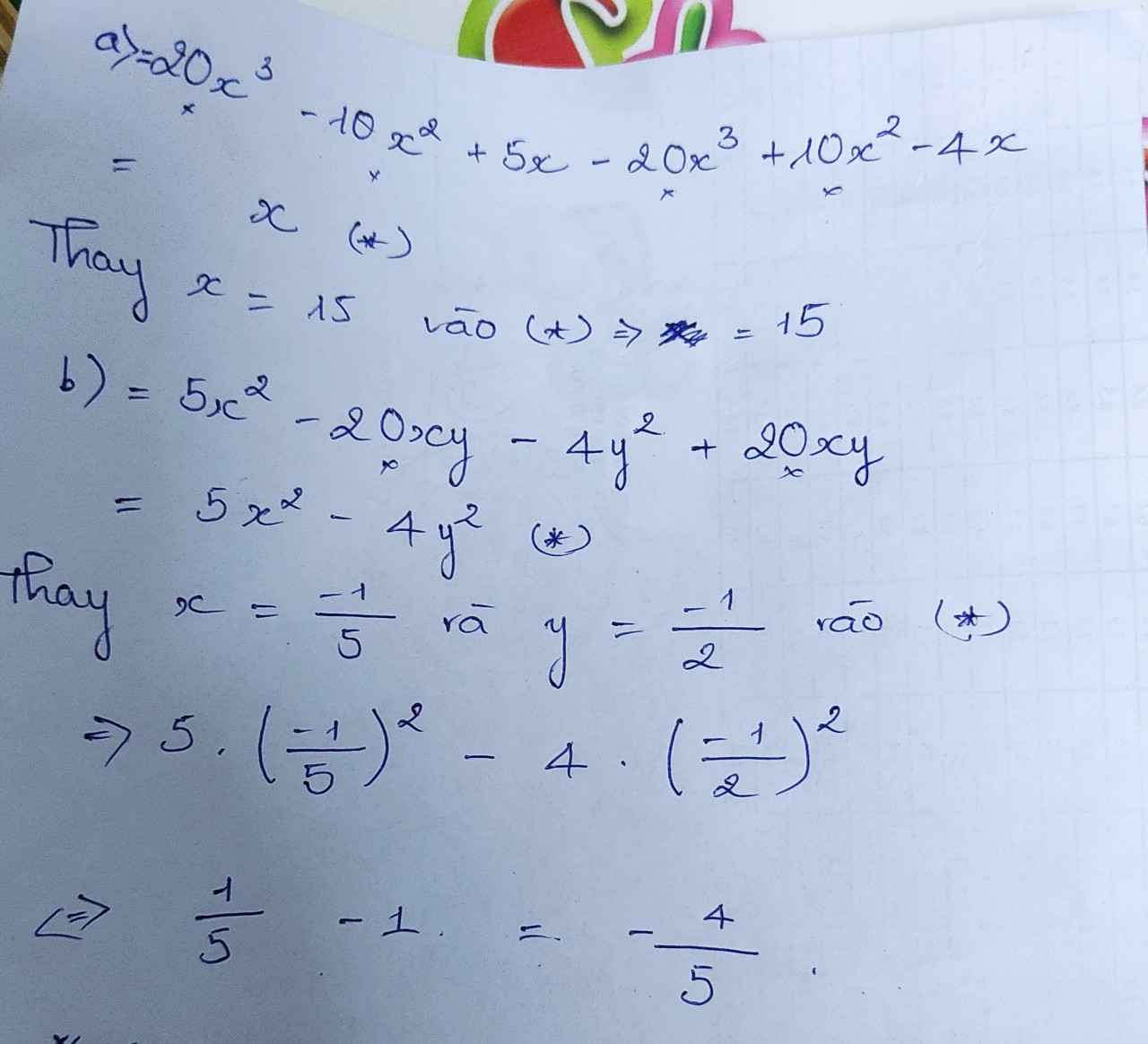B=\(\left(5x-11\right)^2-\left(10x-22\right)\left(5x-9\right)+\left(5x-9\right)^2\)
KP
Những câu hỏi liên quan
BT3: Tìm x
\(a,\left(x+2\right)^2-9=0\)
\(b,x^2-2x+1=25\)
\(c,\left(5x+1\right)^2-\left(5x-3\right)\left(5x+3\right)=30\)
\(d,\left(x-1\right)\left(x^2+x+1\right)+x\left(x+2\right)\left(2-x\right)=5\)
\(a,\left(x+2\right)^2-9=0\\ \Leftrightarrow\left(x+2-3\right)\left(x+2+3\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-5\end{matrix}\right.\\ Vậy\dfrac{ }{ }S=\left\{1;-5\right\}\)
\(b,x^2-2x+1=25\\ \Leftrightarrow\left(x-1\right)^2=25\\ \Leftrightarrow\left(x-1\right)^2-25=0\\ \Leftrightarrow\left(x-1-5\right)\left(x-1+5\right)=0\\ \Leftrightarrow\left(x-6\right)\left(x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=6\\x=-4\end{matrix}\right.\\ Vậy\dfrac{ }{ }S=\left\{6;-4\right\}\)
\(c,\left(5x+1\right)^2-\left(5x-3\right)\left(5x+3\right)=30\\ \Leftrightarrow25x^2+10x+1-25x^2+9=30\\ \Leftrightarrow25x^2+10x-25x^2=30-1-9\\ \Leftrightarrow10x=20\\ \Leftrightarrow x=2\\ Vậy\dfrac{ }{ }S=\left\{2\right\}\)
\(d,\left(x-1\right)\left(x^2+x+1\right)+x\left(x+2\right)\left(2-x\right)=5\\ \Leftrightarrow x^3-1-x\left(x^2-4\right)=5\\ \Leftrightarrow x^3-1-x^3+4x=5\\ \Leftrightarrow x^3-x^3+4x=5+1\\ \Leftrightarrow4x=6\\ \Leftrightarrow x=\dfrac{3}{2}\\ Vậy\dfrac{ }{ }S=\left\{\dfrac{3}{2}\right\}\)
Đúng 3
Bình luận (0)
a: =>(x+2-3)(x+2+3)=0
=>(x-1)(x+5)=0
=>x=1 hoặc x=-5
b: =>(x-1)^2=25
=>x-1=5 hoặc x-1=-5
=>x=-4 hoặc x=6
c: =>25x^2+10x+1-25x^2+9=30
=>10x+10=30
=>x+1=3
=>x=2
d: =>x^3-1-x(x^2-4)=5
=>x^3-1-x^3+4x=5
=>4x=6
=>x=3/2
Đúng 3
Bình luận (0)
\(8x^2-5x-22=\left(ax+11\right)\left(bx-2\right)\)
\(\Leftrightarrow\left(8x+11\right)\left(x-2\right)=\left(ax+11\right)\left(bx-2\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=8\\b=1\end{matrix}\right.\Rightarrow a-b=8-1=7\)
Bài 1. tính giá trị biểu thức.a. 5xleft(4x^2-2x+1right)-2xleft(10x^2-5x+2right) với x 15b.5xleft(x-4yright)-4yleft(y-5xright) tại xdfrac{-1}{5} và ydfrac{-1}{2}c.6xyleft(xy-y^2right)-8x^2left(x-y^2right)+5y^2left(x^2-xyright)với xdfrac{1}{2};y2giúp mik với mik đang cần gấp cảm ơn
Đọc tiếp
Bài 1. tính giá trị biểu thức.
a. \(5x\left(4x^2-2x+1\right)-2x\left(10x^2-5x+2\right)\) với x = 15
b.\(5x\left(x-4y\right)-4y\left(y-5x\right)\) tại \(x=\dfrac{-1}{5}\) và \(y=\dfrac{-1}{2}\)
c.\(6xy\left(xy-y^2\right)-8x^2\left(x-y^2\right)+5y^2\left(x^2-xy\right)\)với \(x=\dfrac{1}{2};y=2\)
giúp mik với mik đang cần gấp cảm ơn
\(\left(x-2\right)\left(x^2+6x-11\right)^2=\left(5x^2-10x=1\right)^2\)
Tìm x:8) 1-left(x-6right)4left(2-2xright)9)left(3x-2right)left(x+5right)010)left(x+3right)left(x^2+2right)011)left(5x-1right)left(x^2-9right)012)xleft(x-3right)+3left(x-3right)013)xleft(x-5right)-4x+20014)x^2+4x-50
Đọc tiếp
Tìm \(x\):
\(8\)) \(1-\left(x-6\right)=4\left(2-2x\right)\)
\(9\))\(\left(3x-2\right)\left(x+5\right)=0\)
\(10\))\(\left(x+3\right)\left(x^2+2\right)=0\)
\(11\))\(\left(5x-1\right)\left(x^2-9\right)=0\)
\(12\))\(x\left(x-3\right)+3\left(x-3\right)=0\)
\(13\))\(x\left(x-5\right)-4x+20=0\)
\(14\))\(x^2+4x-5=0\)
\(8,1-\left(x-6\right)=4\left(2-2x\right)\)
\(\Leftrightarrow1-x+6=8-8x\)
\(\Leftrightarrow-x+8x=8-1-6\)
\(\Leftrightarrow7x=1\)
\(\Leftrightarrow x=\dfrac{1}{7}\)
\(9,\left(3x-2\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-2=0\\x+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-5\end{matrix}\right.\)
\(10,\left(x+3\right)\left(x^2+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x^2+2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=\varnothing\end{matrix}\right.\)
Đúng 2
Bình luận (0)
`8)1-(x-5)=4(2-2x)`
`<=>1-x+5=8-6x`
`<=>5x=2<=>x=2/5`
`9)(3x-2)(x+5)=0`
`<=>[(x=2/3),(x=-5):}`
`10)(x+3)(x^2+2)=0`
Mà `x^2+2 > 0 AA x`
`=>x+3=0`
`<=>x=-3`
`11)(5x-1)(x^2-9)=0`
`<=>(5x-1)(x-3)(x+3)=0`
`<=>[(x=1/5),(x=3),(x=-3):}`
`12)x(x-3)+3(x-3)=0`
`<=>(x-3)(x+3)=0`
`<=>[(x=3),(x=-3):}`
`13)x(x-5)-4x+20=0`
`<=>x(x-5)-4(x-5)=0`
`<=>(x-5)(x-4)=0`
`<=>[(x=5),(x=4):}`
`14)x^2+4x-5=0`
`<=>x^2+5x-x-5=0`
`<=>(x+5)(x-1)=0`
`<=>[(x=-5),(x=1):}`
Đúng 1
Bình luận (0)
\(11,=>\left[{}\begin{matrix}5x-1=0\\x^2-9=0\end{matrix}\right.=>\left[{}\begin{matrix}x=\dfrac{1}{5}\\x=3\\x=-3\end{matrix}\right.\\ 12,=>\left(x+3\right)\left(x-3\right)=0\\ =>\left[{}\begin{matrix}x+3=0\\x-3=0\end{matrix}\right.=>\left[{}\begin{matrix}x=-3\\x=3\end{matrix}\right.\\ 13,=>x\left(x-5\right)-4\left(x-5\right)=0\\ =>\left(x-4\right)\left(x-5\right)=0\\ =>\left[{}\begin{matrix}x-4=0\\x-5=0\end{matrix}\right.=>\left[{}\begin{matrix}x=4\\x=5\end{matrix}\right.\)
\(14,=>x^2+5x-x-5=0\\ =>x\left(x+5\right)-\left(x+5\right)=0\\ =>\left(x-1\right)\left(x+5\right)=0\\ =>\left[{}\begin{matrix}x-1=0\\x+5=0\end{matrix}\right.=>\left[{}\begin{matrix}x=1\\x=-5\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Chứng minh đẳng thức sau \(\left(5x-11\right)^2+\left(4-5x\:\right)^2+2\left(5x\:-11\right)\left(4-5x\:\right)=49\)
Ta có (5x-11)2+(4-5x)2+2(5x-11)(4-5x)
=25x2-110x+121+16-40x+25x2+40x-50x2- 88+110x
=16-88+121
=49(đpcm)
TK MK NHA BN
Đúng 0
Bình luận (0)
\(\frac{3x}{5x+5y}-\frac{x}{10x-10y}\\ \left(\frac{3x}{1-3n}+\frac{2n}{3x+1}\right):\left(\frac{6x^2+10x}{1-6x+9x^2}\right)\\ \left(\frac{9}{x^3-9n}+\frac{1}{x+3}\right):\left(\frac{x}{3n+9}\right)\)
\(\frac{3x}{5x+5y}-\frac{x}{10x-10y}\)
= \(\frac{3x\left(x-y\right)}{5.2.\left(x+y\right)\left(x-y\right)}-\frac{x\left(x+y\right)}{10\left(x^2-y^2\right)}\)
= \(\frac{3x^2-3xy-x^2-xy}{10\left(x^2-y^2\right)}\)
= \(\frac{3x\left(x-y\right)}{10\left(x^2-y^2\right)}\)
= \(\frac{3x}{10\left(x+y\right)}\)
Đúng 0
Bình luận (0)
BÀI 1: GIẢI CÁC PHƯƠNG TRÌNH SAUa) left(2x-1right)^249b) left(5x-3right)^2-left(4x-7right)^20c) left(2x+7right)^2-9left(x+3right)^2d) left(x+2right)^29left(x^2-4x+4right)e) 4left(2x+7right)^2-9left(x+3right)^20f) left(5x^2-2x+10right)^2left(3x^2+10x-8right)^2
Đọc tiếp
BÀI 1: GIẢI CÁC PHƯƠNG TRÌNH SAU
a) \(\left(2x-1\right)^2=49\)
b) \(\left(5x-3\right)^2-\left(4x-7\right)^2=0\)
c) \(\left(2x+7\right)^2-9\left(x+3\right)^2\)
d) \(\left(x+2\right)^2=9\left(x^2-4x+4\right)\)
e) \(4\left(2x+7\right)^2-9\left(x+3\right)^2=0\)
f) \(\left(5x^2-2x+10\right)^2=\left(3x^2+10x-8\right)^2\)
a) 4 b) 0,6 hoặc 1,75 e) -3,5 hoặc -3
\(\left\{{}\begin{matrix}2x-5y=3\\6x-15y=10\end{matrix}\right.\)
\(\left\{{}\begin{matrix}5x+7y=11\\10x+14y=22\end{matrix}\right.\)
\(\left\{{}\begin{matrix}2x-5y=3\\6x-15y=10\end{matrix}\right.\)
Vì \(\dfrac{2}{6}=\dfrac{-5}{-15}\ne\dfrac{3}{10}\)
nên hệ phương trình vô nghiệm
\(\left\{{}\begin{matrix}5x+7y=11\\10x+14y=22\end{matrix}\right.\)
Vì \(\dfrac{5}{10}=\dfrac{7}{14}=\dfrac{11}{22}=\dfrac{1}{2}\)
nên hệ phương trình có vô số nghiệm
Đúng 0
Bình luận (0)