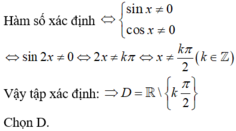tìm tập xác định y = sin^2x - 3sinx / (tanx -1 ) (cotx + 1) giúp mình với ạ
AN
Những câu hỏi liên quan
Giúp mình với ạ. Mọi người biết câu nào thì giải chi tiết giúp mình với (vì vào học chậm hơn các bạn nên ko hiểu gì hết ạ). Cảm ơn mn nhiều lắm.Tìm tập xác định của hàm sốa) yfrac{3sinx+5}{1+tan^2X}b) y frac{2-cotx}{1+cos2x}c) y frac{1}{cotx-sqrt{3}}d) y frac{sinx}{1-2sin^2x}
Đọc tiếp
Giúp mình với ạ. Mọi người biết câu nào thì giải chi tiết giúp mình với (vì vào học chậm hơn các bạn nên ko hiểu gì hết ạ). Cảm ơn mn nhiều lắm.
Tìm tập xác định của hàm số
a) y=\(\frac{3sinx+5}{1+tan^2X}\)
b) y= \(\frac{2-cotx}{1+cos2x}\)
c) y= \(\frac{1}{cotx-\sqrt{3}}\)
d) y= \(\frac{sinx}{1-2sin^2x}\)
a) ĐK: \(\cos x\ne0\)( vì tan x = sinx/cosx nên cos x khác 0)
<=> \(x\ne\frac{\pi}{2}+k\pi\); k thuộc Z
TXĐ: \(ℝ\backslash\left\{\frac{\pi}{2}+k\pi\right\}\); k thuộc Z
b) ĐK: \(1+\cos2x\ne0\Leftrightarrow\cos2x\ne-1\Leftrightarrow2x\ne\pi+k2\pi\Leftrightarrow x\ne\frac{\pi}{2}+k\pi\); k thuộc Z
=> TXĐ: \(ℝ\backslash\left\{\frac{\pi}{2}+k\pi\right\}\); k thuộc Z
c) ĐK: \(\hept{\begin{cases}\cot x-\sqrt{3}\ne0\\\sin x\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ne\frac{\pi}{6}+k\pi\text{}\text{}\\x\ne l\pi\end{cases}}\); k,l thuộc Z
=>TXĐ: ....
d) ĐK: \(1-2\sin^2x\ne0\Leftrightarrow\cos2x\ne0\Leftrightarrow2x\ne\frac{\pi}{2}+k\pi\Leftrightarrow x\ne\frac{\pi}{4}+\frac{k\pi}{2}\)
=> TXĐ:...
Xét bốn mệnh đề sau:
1
: Hàm số
y
s
inx
có tập xác định là
R
2
: Hàm số
y
c
osx
có tập xác định là
R
3
Hàm số
y
tan
x
có tập xác định là
R
4
Hàm số
y
cot...
Đọc tiếp
Xét bốn mệnh đề sau:
1 : Hàm số y = s inx có tập xác định là R
2 : Hàm số y = c osx có tập xác định là R
3 Hàm số y = tan x có tập xác định là R
4 Hàm số y = cot x có tập xác định là R
Tìm số phát biểu đúng.
A. 3
B. 2
C. 4
D. 1
Đáp án là B
• Hàm số y = sin x ; y = cos x có tập xác định D = ℝ .
• Hàm số y = tan x & y = cot x có tập xác định lần lượt D = ℝ \ π 2 + k π ; D = ℝ \ k π .
Đúng 0
Bình luận (0)
Tìm tập xác định cúa các hàm số sau:
a,y=\(\dfrac{cot2x}{sinx-cos3x}\)
b,y=\(\dfrac{1+tanx}{cosx+cos5x}\)
Mọi người giúp mình vs ạ!!!
A=√sin2x(1+cotx)+cos2x(1+tanx)
B=sin^2x-tan^2x/cos^2x-cot^2x CẦN GẤP Ạ1. Không biết yêu cầu đề bài là gì???
2. Biểu thức đề bài ko rõ ràng (ko biết căn thức tới đâu, đâu là tử số đâu là mẫu số).
Bạn cần ghi rõ yêu cầu đề bài, và sử dụng công cụ gõ công thức (kí hiệu khoanh đỏ trên khung soạn thảo) để mọi người đỡ mệt.

Đúng 0
Bình luận (0)
\(\sqrt{sin^2x\left(1+cotx\right)+cos^2x\left(1+tanx\right)}\)
Rút gọn giúp tui nha~~
Tập xác định của hàm số y = tan x + c o t x là
A. R
![]()
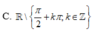
![]()
chứng minh: (sin^2x/1+cotx)-(cos^2x/1+tanx)=tanx-1
\(\dfrac{sin^2x}{1+cotx}-\dfrac{cos^2x}{1+tanx}=\dfrac{sin^2x}{1+\dfrac{cosx}{sinx}}-\dfrac{cos^2x}{1+\dfrac{sinx}{cosx}}=\dfrac{sin^2x}{\dfrac{sinx+cosx}{sinx}}-\dfrac{cos^2x}{\dfrac{cosx+sinx}{cosx}}=\dfrac{sin^3x}{sinx+cosx}-\dfrac{cos^3x}{sinx+cosx}=\dfrac{\left(sinx-cosx\right)\left(sin^2x-sinx\cdot cosx+cos^2x\right)}{sinx+cosx}=\dfrac{\left(sinx-cosx\right)\left(1-sinx\cdot cosx\right)}{sinx+cosx}\)???
Đúng 0
Bình luận (1)
Tính giá trị biểu thức:
M= sin x.cos x + \(\dfrac{sin^2x}{1+cotx}\) + \(\dfrac{cos^2x}{1+tanx}\) với 0độ<x<90độ
\(M=sinx.cosx+\dfrac{sin^2x}{1+cotx}+\dfrac{cos^2x}{1+tanx}\)
\(=sinx.cosx+\dfrac{sin^2x}{\dfrac{cosx+sinx}{sinx}}+\dfrac{cos^2x}{\dfrac{cosx+sinx}{cosx}}\)
\(=sinx.cosx+\dfrac{sin^3x+cos^3x}{cosx+sinx}\)
\(=sinx.cosx+\dfrac{\left(sinx+cosx\right)\left(sin^2x+cos^2x-sinx.cosx\right)}{cosx+sinx}\)
\(=sinx.cosx+sin^2x+cos^2x-sinx.cosx\)
\(=sin^2x+cos^2x=1\)
Đúng 1
Bình luận (0)
Tìm tập xác đinh của các hàm số sau
29 , yfrac{tanx+cosx}{sinx}
30 , yfrac{1}{sinx}-frac{1}{cosx}
31 , yfrac{cosx+cotx}{sinx}
32 , yfrac{tanx+cotx}{1-sin2x}
33 , ytanx+frac{1}{cosfrac{x}{2}}
34 , yfrac{1-tanx}{1-cotx}
35 , yfrac{cotx}{cosx-1}
36 , yfrac{3}{sin^2x-cos^2x}
37 , yfrac{2}{cosx-cos3x}
38 , yfrac{sqrt{x}}{sinpi x}
39 , yfrac{2-cosx}{1+tanleft(x-frac{pi}{3}right)}
Đọc tiếp
Tìm tập xác đinh của các hàm số sau
29 , \(y=\frac{tanx+cosx}{sinx}\)
30 , \(y=\frac{1}{sinx}-\frac{1}{cosx}\)
31 , \(y=\frac{cosx+cotx}{sinx}\)
32 , \(y=\frac{tanx+cotx}{1-sin2x}\)
33 , \(y=tanx+\frac{1}{cos\frac{x}{2}}\)
34 , \(y=\frac{1-tanx}{1-cotx}\)
35 , \(y=\frac{cotx}{cosx-1}\)
36 , \(y=\frac{3}{sin^2x-cos^2x}\)
37 , \(y=\frac{2}{cosx-cos3x}\)
38 , \(y=\frac{\sqrt{x}}{sin\pi x}\)
39 , \(y=\frac{2-cosx}{1+tan\left(x-\frac{\pi}{3}\right)}\)
ĐKXĐ:
29.
\(\left\{{}\begin{matrix}cosx\ne0\\sinx\ne0\end{matrix}\right.\) \(\Leftrightarrow sinx.cosx\ne0\)
\(\Leftrightarrow sin2x\ne0\Leftrightarrow x\ne\frac{k\pi}{2}\)
30.
\(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\end{matrix}\right.\) \(\Leftrightarrow x\ne\frac{k\pi}{2}\) (như câu trên)
31.
\(sinx\ne0\Leftrightarrow x\ne k\pi\)
32.
\(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\\sin2x\ne1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}sin2x\ne0\\sin2x\ne1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\frac{k\pi}{2}\\x\ne\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
33.
\(\left\{{}\begin{matrix}cosx\ne0\\cos\frac{x}{2}\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne\frac{\pi}{2}+k\pi\\x\ne\pi+k2\pi\end{matrix}\right.\)
34.
\(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\\cotx\ne1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}sin2x\ne0\\cotx\ne1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\frac{k\pi}{2}\\x\ne\frac{\pi}{4}+k\pi\end{matrix}\right.\)
35.
\(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne1\end{matrix}\right.\) \(\Leftrightarrow sinx\ne0\)
\(\Leftrightarrow x\ne k\pi\)
Đúng 0
Bình luận (0)
36.
\(sin^2x-cos^2x\ne0\Leftrightarrow cos2x\ne0\)
\(\Leftrightarrow x\ne\frac{\pi}{4}+\frac{k\pi}{2}\)
37.
\(cos3x\ne cosx\Leftrightarrow\left\{{}\begin{matrix}3x\ne x+k2\pi\\3x\ne-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne k\pi\\x\ne\frac{k\pi}{2}\end{matrix}\right.\) \(\Leftrightarrow x\ne\frac{k\pi}{2}\)
38.
\(\left\{{}\begin{matrix}x\ge0\\sin\pi x\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\pi x\ne k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne k\end{matrix}\right.\)
39.
\(\left\{{}\begin{matrix}cos\left(x-\frac{\pi}{3}\right)\ne0\\tan\left(x-\frac{\pi}{3}\right)\ne-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x-\frac{\pi}{3}\ne\frac{\pi}{2}+k\pi\\x-\frac{\pi}{3}\ne-\frac{\pi}{4}+k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\frac{5\pi}{6}+k\pi\\x\ne-\frac{\pi}{12}+k\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)