Mn trả lời nhanh nhanh giùm em với ạ. Em đang cần gấp...

- Ta có: \(\sin\alpha+\cos\alpha=\frac{7}{5}\)  

        \(\Rightarrow\sin\alpha=\frac{7}{5}-\cos\alpha\)

- Theo tỉ số lượng giác của óc nhọn, ta có:

         \(\sin^2\alpha+\cos^2\alpha=1\)

\(\Leftrightarrow\left(\frac{7}{5}-\cos\alpha\right)^2+\cos^2\alpha=1\)

\(\Leftrightarrow\frac{49}{25}-\frac{14}{5}\cos\alpha+\cos^2\alpha+\cos^2\alpha=1\)

\(\Leftrightarrow50\cos^2\alpha-70\cos\alpha+48=0\)

\(\Leftrightarrow25\cos^2\alpha-35\cos\alpha+24=0\)

\(\Leftrightarrow\left(5\cos\alpha-4\right)\left(5\cos\alpha-3\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}5\cos\alpha-4=0\\5\cos\alpha-3=0\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}\cos\alpha=\frac{4}{5}\\\cos\alpha=\frac{3}{5}\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}\sin\alpha=\frac{7}{5}-\cos\alpha=\frac{7}{5}-\frac{4}{5}=\frac{3}{5}\\\sin\alpha=\frac{7}{5}-\cos\alpha=\frac{7}{5}-\frac{3}{5}=\frac{4}{5}\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}\tan\alpha=\frac{\sin\alpha}{\cos\alpha}=\frac{\frac{3}{5}}{\frac{4}{5}}=\frac{3}{4}\\\tan\alpha=\frac{\sin\alpha}{\cos\alpha}=\frac{\frac{4}{5}}{\frac{3}{5}}=\frac{4}{3}\end{cases}}\)

Kết luận: Vậy..........

Tham khảo:

a) 

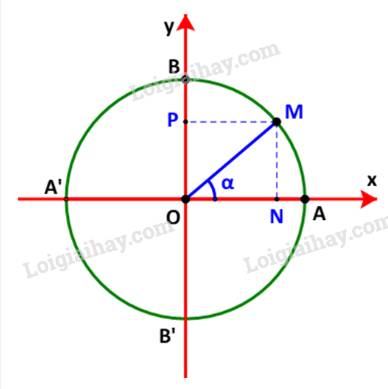
Gọi M(x;y) là điểm trên đường tròn đơn vị sao cho \(\widehat {xOM} = \alpha \). Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.

Ta có: \(\left\{ \begin{array}{l}x = \cos \alpha \\y = \sin \alpha \end{array} \right. \Rightarrow \left\{ \begin{array}{l}{\cos ^2}\alpha  = {x^2}\\{\sin ^2}\alpha  = {y^2}\end{array} \right.\)(1)

Mà \(\left\{ \begin{array}{l}\left| x \right| = ON\\\left| y \right| = OP = MN\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x^2} = {\left| x \right|^2} = O{N^2}\\{y^2} = {\left| y \right|^2} = M{N^2}\end{array} \right.\)(2)

Từ (1) và (2) suy ra \({\sin ^2}\alpha  + {\cos ^2}\alpha  = O{N^2} + M{N^2} = O{M^2}\) (do \(\Delta OMN\) vuông tại N)

\( \Rightarrow {\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\) (vì OM =1). (đpcm)

b) 

Ta có:  \(\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }}\;\;(\alpha  \ne {90^o})\)

\( \Rightarrow 1 + {\tan ^2}\alpha  = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha  + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }}\)

Mà theo ý a) ta có \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\) với mọi góc \(\alpha \)

\( \Rightarrow 1 + {\tan ^2}\alpha  = \frac{1}{{{{\cos }^2}\alpha }}\) (đpcm)

c) 

Ta có:  \(\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }}\;\;\;({0^o} < \alpha  < {180^o})\)

\( \Rightarrow 1 + {\cot ^2}\alpha  = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha  + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }}\)

Mà theo ý a) ta có \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\) với mọi góc \(\alpha \)

\( \Rightarrow 1 + {\cot ^2}\alpha  = \frac{1}{{{{\sin }^2}\alpha }}\) (đpcm)

a) 

Trên nửa đường tròn đơn vị, lấy điểm M sao cho \(\widehat {xOM} = \alpha \)

Gọi H, K lần lượt là các hình chiếu vuông góc của M trên Ox, Oy.

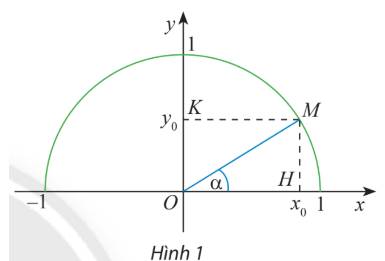
Ta có: tam giác vuông OHM vuông tại H và \(\alpha  = \widehat {xOM}\)

Do đó: \(\sin \alpha  = \frac{{MH}}{{OM}} = MH;\;\cos \alpha  = \frac{{OH}}{{OM}} = OH.\)

\( \Rightarrow {\cos ^2}\alpha  + {\sin ^2}\alpha  = O{H^2} + M{H^2} = O{M^2} = 1\)

b) Ta có:

\(\begin{array}{l}\;\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }}.\\ \Rightarrow \;\tan \alpha .\cot \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\end{array}\)

c) Với \(\alpha  \ne {90^o}\) ta có:

\(\begin{array}{l}\;\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }};\;\\ \Rightarrow \;1 + {\tan ^2}\alpha  = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha  + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\;\end{array}\)

d) Ta có:

\(\begin{array}{l}\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }};\;\\ \Rightarrow \;1 + {\cot ^2}\alpha  = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha  + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\;\end{array}\)

\(P=\dfrac{2sin\alpha-3cos\alpha}{3sin\alpha+2cos\alpha}\\ =\dfrac{\dfrac{2sin\alpha}{cos\alpha}-\dfrac{3cos\alpha}{cos\alpha}}{\dfrac{3sin\alpha}{cos\alpha}+\dfrac{2cos\alpha}{cos\alpha}}\\ =\dfrac{2tan\alpha-3}{3tan\alpha+2}=\dfrac{2.3-3}{3.3+2}=\dfrac{3}{11}\)

Ta có: \(1 + {\tan ^2}\alpha  = \frac{1}{{{{\cos }^2}\alpha }}\quad (\alpha  \ne {90^o})\)

\( \Rightarrow \frac{1}{{{{\cos }^2}\alpha }} = 1 + {3^2} = 10\)

\( \Leftrightarrow {\cos ^2}\alpha  = \frac{1}{{10}} \Leftrightarrow \cos \alpha  =  \pm \frac{{\sqrt {10} }}{{10}}\)

Vì \({0^o} < \alpha  < {180^o}\) nên \(\sin \alpha  > 0\).

Mà \(\tan \alpha  = 3 > 0 \Rightarrow \cos \alpha  > 0 \Rightarrow \cos \alpha  = \frac{{\sqrt {10} }}{{10}}\)

Lại có: \(\sin \alpha  = \cos \alpha .\tan \alpha  = \frac{{\sqrt {10} }}{{10}}.3 = \frac{{3\sqrt {10} }}{{10}}.\)

\( \Rightarrow P = \dfrac{{2.\frac{{3\sqrt {10} }}{{10}} - 3.\frac{{\sqrt {10} }}{{10}}}}{{3.\frac{{3\sqrt {10} }}{{10}} + 2.\frac{{\sqrt {10} }}{{10}}}} = \dfrac{{\frac{{\sqrt {10} }}{{10}}\left( {2.3 - 3} \right)}}{{\frac{{\sqrt {10} }}{{10}}\left( {3.3 + 2} \right)}} = \dfrac{3}{{11}}.\)

Đặt \(\sin\alpha=x,\cos\alpha=y\)

Ta có hpt:

\(\left\{{}\begin{matrix}x+y=\frac{7}{5}\\x^2+y^2=1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x+y=\frac{7}{5}\\xy=\frac{\left(x+y\right)^2-\left(x^2+y^2\right)}{2}=\frac{\left(\frac{7}{5}\right)^2-1}{2}=\frac{12}{25}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=\frac{7}{5}-y\\xy=\frac{12}{25}\end{matrix}\right.\)

\(\Rightarrow xy=y\left(\frac{7}{5}-y\right)=\frac{12}{25}\)

\(\Leftrightarrow\frac{7}{5}y-y^2=\frac{12}{25}\Leftrightarrow y^2-\frac{7}{5}y+\frac{12}{25}=0\)

\(\Delta=\frac{49}{25}-4\cdot\frac{12}{25}=\frac{1}{25}>0;\sqrt{\Delta}=\frac{1}{5}\)

phương trình có 2 nghiệm phân biệt:

\(\left\{{}\begin{matrix}y=\frac{\frac{7}{5}+\frac{1}{5}}{2}=\frac{4}{5}\\y=\frac{\frac{7}{5}-\frac{1}{5}}{2}=\frac{3}{5}\end{matrix}\right.\)

Thay vào tìm x ta được các tập nghiệm: \(\left(x,y\right)=\left(\frac{3}{5};\frac{4}{5}\right);\left(\frac{4}{5};\frac{3}{5}\right)\)

\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\sin\alpha=\frac{3}{5}\\\cos\alpha=\frac{4}{5}\end{matrix}\right.\\\left\{{}\begin{matrix}\sin\alpha=\frac{4}{5}\\\cos\alpha=\frac{3}{5}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\tan\alpha=\frac{\frac{3}{5}}{\frac{4}{5}}=\frac{3}{4}\\\tan\alpha=\frac{\frac{4}{5}}{\frac{3}{5}}=\frac{4}{3}\end{matrix}\right.\)

(Áp dụng \(\tan\alpha=\frac{\sin\alpha}{\cos\alpha}\))

( sin a + cos a )^2 = (7/5)^2 

=> sin^2 a + cos^2a + 2.sina . cos a =  49/25 

=> 1 + 2.sin a . cos a  = 49/25 

=> 2.sin a + cos a = 49/25 - 1 = 24 / 25 

 ( sin a - cos a )^2 = sin ^2 a + cos ^2a  - 2. sin  a . cos a = 1 - 24/25 = 1/25 

=> sin a - cos a = 1/5 (2)

TA có sina + cos a = 7/5 (1)

Từ (1) và (1) => 2 sina = 8/5 => sin a = 8/5 : 2 = 8/10 = 4/5 

=> cos a = sin a - 1/5 = 4/5 - 1/5 = 3/5 

tan a = \(\frac{sina}{cosa}=\frac{\frac{4}{5}}{\frac{3}{5}}=\frac{4}{5}\cdot\frac{5}{3}=\frac{4}{3}\)

a=A          

sin \(\alpha\)- \(\cos\alpha\)=\(\frac{1}{5}\)hoặc \(-\frac{1}{5}\) mới đúng

a, ta có \(\tan\alpha=\frac{\sin\alpha}{\cos\alpha}\)

                  \(\frac{1}{3}\)= \(\frac{\sin\alpha}{\cos\alpha}\)

                    \(\cos\alpha\)= 3 \(\sin\alpha\)

ta có \(\frac{\cos\alpha+\sin\alpha}{\cos\alpha-\sin\alpha}\)= \(\frac{3\sin\alpha+\sin\alpha}{3\sin\alpha-\sin\alpha}\)= \(\frac{4\sin\alpha}{2\sin\alpha}\)= \(2\)

#mã mã#

oh , bác sĩ ơi tui sắp chết

a/ Có \(\tan\alpha=\frac{1}{3}\Rightarrow\frac{\sin\alpha}{\cos\alpha}=\frac{1}{3}\Leftrightarrow\cos\alpha=3\sin\alpha\)

Thay vào biểu thức có:

\(\frac{3\sin\alpha+\sin\alpha}{3\sin\alpha-\sin\alpha}=\frac{4\sin\alpha}{2\sin\alpha}=2\)

b/ Có \(\sin\alpha+\cos\alpha=\frac{7}{5}\Rightarrow\sin\alpha=\frac{7}{5}-\cos\alpha\) (1)

Có \(\sin^2\alpha+\cos^2\alpha=1\) (2)

Thay (1) vào (2) rồi tự thay số vào giải PTB2 để tìm cos và sin

Có \(\tan\alpha=\frac{\sin\alpha}{\cos\alpha}\)

Thay vào là OK