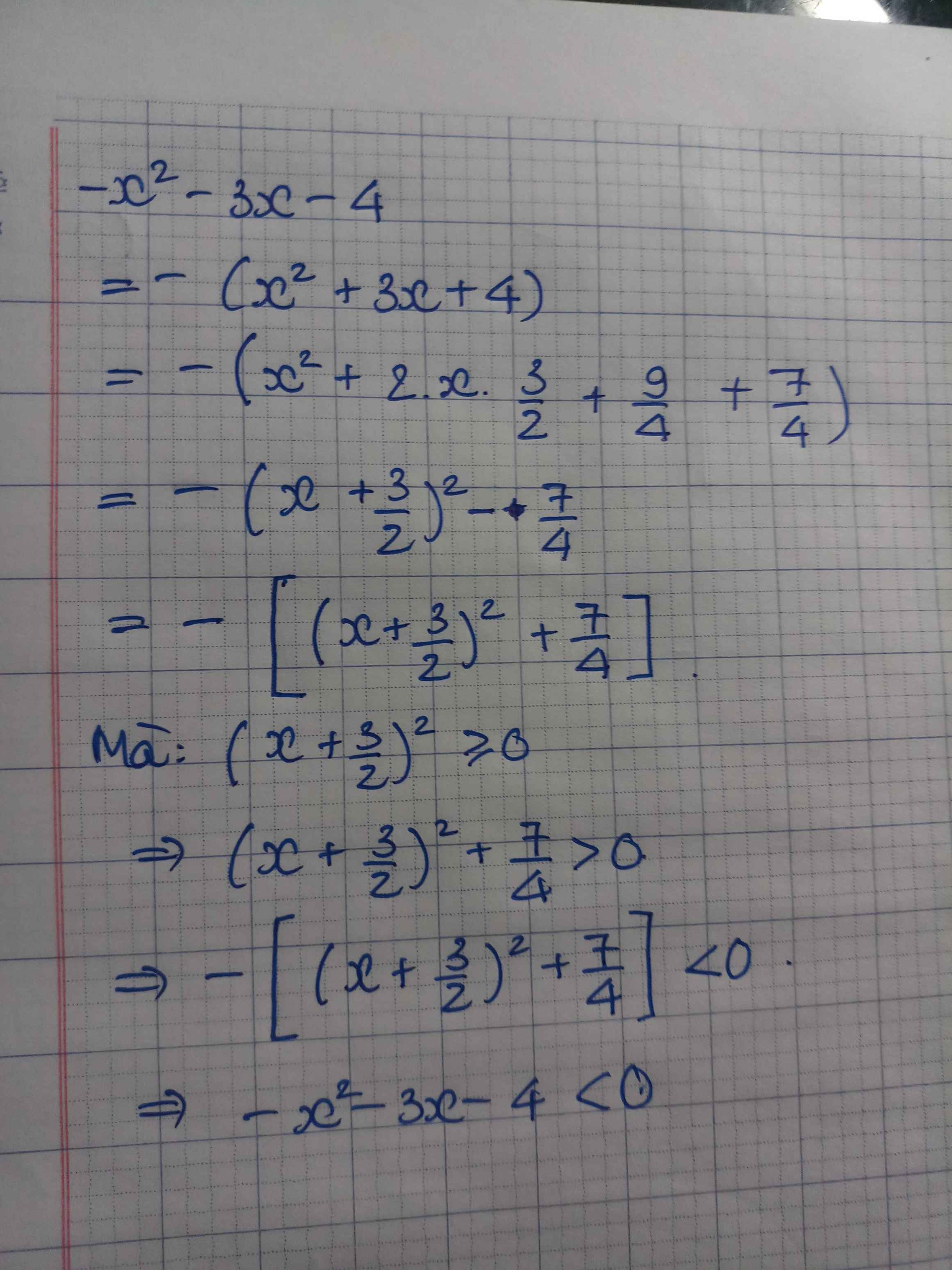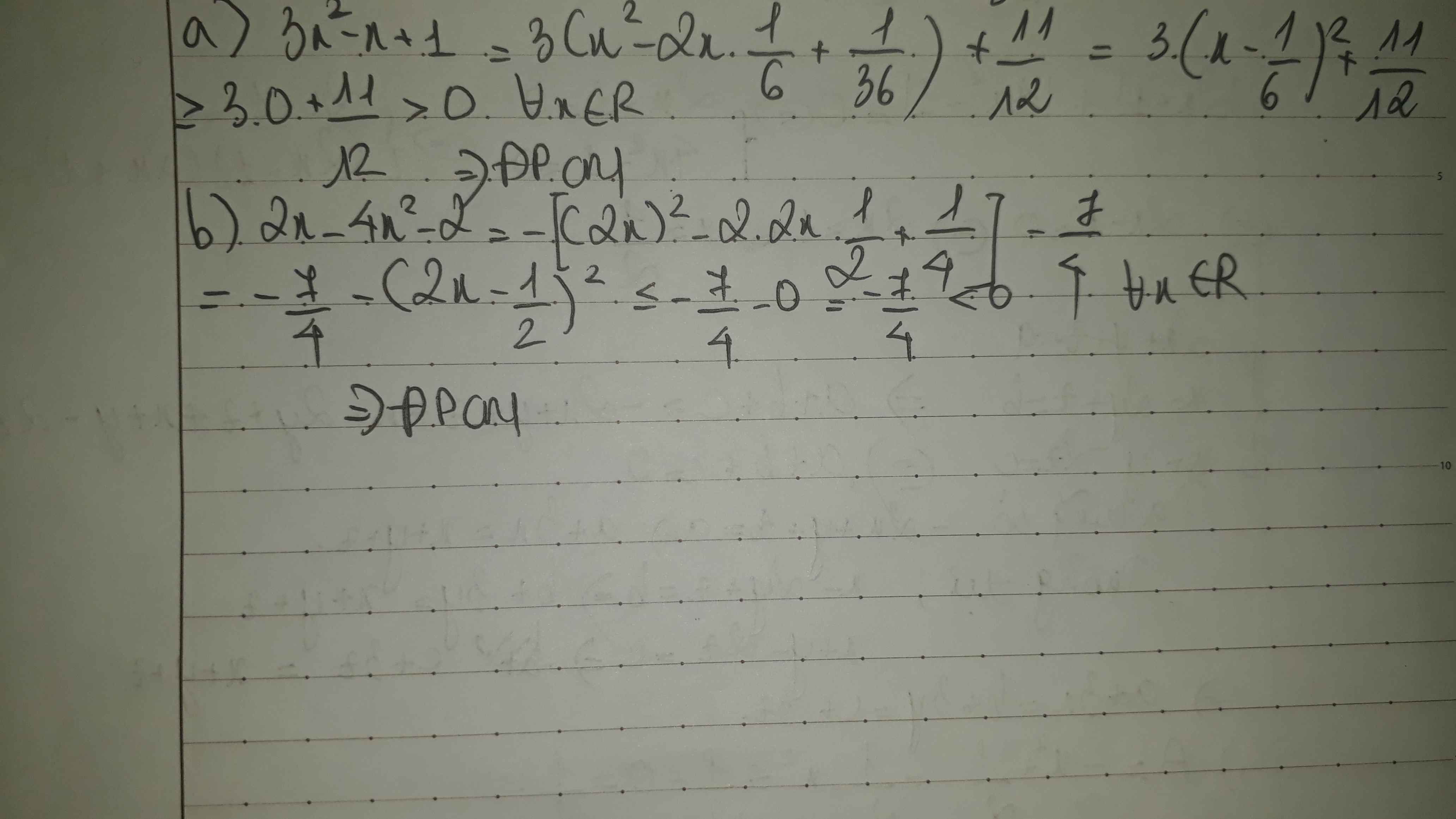chứng minh rằng 3x^2+1>0 với mọi x
CL
Những câu hỏi liên quan
Chứng minh rằng : a, 3x^2+1>0 với mọi x
\(3x^2+1\ge1>0\forall x\)
Đúng 0
Bình luận (0)
chứng minh rằng với mọi x ϵ R
-x^2-3x-4<0
Ta có: \(-x^2-3x-4\)
\(=-\left(x^2+3x+4\right)\)
\(=-\left(x^2+2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{7}{4}\right)\)
\(=-\left(x+\dfrac{3}{2}\right)^2-\dfrac{7}{4}< 0\forall x\)
Đúng 0
Bình luận (0)
1 Chứng minh rằng
a.2x^28x+20>0 với mọi x
b.x^4-3x^2+5>0 với mọi x
c.-x^2+7x-17<0 với mọi x
d.-2x^2+6x^2-5<0 với mọi x
chứng minh rằng với mọi x ϵ R
x^2-8x+17>0
x^2+4x+5>0
x^2-x+1>0
-x^2-4x-5<0
-x^2-3x-4<0
-x^2+10x-27<0
Chứng minh rằng phương trình sau luôn có nghiệm với mọi m:(-X^2+3X-2)m+3X-5=0
\(pt:\left(-x^2+3x-2\right)m+3x-5=0\)
\(\Leftrightarrow-x^2m+3mx-2m+3x-5=0\)
\(\Leftrightarrow-x^2m+\left(3m+3\right)x-2m-5=0\)
pt co nghiem \(\Leftrightarrow\Delta=\left(3m+3\right)^2-4m\left(2m+5\right)\ge0\)
\(\Leftrightarrow9m^2+18m+9-8m^2-20m\ge0\)
\(\Leftrightarrow\left(m-1\right)^2+8>0\left(ld\right)\)
Vay pt luon co nghiem voi moi m
Đúng 0
Bình luận (0)
chứng minh rằng x3+4x+1>3x2 với mọi x lớn hơn bằng 0
1 Chứng minh rằng
a.2x2+8x+20>0 với mọi x
b.x4-3x2+5>0 với mọi x
c.-x2+7x-17<0 với mọi x
d.-2x2+6x2-5<0 với mọi x
a,2x2+8x+20=2(x2+4x)+20
=2(x2+4x+4)+20-4.2
=2(x+2)2+12
Ta có : 2(x+2)2 \(\ge0với\forall x\)
12 > 0
\(\Rightarrow\)2(x+2)2+12>0 với \(\forall x\)
\(\Rightarrow\)2x2+8x+20>0 với \(\forall\)x
b,x4-3x2+5
=(x4-3x2)+5
=(x4-2.\(\frac{3}{2}\)x2+\(\frac{9}{4}\))+5-\(\frac{9}{4}\)
=(x2-\(\frac{3}{2}\))2+\(\frac{11}{4}\)
Có : (x2-3/2)2\(\ge0với\forall x\)
\(\frac{11}{4}\)>0
\(\Rightarrow\)(x2-\(\frac{3}{2}\))2+\(\frac{11}{4}>0với\forall x\)
Đúng 0
Bình luận (0)
chứng minh rằng
a, x2-6x+10>0 với mọi x
b,x2-3x+4>0 với mọi x
c, x2+xy+y2+1>0 với mọi x,y
d, 2x2-2xy+2y2-2x+4y+8>0 với mọi x,y
\(\Leftrightarrow x^2-2.3.x+9+1=\left(x-3\right)^2+1\Rightarrow\hept{\begin{cases}\left(x-3\right)^2\ge0\\1>0\end{cases}}\Rightarrow\left(x-3\right)^2+1>0\)
\(\Leftrightarrow x^2-2.\frac{3}{2}.x+\frac{9}{4}+\frac{7}{4}=\left(x-\frac{3}{2}\right)^2+\frac{7}{4}\Leftrightarrow\hept{\begin{cases}\left(x-\frac{3}{2}\right)^2\ge0\\\frac{7}{4}>0\end{cases}}\Rightarrow\left(x-\frac{3}{2}\right)^2+\frac{7}{4}>0\)
\(\Leftrightarrow2.\left(x^2+xy+y^2+1\right)=x^2+2xy+y^2+x^2+y^2+2=\left(x+y\right)^2+x^2+y^2+2\)
ta có \(\left(x+y\right)^2\ge0,x^2\ge0,y^2\ge0,2>0\Rightarrow\left(x+y\right)^2+x^2+y^2+2>0\)
\(\Leftrightarrow x^2-2xy+y^2+x^2-2.1x+1+y^2+2.2.y+4+3\)\(=\left(x-y\right)^2+\left(x-1\right)^2+\left(y+2\right)^2+3\)
Ta có \(=\left(x-y\right)^2\ge0,\left(x-1\right)^2\ge0,\left(y+2\right)^2\ge0,3>0\)\(\Rightarrow=\left(x-y\right)^2+\left(x-1\right)^2+\left(y+2\right)^2+3>0\)
T i c k cho mình 1 cái nha mới bị trừ 50 đ
Đúng 0
Bình luận (0)
Chứng minh rằng:
a)3x^2-x+1>0 với mọi xϵR
b)2x-4x^2-2<0 với mọi xϵR