
giúp e với gấp lắm rùi ạ!!!!!!!
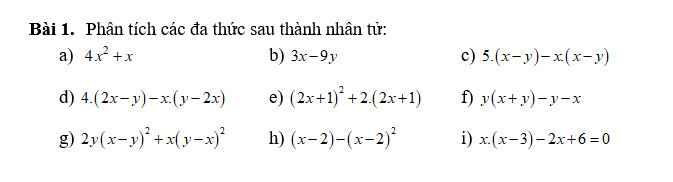
giúp e với ạ gấp lắm rùi ạ:((
a)\(4x^2+x=x\left(4x+1\right)\)
b)\(3x-9y=3\left(x-3y\right)\)
c)\(5\left(x-y\right)-x\left(x-y\right)=\left(5-x\right)\left(x-y\right)\)
d)\(4\left(2x-y\right)-x\left(y-2x\right)=-4\left(y-2x\right)-x\left(y-2x\right)=\left(-4-x\right)\left(y-2x\right)\)
e)\(\left(2x+1\right)^2+2\left(2x+1\right)=\left(2x+1\right)\left(2x+1+2\right)=\left(2x+1\right)\left(2x+3\right)\)
f)\(y\left(x+y\right)-y-x=y\left(x+y\right)-\left(x+y\right)=\left(y-1\right)\left(x+y\right)\)
g)\(2y\left(x-y\right)^2+x\left(y-x\right)^2=2y\left(y-x\right)^2+x\left(y-x\right)^2=\left(2y+x\right)\left(y-x\right)^2\)
h)
h)(x-2)-(x-2)^2=(x-2)(1-x-2)=(x-2)(x-1)
i)x(x-3)-2x+6=x(x-3)-2(x-3)=(x-3)(x-2)
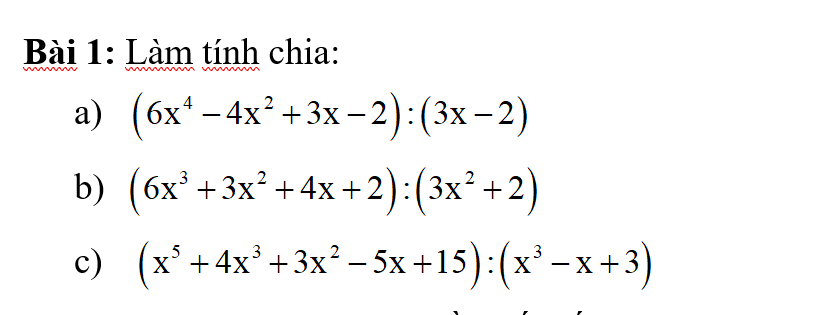
giúp e với ạ! e đg gấp lắm rùi ạ! E cảm ơn
Vậy câu hỏi của bạn đâu
Ai giải giúp mình với mình đang cần gấp lắm ạ mình sắp nộp rùi
Bài 2:
Áp dụng tính chất của dãy tỉ số bằng nhau,ta được
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{45}{9}=5\)
Do đó: a=10; b=15;c=20
Giúp vs, cần gấp lắm rùi ạ😢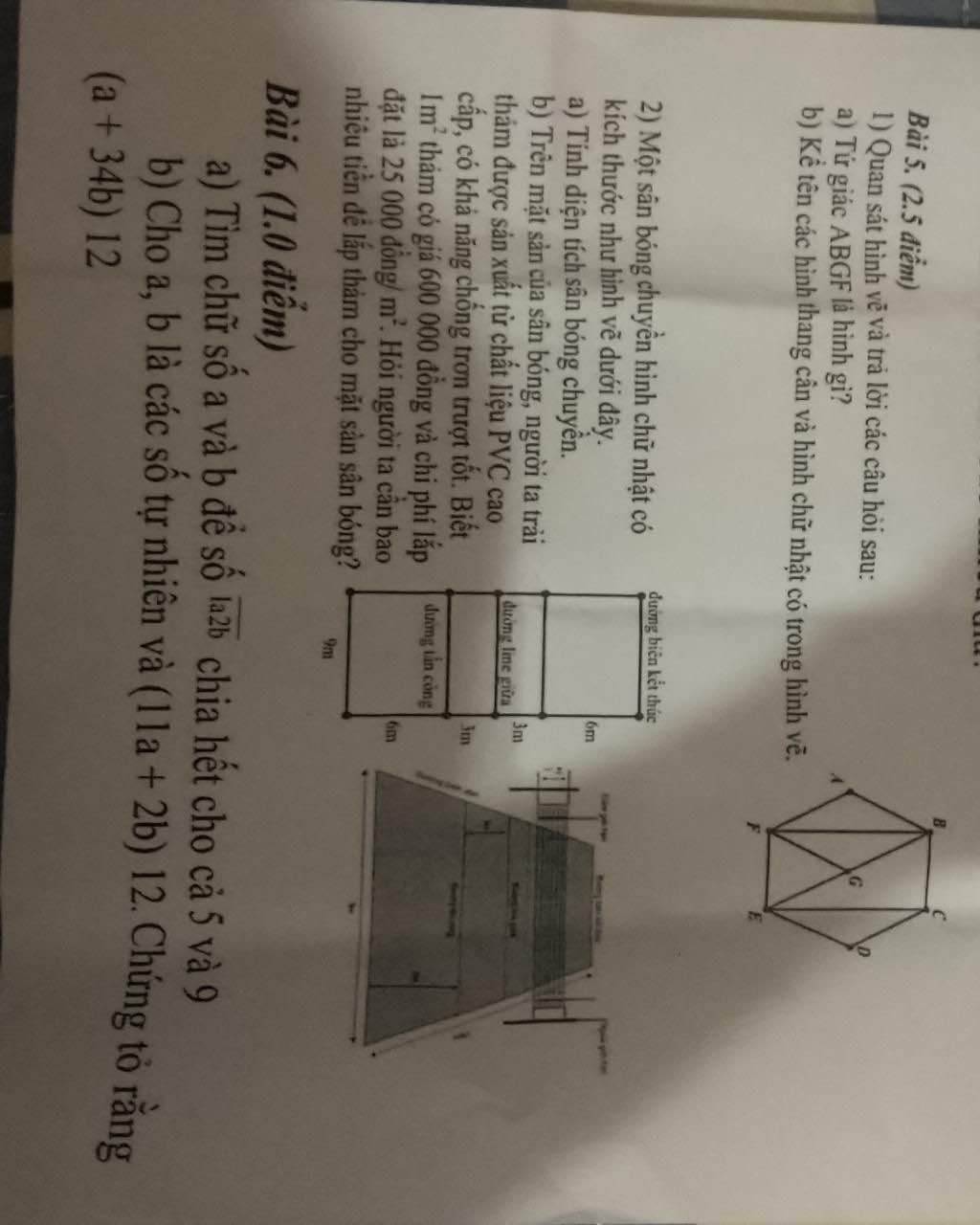

giúp e với ạ, e cần gấp lắm ạ
Giúp e với ạ e cần gấp lắm ạ
1. Why don't we go for picnic on the weekend ?
→ I suggest that we should go for a picnic on the weekend.
2. The weather was awful, but we enjoyed our outdoor party last night
→ Although the weather is awful, we enjoyed our party last night.
3. The music was gentle. We listened to it last night
→ The music, which was gentle, we listened to last night
4. This is Mr. Jones. He writes poetry
→ This is Mr. Jones, who writes poetry

giúp e phần BA ở cuối trang thôi ạ, e cần gấp lắm ạ, giúp e với
Phần BA là phần nào á b mình zoom ảnh thấy phần C
cho biểu thức P =căn x+3/ căn x -1 .với các gt nguyên của x tìm gtnn của P
mọi người giúp e với e cảm ơn mn nhìu lắm
e sắp phải nộp rùi ạ
\(P=\sqrt[]{x}+\dfrac{3}{\sqrt[]{x}-1}\left(x>1\right)\)
\(P=\sqrt[]{x}-1+\dfrac{3}{\sqrt[]{x}-1}+1\)
Áp dụng bất đẳng thức Cauchy cho 2 số \(\sqrt[]{x}-1;\dfrac{3}{\sqrt[]{x}-1}\) ta được :
\(\sqrt[]{x}-1+\dfrac{3}{\sqrt[]{x}-1}\ge2\sqrt[]{\sqrt[]{x}-1.\dfrac{3}{\sqrt[]{x}-1}}\)
\(\Rightarrow\sqrt[]{x}-1+\dfrac{3}{\sqrt[]{x}-1}\ge2\sqrt[]{3}\)
\(\Rightarrow P=\sqrt[]{x}-1+\dfrac{3}{\sqrt[]{x}-1}+1\ge2\sqrt[]{3}+1\)
\(\Rightarrow Min\left(P\right)=2\sqrt[]{3}+1\)
sorry mn cho e sửa lại đề ạ
tìm gtln của p ạ