Cho 5 điểm A,B,C,D,E.Làm sao cho C ở giữa 2 đường thẳng AE và BD (bằng 4 cách)
HM
Những câu hỏi liên quan
cho đoạn AB và một điểm C nằm giữa A và B sao cho AC < CB. Vẽ một tia Cx vuông góc với AB. Trên tia Cx lấy hai điểm D và E sao cho CD bằng CA và CE bằng CB
a) C/m : AE bằng BD
b) C/m: đường thẳng AE vuông góc với đường thẳng BD
Cho 2 điểm E và C trên đường thẳng d sao cho chúng cách nhau 10cm A là trung điểm của EC . Điểm B thuộc tia AE sao cho AB =2cm a) Tính độ dài đoạn thẳng BE b) Tính độ dài đoạn thẳng BC C) điểm D nằm giữa 2 điểm A và C sao cho CD =4cm.Chứng tỏ rằng B là trung điểm của DE
a: AE=AC=10/2=5cm
BE+AB=AE
=>BE=3cm
b: BC=2+5=7cm
c: DE=10-4=6cm
BE và BD là hai tia đối nhau
=>B nằm giữa E và D
mà EB=1/2*ED
nên B là trung điểm của ED
Đúng 0
Bình luận (0)
Trên một đường thẳng cho 4 điểm A,B,C,D sao cho C nằm giữa A và B, còn B nằm giữa C và D . Cho biết AB = 5 cm, AD = 8cm,BC=2cm
a/ Chứng tỏ AC=BD
b/So sánh hai đoạn thẳng AB và BD
Cho tam giác ABC ( AB > AC). Trên đường thẳng chứa cạnh BC, lấy điểm D và điểm E sao cho B nằm giữa D và C, C nằm giữa B và E, BD = BA, CE = CA ( H.9.52)
a) So sánh \(\widehat {ADE}\) và \(\widehat {AED}\).
b) So sánh các đoạn thẳng AD và AE.
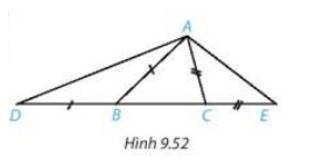
a)
\(AB > AC \Rightarrow \widehat {ABC} < \widehat {ACB}\)( quan hệ giữa góc và cạnh đối diện trong tam giác ABC)
\(\begin{array}{l} \Rightarrow {180^0} - \widehat {ABD} < {180^0} - \widehat {ACE}\\ \Rightarrow \widehat {ABD} > \widehat {ACE}\end{array}\)
Vì BD= BA nên tam giác ABD cân tại B \( \Rightarrow \widehat {ABD} = {180^0} - 2\widehat {ADB}\)
Vì CE = CA nên tam giác ACE cân tại C \( \Rightarrow \widehat {ACE} = {180^0} - 2\widehat {AEC}\)
\(\begin{array}{*{20}{l}}{ \Rightarrow {{180}^0} - 2\widehat {ADB} > {{180}^0} - 2\widehat {AEC}}\\{ \Rightarrow \widehat {ADB} < \widehat {AEC}}\\{Hay{\mkern 1mu} \widehat {ADE} < \widehat {AED}}\end{array}\)
b) Xét tam giác ADE ta có : \(\widehat {ADB} < \widehat {AEC}\)
\( \Rightarrow AD > AE\)(Quan hệ giữa cạnh và góc đối diện trong tam giác).
Đúng 0
Bình luận (0)
Cho đoạn thẳng AB bằng 15 cm lấy điểm C thuộc đoạn thẳng AB sao cho AC = 10 cm và D thuộc đường thang AB sao cho BD = 7cm
a) tinh do dai doan CD
b) Chứng tỏ điểm D nằm giữa hai điểm A, C và điểm C nằm giữa hai điểm A, B
A_____________________D_______C_________________B
a)D thuộc AB mà AB<BD (15cm<7CM)
=> D nằm giữa A và B
=>AD+DB=AB
=>AD+7=15
=>AD=8 cm
vì A;C;D thẳng hàng mà AC>AD(10cm>8cm)
=> D nằm giữa A và C (điều phải chứng mik ở b)
=>AD+CD=AC
=>8+CD=10
=>CD=2 cm
b)mik đã chứng mik ở phần a rồi nhá !
còn C nằm giữa A và B nữa !
vì A ;B;C thẳng hàng
mà AC<AB(10cm<15cm)
=>C nằm giữ A và B
Đúng 1
Bình luận (0)
Trên một đường thẳng cho 4 điểm ABCD sao cho C nằm giữa A và B nằm giữa C và B biết AB = 5 cm, AD = 8 cm, BC = 2 cm
a, Chứng tỏ rằng AC = BD
b, So sánh đoạn thẳng AB và BD
Trên một đường thẳng cho 4 điểm ABCD sao cho D nằm giữa A và B nằm giữa C và B biết AB = 5 cm, AD = 8 cm, BC = 2 cm
a, Chứng tỏ rằng AC = BD
b, So sánh đoạn thẳng AB và BD
ĐỀ THẾ NÀY HẢ
Đúng 0
Bình luận (0)
1.Cho ddt AB và điểm C nằm giữa A và B. Trên cùng một nửa p bờ AB vẽ 2 tam giác đều. ACD và BCE. Gọi M và N lần lượt là trung điểm AE và BD. Chứng minh rằng:a. AE BDb. Tam giác CME tam giác CNB c. MNC là tam giác đều2. Cho tam giác ABC vuông ở A. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD AE. Các đường vuông góc kẻ từ A và E với CD cắt BC ở G và H. Đường thẳng EH và đt AB cắt nhau ở M. Đường thẳng kẻ từ A song song BC cắt MH ở I Chứng minh:a. Tam giác ACD tam giác AMEb. Tam gi...
Đọc tiếp
1.Cho ddt AB và điểm C nằm giữa A và B. Trên cùng một nửa p bờ AB vẽ 2 tam giác đều. ACD và BCE. Gọi M và N lần lượt là trung điểm AE và BD. Chứng minh rằng:
a. AE = BD
b. Tam giác CME = tam giác CNB
c. MNC là tam giác đều
2. Cho tam giác ABC vuông ở A. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD= AE. Các đường vuông góc kẻ từ A và E với CD cắt BC ở G và H. Đường thẳng EH và đt AB cắt nhau ở M. Đường thẳng kẻ từ A song song BC cắt MH ở I
Chứng minh:
a. Tam giác ACD= tam giác AME
b. Tam giác AGB = tam giác MIA
c. BG = GH
Bài 1: 1) Trên tia Ax lấy các điểm B, C, D theo thứ tự đó đó sao cho cho: AB 2 cm, BC 4 cm và CD 8 cm.a) Tính các tỷ số số AB/ BC và BC/CDb) Chứng minh BC2 AB.CD2) Trên đường thẳng d , lấy 4 điểm A, B, C, D theo thứ tự đó sao cho cho AB/BC 3/5, BC/CD 5/6.a) Tính tỉ số AB/CDb) Cho biết AD 28 cm. Tính độ dài các đoạn thẳng AB, BC và CD Bài 2: Cho tam giác ABC và các điểm D, E lần lượt nằm trên hai cạnh AB, AC sao cho AD/AB AE/AC.a) Chứng minh AD/BD AE/ECb) Cho biết AD 2 cm, BD 1 cm và...
Đọc tiếp
Bài 1: 1) Trên tia Ax lấy các điểm B, C, D theo thứ tự đó đó sao cho cho: AB = 2 cm, BC = 4 cm và CD = 8 cm.
a) Tính các tỷ số số AB/ BC và BC/CD
b) Chứng minh BC2 = AB.CD
2) Trên đường thẳng d , lấy 4 điểm A, B, C, D theo thứ tự đó sao cho cho AB/BC = 3/5, BC/CD = 5/6.
a) Tính tỉ số AB/CD
b) Cho biết AD = 28 cm. Tính độ dài các đoạn thẳng AB, BC và CD
Bài 2: Cho tam giác ABC và các điểm D, E lần lượt nằm trên hai cạnh AB, AC sao cho AD/AB = AE/AC.
a) Chứng minh AD/BD = AE/EC
b) Cho biết AD = 2 cm, BD =1 cm và AE = 4 cm. Tính AC.
Bài 3: Cho tam giác ABC có D, E lần lượt thuộc các cạnh AB và AC sao cho BD/AB = CE/CA.
a) Chứng minh AD/AB = AE/AC
b) Cho biết AD = 2 cm, BD = 1 cm và AC = 4 cm. Tính EC
Bài 4: Cho tam giác ACE có AC = 11 cm. Lấy điểm B trên cạnh AC sao cho BC = 6cm. Lấy điểm D trên cạnh AE sao cho BD song song với EC. Giả sử AE + ED = 25,5 cm. Hãy tính:
a) Tỷ số DE/AE
b) Độ dài các đoạn thẳng AE, DE và AD.
Bài 5: Cho tam giác ABC và điểm D trên cạnh BC sao cho BD/BC = 3/4, điểm E trên đoạn thẳng AD sao cho cho AE/AD = 1/3. Gọi K là giao điểm của BE và AC. a) Tính tỷ số số AK/KC
b) Vẽ hình bình hành ABCM. Trên cạnh MC lấy điểm G sao cho MG= 1/4 MC. Gọi N là giao điểm của AG và BM. Tính tỉ số MN/MB.
Cho tứ diện ABCD có ACADBCBD, ABa, CD
a
3
Khoảng cách giữa hai đường thẳng AB và CD bằng a . Tính khoảng cách h từ điểm cách đều 4 đỉnh A,B,C,D đến mỗi đỉnh đó A.
h
a
13
2
B.
h
a
13
4
C.
h
a...
Đọc tiếp
Cho tứ diện ABCD có AC=AD=BC=BD, AB=a, CD= a 3 Khoảng cách giữa hai đường thẳng AB và CD bằng a . Tính khoảng cách h từ điểm cách đều 4 đỉnh A,B,C,D đến mỗi đỉnh đó
A. h = a 13 2
B. h = a 13 4
C. h = a 3 2
D. h = a 3 4



