Lời giải

Ta có

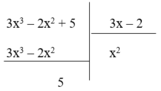
Vì phần dư R = 5 ≠ 0 nên phép chia đa thức 3 x 3   –   2 x 2 + 5 cho đa thức 3x – 2 là phép chia có dư. Do đó (I) sai

Lại có

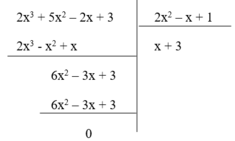
Nhận thấy phần dư R = 0 nên phép chia đa thức ( 2 x 3   +   5 x 2 – 2x + 3) cho đa thức (2 x 2 – x + 1) là phép chia hết. Do đó (II) đúng

Đáp án cần chọn là: D

Bài 1: 

a: \(=\dfrac{2x^4-8x^3+2x^2+2x^3-8x^2+2x+18x^2-72x+18+56x-15}{x^2-4x+1}\)

\(=2x^2+2x+18+\dfrac{56x-15}{x^2-4x+1}\)

b: Ta có: f(x):g(x)

\(=\dfrac{x^3-2x^2+3x+a}{x+1}\)

\(=\dfrac{x^3+x^2-3x^2-3x+6x+6+a-6}{x+1}\)

\(=x^2-3x+6+\dfrac{a-6}{x+1}\)

Để f(x):g(x) là phép chia hết thì a-6=0

hay a=6

a: Thay a=3 vào f(x), ta được:

\(f\left(x\right)=x^3-2x^2+3x+3\)

\(\dfrac{f\left(x\right)}{g\left(x\right)}=\dfrac{x^3-2x^2+3x+3}{x+1}\)

\(=\dfrac{x^3+x^2-3x^2-3x+6x+6-3}{x+1}\)

\(=x^2-3x+6-\dfrac{3}{x+1}\)

1: Sửa đề: 3x-5

\(=\dfrac{-x^2\left(3x-5\right)-3\left(3x-5\right)}{3x-5}=-x^2-3\)

2: \(=\dfrac{5x^4-5x^3+14x^3-14x^2+12x^2-12x+8x-8}{x-1}\)

=5x^2+14x^2+12x+8

3: \(=\dfrac{5x^3+10x^2+4x^2+8x+4x+8}{x+2}=5x^2+4x+4\)

4: \(=\dfrac{\left(x^2-1\right)\left(x^2+1\right)-2x\left(x^2-1\right)}{x^2-1}=x^2+1-2x\)

5: \(=\dfrac{x^2\left(5-3x\right)+3\left(5-3x\right)}{5-3x}=x^2+3\)

a) \(\left(5x^2-2x+1\right)\left(2x^2-3x\right)\)

\(=10x^4-15x^3-4x^3+6x^2+2x^2-3x\)

\(=10x^4-19x^3+8x^2-3x\)

b) \(\left(18x^4y^3-6x^2y^3+12x^3y^4z\right)\)

\(=6x^2y^3\left(3x^2-1+2xyz\right)\)

\(\Rightarrow\left(18x^4y^3-6x^2y^3+12x^3y^4z\right):6x^2y^3\)

\(=\left[6x^2y^3\left(3x^2-1+2xyz\right)\right]:6x^2y^3\)

\(=3x^2+2xyz-1\)

c) \(\left(6x^3-7x^2-x+1\right)\)

\(=3x^2\left(2x+1\right)-5x\left(2x+1\right)+2\left(2x+1\right)-1\)

\(=\left(2x+1\right)\left(3x^2-5x+2\right)-1\)

\(\Rightarrow\left(6x^3-7x^2-x+1\right):\left(2x+1\right)\)

\(=\left[\left(2x+1\right)\left(3x^2-5x+1\right)-1\right]:\left(2x+1\right)\)

\(=3x^2-5x+1\) (Dư \(-1\))

a)(5x²-2x+1).(2x²-3x)

=10x⁴-4x³+2x²-15x³+6x²-3x

=10x⁴-19x³+8x²-3x

b)(18x⁴y³-6x²y³+12x³y⁴z):6x²y³

=(18x⁴y³:6x²y³)-(6x²y³:6x²y³)+(12x³y⁴z:6x²y³)

=3x²y-xy+2xyz

Bài 1:

Ta có: \(5x^3-3x^2+2x+a⋮x+1\)

\(\Leftrightarrow5x^3+5x^2-8x^2-8x+10x+10+a-10⋮x+1\)

\(\Leftrightarrow a-10=0\)

hay a=10