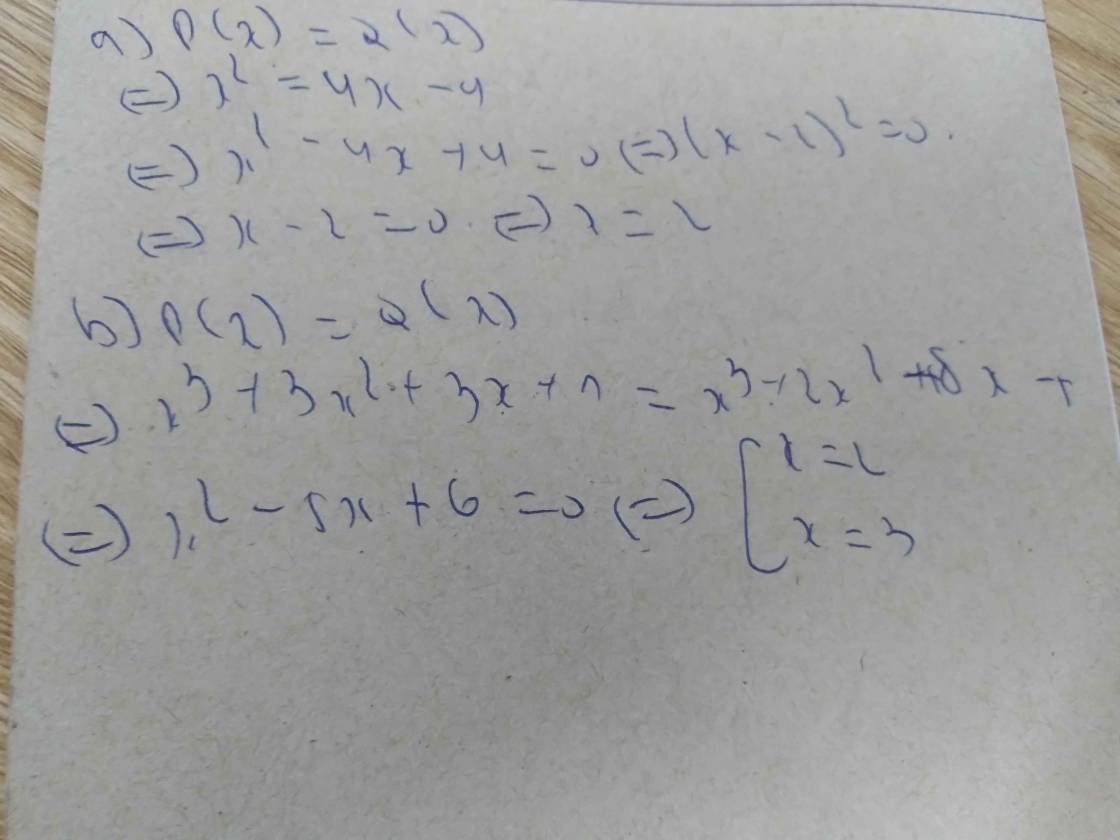cho đa thức A(x)=x^2+px+q , B(x)=x^2-3x-4 Tìm p,q biết A(x)=B(x) với mọi x
TD
Những câu hỏi liên quan
Cho đa thức f(x)=\(^{x^4-3x^3+3x^2+ax+b.}Với\)giá trị nào của a và b thì đa thức f(x)luân chia hết cho đa thức g(x)=\(x^2-3x+4\)với mọi x
Các số nguyên p,q phải thoả mãn điều kiện gì để:
a) Đa thức P(x)=x^2+px+q có giá trị là số chẵn với mọi x thuộc Z
b) Đa thức Q(x)=x^3+px+q có giá trị là bội của 3 với mọi x thuộc Z
a, để p(x) là số chẵn với mọi x thuộc z thì:
p(0)=q là số chẵn
p(1)=1^2+p*1+q là số chẵn
Mà q là số chẵn nên 1+p là số chẵn
suy ra p là số lẻ
suy ra nếu q là số chẵn, p là số lẻ thì p(x)là số chẵn với mọi x thuộc z
Đúng 0
Bình luận (0)
Cho 2 đa thức P(x)=2x^2+3x-5 và Q(x)=2x^2-7x+5
a, Tính A(x)=P(x)+Q(x) : B(x)=P(x)-Q(x)
b, Tìm nghiệm của đa thức A(x) và B(x) (giúp với)
\(a,A\left(x\right)=P\left(x\right)+Q\left(x\right)=2x^2+3x-5+2x^2-7x+5\\ =\left(2x^2+2x^2\right)+\left(3x-7x\right)+\left(-5+5\right)\\ =4x^2-4x\\ B\left(x\right)=P\left(x\right)-Q\left(x\right)=2x^2+3x-5-\left(2x^2-7x+5\right)\\ =2x^2+3x-5-2x^2+7x-5\\ =\left(2x^2-2x^2\right)+\left(3x+7x\right)+\left(-5-5\right)\\ =4x-10\)
b, \(A\left(x\right)=0\\ \Rightarrow4x^2-4x=0\\\Leftrightarrow 4x\left(x-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}4x=0\\x-1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy nghiệm của A(x) là 0 và 1
\(B\left(x\right)=0\\ 4x-10=0\\ \Leftrightarrow4x=10\\ \Leftrightarrow x=\dfrac{5}{2}\)
Vậy nghiệm của B(x) là \(\dfrac{5}{2}\)
Đúng 2
Bình luận (0)
giúp với ạ
cho đa thức :A(x)=x^4-4x^3+2x^2-5x+6.
a, tính giá trị đa thức A(x) biết |4x-1|=1 .
b, tìm đa thức B(x) biết : a(x) -b(x) = 3x^2-x-3x^3-x^2+x^4-2x^2+6 .
c, tìm nghiêm đa thức B(x)
Cho các đa thức P(x) = 2x^2 - 3x -4. Q(x) = x^2 - 3x + 5 a) Tính giá trị của đa thức P(x) tại x =1 b) Tìm H(x) =P(x) - Q(x) c)Tìm nghiệm của đa thức H(x)
a, \(P\left(1\right)=2-3-4=-5\)
b, \(H\left(x\right)=P\left(x\right)-Q\left(x\right)=x^2-9\)
c, Ta có \(H\left(x\right)=\left(x-3\right)\left(x+3\right)=0\Leftrightarrow x=3;x=-3\)
Đúng 1
Bình luận (0)
1. Xác định các đa thức sau:a) Nhị thức bậc nhất f(x) ax + b với a≠0, biết f(-1) 1 và f(1) -1b) Tam thức bậc hai gleft(xright)ax^2+bx+c với a≠0, biết g(-2) 9, g(-1) 2, g(1)62.a) Đa thức f(x) ax + b (a≠0). Biết f(0) 0. Chứng minh f(x) -f(-x) với mọi x b) Đa thức f(x) ax2 + bx + c (a≠0). Biết f(1) f(-1). Chứng minh f(x) f(-x) với mọi x.3. Tìm tổng các hệ số của đa thức sau khi phá ngoặc và sắp xếp, biết:a) Đa thức fleft(xright)left(2x^3-3x^2+2x+1right)^{10}b) Đa thức gleft(xright)left...
Đọc tiếp
1. Xác định các đa thức sau:
a) Nhị thức bậc nhất f(x) = ax + b với a≠0, biết f(-1) = 1 và f(1) = -1
b) Tam thức bậc hai \(g\left(x\right)=ax^2+bx+c\) với a≠0, biết g(-2) = 9, g(-1) = 2, g(1)=6
2.a) Đa thức f(x) = ax + b (a≠0). Biết f(0) = 0. Chứng minh f(x) = -f(-x) với mọi x
b) Đa thức f(x) = ax2 + bx + c (a≠0). Biết f(1) = f(-1). Chứng minh f(x) = f(-x) với mọi x.
3. Tìm tổng các hệ số của đa thức sau khi phá ngoặc và sắp xếp, biết:
a) Đa thức \(f\left(x\right)=\left(2x^3-3x^2+2x+1\right)^{10}\)
b) Đa thức \(g\left(x\right)=\left(3x^2-11x+9\right)^{2011}.\left(5x^4+4x^3+3x^2-12x-1\right)^{2012}\)
1.a) Theo đề bài,ta có: \(f\left(-1\right)=1\Rightarrow-a+b=1\)
và \(f\left(1\right)=-1\Rightarrow a+b=-1\)
Cộng theo vế suy ra: \(2b=0\Rightarrow b=0\)
Khi đó: \(f\left(-1\right)=1=-a\Rightarrow a=-1\)
Suy ra \(ax+b=-x+b\)
Vậy ...
Đúng 0
Bình luận (0)
Tớ nêu hướng giải bài 3 thôi nhé:
Bài toán: Cho đa thức \(f\left(x\right)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0\)
Chứng minh tổng các hệ số của đa thức f(x) là giá trị của đa thức khi x = 1
Lời giải:
Thật vậy,thay x = 1 vào:
\(f\left(1\right)=a_n+a_{n-1}+...+a_1+a_0\) (đúng bằng tổng các hệ số của đa thức)
Vậy tổng các hệ số của 1 đa thức chính là giá trị của đa thức đó khi x = 1 (đpcm)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tìm x
5x(x^3)x^2-5(x-1)^3+15(x-4)(x+4)=5
2)Cho A,B,Q là các đa thức
Biết A=2x^3-x^2+5x-12;B=2x-3
a)Tìm Q
b)C/Minh rằng Q>0 với mọi x
c)Tìm x để Q đạt gtnn
cho đa thức p(x)= -3x^2+x+7/4 và Q(x)= -3x^2+2x-2 a, Tính P(-1) và P(-1/2) b, tìm nghiệm của đa thức P(x)-Q(x)
a) _P(-1)= -3.(-1)^2 + (-1) + 7/4
= -3+(-1)+1,75
=-4+1,75
=-2,25
_P(-1/2)=-3.(-1/2)^2+(-1/2)+7/4
=-3.1/4+(-1/2)+7/4
=-3/4+(-2/4)+7/4
=-5/4+7/4
=2/4=1/2
b) P(x)=-3x^2+x+7/4
-
Q(x)=-3x^2+2x-2
P(x)-Q(x)= -x+3,75
Xet -x+3,75=0
-x =0-3,75
-x =-3,75
=> x =3,75
Vay nghiem cua da thuc P(x)-Q(x) la:3,75
Đúng 1
Bình luận (0)
a) cho 2 đa thức P(x)=x2 và đa thức Q(x)=4x-4. với giá trị nào của x thì P(x)=Q(x)
b) a) cho 2 đa thức P(x)=x3+3x2+3x+1 và đa thức Q(x)=x3+2x2+8x-5. với giá trị nào của x thì P(x)=Q(x)