a, \(x^2\) + 4\(x\) + 10

= ( \(x^2\) + 4\(x\) + 4) + 6

= (\(x\) + 2)² + 6

vì (\(x\) + 2)² ≥ 0 

⇒ (\(x\) + 2)² + 6 ≥ 6 > 0 vậy đa thức đã cho vô nghiệm (đpcm)

b, \(x^2\) - 2\(x\) + 5

= (\(x^2\) - 2\(x\) + 1) + 4 

= (\(x\) - 1)² + 4

Vì (\(x\) - 1)² ≥ 0 ⇒ (\(x\) -1)² + 4≥ 4 > 0

Vậy đa thức đã cho vô nghiệm (đpcm)

a, Cho \(x^2+2022x=0\Leftrightarrow x\left(x+2022\right)=0\Leftrightarrow x=0;x=-2022\)

b, \(3x^2+7x+4=0\Leftrightarrow\left(x+1\right)\left(3x+4\right)=0\Leftrightarrow x=-1;x=-\dfrac{4}{3}\)

c, \(2\left(x^2+2x+1-1\right)+5=0\Leftrightarrow2\left(x+1\right)^2+3=0\)(vô lí) 

Vậy đa thức ko có nghiệm tm 

Bài 1:
1. 

$6x^3-2x^2=0$

$2x^2(3x-1)=0$

$\Rightarrow 2x^2=0$ hoặc $3x-1=0$

$\Rightarrow x=0$ hoặc $x=\frac{1}{3}$
Đây chính là 2 nghiệm của đa thức

2.

$|3x+7|\geq 0$

$|2x^2-2|\geq 0$

Để tổng 2 số bằng $0$ thì: $|3x+7|=|2x^2-2|=0$

$\Rightarrow x=\frac{-7}{3}$ và $x=\pm 1$ (vô lý) 

Vậy đa thức vô nghiệm.

Bài 2:

1. $x^2+2x+4=(x^2+2x+1)+3=(x+1)^2+3$

Do $(x+1)^2\geq 0$ với mọi $x$ nên $x^2+2x+4=(x+1)^2+3\geq 3>0$ với mọi $x$
$\Rightarrow x^2+2x+4\neq 0$ với mọi $x$

Do đó đa thức vô nghiệm

2.

$3x^2-x+5=2x^2+(x^2-x+\frac{1}{4})+\frac{19}{4}$

$=2x^2+(x-\frac{1}{2})^2+\frac{19}{4}\geq 0+0+\frac{19}{4}>0$ với mọi $x$

Vậy đa thức khác 0 với mọi $x$

Do đó đa thức không có nghiệm.

Bài 3:

$f(0)=a.0^3+b.0^2+c.0+d=d=5$

$f(1)=a+b+c+d=4$

$a+b+c=4-d=-1(*)$
$f(2)=8a+4b+2c+d=31$

$8a+4b+2c=31-d=26$

$4a+2b+c=13(**)$
$f(3)=27a+9b+3c+d=88$
$27a+9b+3c=88-d=83(***)$

Từ $(*); (**); (***)$ suy ra $a=\frac{1}{3}; b=13; c=\frac{-43}{3}$

Vậy.......

Cho A(x) = 0, có:

x² - 4x = 0

=> x (x - 4) = 0

=> x = 0 hay x - 4 = 0

=> x = 0 hay x = 4

Vậy: x = 0; x = 4 là nghiệm của đa thức A(x)

a: \(P\left(1\right)=1^3-1^2-4\cdot1+4=-4+4=0\)

=>x=1 là nghiệm của P(x)

\(P\left(-2\right)=\left(-2\right)^3-\left(-2\right)^2-4\cdot\left(-2\right)+4=-8-4+8+4=0\)

=>x=-2 là nghiệm của P(x)

b: \(P\left(1\right)=5\cdot1^3-7\cdot1^2+4\cdot1-2=5-7+4-2=0\)

=>x=1 là nghiệm của P(x)

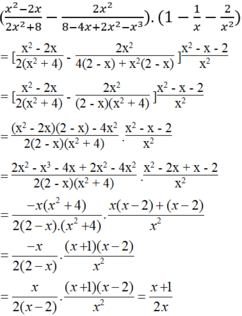
Vế trái bằng vế phải nên đẳng thức được chứng minh.

a) x³+4x-5 = x³-x²+x²+4x-5=(x³-x²)+(x²-x)+(5x-5)=x²(x-1)+x(x-1)+5(x-1)=(x²+x+5)(x-1)

b) x³-3x²+4=x³-2x²-x²+4=(x³-2x²)-(x²-4)=x²(x-2)-(x-2)(x+2)=(x²-x+2)(x-2)

c) x³+2x²+3x+2=x³+x²+x²+x+2x+2=(x³+x²)+(x²+x)+(2x+2)=x²(x+1)+x(x+1)+2(x+1)=(x²+x+2)(x+1)

d) bạn xem lại đề đúng ko

e) (x²+3x)²-2(x²+3x)-8=x⁴+6x³+9x²-2x²-6x-8=x⁴+6x³+7x²-6x-8=x⁴-x³+7x³-7x²+14x²-14x+8x-8=(x⁴-x³)+(7x³-7x²)+(14x²-14x)+(8x-8)=x³(x-1)+7x²(x-1)+14x(x-1)+8(x-1)=(x³+7x²+14x+8)(x-1)=(x³+x²+6x²+6x+8x+8)(x-1)=\(\left[\left(x^3+x^2\right)+\left(6x^2+6x\right)+\left(8x+8\right)\right]\left(x-1\right)\)\(=\left[x^2\left(x+1\right)+6x\left(x+1\right)+8\left(x+1\right)\right]\left(x-1\right)\)\(=\left(x^2+6x+8\right)\left(x+1\right)\left(x-1\right)\)\(=\left(x^2+2x+4x+8\right)\left(x+1\right)\left(x-1\right)\)\(=\left[\left(x^2+2x\right)+\left(4x+8\right)\right]\left(x+1\right)\left(x-1\right)\)\(=\left[x\left(x+2\right)+4\left(x+2\right)\right]\left(x+1\right)\left(x-1\right)\)=\(\left(x-1\right)\left(x+1\right)\left(x+2\right)\left(x+4\right)\)

f) (x²+4x+10)²-7(x²+4x+11)+7=(x²+4x+10)²-\(\left[7\left(x^2+4x+11\right)-7\right]\)\(=\left(x^2+4x+10\right)^2-7\left(x^2+4x+10\right)\)\(=\left(x^2+4x+10\right)\left(x^2+4x+3\right)\)

a) Ta có: \(x^3+4x-5\)

\(=x^3-x+5x-5\)

\(=x\left(x-1\right)\left(x+1\right)+5\left(x-1\right)\)

\(=\left(x-1\right)\left(x^2+x+5\right)\)

b) Ta có: \(x^3-3x^2+4\)

\(=x^3+x^2-4x^2+4\)

\(=x^2\left(x+1\right)-4\left(x-1\right)\left(x+1\right)\)

\(=\left(x+1\right)\left(x^2-4x+4\right)\)

\(=\left(x+1\right)\cdot\left(x-2\right)^2\)

c) Ta có: \(x^3+2x^2+3x+2\)

\(=x^3+x^2+x^2+x+2x+2\)

\(=x^2\left(x+1\right)+x\left(x+1\right)+2\left(x+1\right)\)

\(=\left(x+1\right)\left(x^2+x+2\right)\)

d) Ta có: \(x^2+2xy+y^2+2x+2y-3\)

\(=\left(x+y\right)^2+2\left(x+y\right)-3\)

\(=\left(x+y\right)^2+3\left(x+y\right)-\left(x+y\right)-3\)

\(=\left(x+y\right)\left(x+y+3\right)-\left(x+y+3\right)\)

\(=\left(x+y+3\right)\left(x+y-1\right)\)

e) Ta có: \(\left(x^2+3x\right)^2-2\left(x^2+3x\right)-8\)

\(=\left(x^2+3x\right)^2-4\left(x^2+3x\right)+2\left(x^2+3x\right)-8\)

\(=\left(x^2+3x\right)\left(x^2+3x-4\right)+2\left(x^2+3x-4\right)\)

\(=\left(x^2+3x-4\right)\left(x^2+3x+2\right)\)

\(=\left(x+4\right)\left(x-1\right)\left(x+1\right)\left(x+2\right)\)

f) Ta có: \(\left(x^2+4x+10\right)^2-7\left(x^2+4x+11\right)+7\)

\(=\left(x^2+4x+10\right)^2-7\left(x^2+4x+10\right)-7+7\)

\(=\left(x^2+4x+10\right)\left(x^2+4x+10-7\right)\)

\(=\left(x^2+4x+3\right)\left(x^2+4x+10\right)\)

\(=\left(x+1\right)\left(x+3\right)\left(x^2+4x+10\right)\)

b) 4x² - 3x - 1

vì 4x² lớn hơn hoặc bằng 0

=> 4x² - 3x - 1 lớn hơn hoặc bằng 1 > 0

=> đa thức này ko có nghiệm 

t i c k mk nhoa oa oa buồn ngủ rùi ^ 0 ^ !!!!