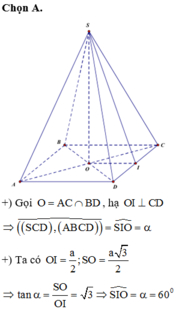
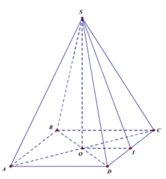
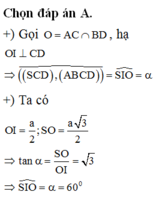cho hình chóp tứ giác đều có cạnh đáy bằng a; đoòng cao h. tìm mối liên hệ giữa a và h để tỉ số thể tích khối cầu nội tiếp và ngoại tiếp hình chóp đạt giá trị lớn nhất
DH
Những câu hỏi liên quan
Cho hình chóp tứ giác đều có cạnh đáy bằng a và cạnh bên bằng
a
6
2
. Thể tích khối chóp đã cho là A.
a
3
B.
2
a
3
3
C.
a
3
3
D.
4...
Đọc tiếp
Cho hình chóp tứ giác đều có cạnh đáy bằng a và cạnh bên bằng a 6 2 . Thể tích khối chóp đã cho là
A. a 3
B. 2 a 3 3
C. a 3 3
D. 4 a 3 3
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 600. Tính thể tích khối chóp S.ABCD. A.
a
3
6
B.
a
3
6
3
C.
a
3...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 600. Tính thể tích khối chóp S.ABCD.
A. a 3 6
B. a 3 6 3
C. a 3 6 6
D. a 3 6 2
Đáp án C
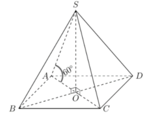
Gọi O là tâm đáy ABCD. Khi đó S O ⊥ A B C D
suy ra AO là hình chiếu vuông góc của SA lên mặt phẳng đáy. Khi đó góc giữa cạnh bên SA và đáy là S A O ^
Suy ra S A O ^ = 60 °
Vậy thể tích khối chóp là:
V = 1 3 . S O . S A B C D = a 3 6 6
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với đáy một góc
30
°
.Thể tích V của khối chóp S.ABCD bằng A.
V
a
3
6
9
.
B.
V
a
3
6
18
.
C. ...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với đáy một góc 30 ° .Thể tích V của khối chóp S.ABCD bằng
A. V = a 3 6 9 .
B. V = a 3 6 18 .
C. V = a 3 3 9 .
D. V = a 3 3 6 .
Đáp án B.
Chiều cao khối chóp:
h = a 2 2 . tan 30 ° = a 6 6 .
Do đó
V = 1 3 a 2 . h = 1 3 a 2 . a 6 6 = 6 a 3 18 .
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng
60
0
. Tính thể tích khối chóp S.ABCD. A.
a
3
6
2
B.
a
3
6
6
C. ...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60 0 . Tính thể tích khối chóp S.ABCD.
A. a 3 6 2
B. a 3 6 6
C. a 3 6
D. a 3 6 3
Đáp án B
Ta có: 2 B I 2 = a 2 ⇒ B I = a 2 ; S I = B I tan 60 0 = a 3 2
Thể tích khối chóp S.ABCD là
V = 1 3 S I . S A B C D = 1 3 a 3 2 . a 2 = a 3 6 6
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng
60
0
. Tính thể tích khối chóp S.ABCD A.
a
3
6
2
B.
a
3
6
6
C. ...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60 0 . Tính thể tích khối chóp S.ABCD
A. a 3 6 2
B. a 3 6 6
C. a 3 6
D. a 3 6 3
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, chiều cao của chóp bằng
a
3
2
. Góc giữa mặt bên và mặt đáy bằng A.
60
°
B.
75
°
C.
30
°
D.
45
°
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, chiều cao của chóp bằng a 3 2 . Góc giữa mặt bên và mặt đáy bằng
A. 60 °
B. 75 °
C. 30 °
D. 45 °
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, chiều cao của chóp bằng
a
3
2
. Góc giữa mặt bên và mặt đáy bằng
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, chiều cao của chóp bằng a 3 2 . Góc giữa mặt bên và mặt đáy bằng
![]()
![]()
![]()
![]()
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, đường cao của hình chóp bằng
a
3
2
. Tính số đo góc giữa mặt bên và đáy A.
30
o
B.
45
o
C.
60
o
D.
90
o
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, đường cao của hình chóp bằng a 3 2 . Tính số đo góc giữa mặt bên và đáy
A. 30 o
B. 45 o
C. 60 o
D. 90 o
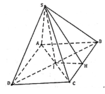
Ta có:
S I = a 3 2 ; I H = a 2 ⇒ tan I H S ^ = S I H I = 3 ⇒ S B C ; A B C D ^ = I H S ^ = 60 o
Đáp án C
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều có cạnh đáy bằng 10m và chiều cao của mặt bên xuất phát từ đỉnh của hình chóp tứ giác đều bằng 12m.Diện tích toàn phần của hình chóp này là
Sxq=1/2*10*4*12=2*10*12=2*120=240cm2
Stp=240+10^2=340cm2
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a cạnh bên hợp với mặt đáy một góc 600. Tính theo a thể tích khối chóp S.ABCD. A.
V
6
a
3
6
B.
V
6...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a cạnh bên hợp với mặt đáy một góc 600. Tính theo a thể tích khối chóp S.ABCD.
A. V = 6 a 3 6
B. V = 6 a 3 2
C. V = 6 a 3 3
D. V = a 3 3
Chọn A.
Gọi H là tâm của hình vuông ABCD thì SH ⊥ (ABCD)
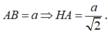
Do đó
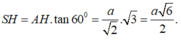
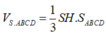
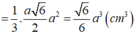
Đúng 0
Bình luận (0)