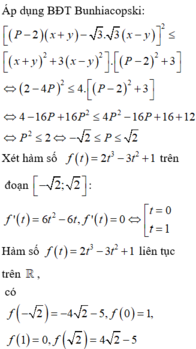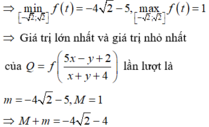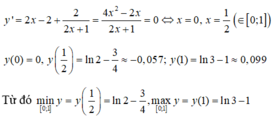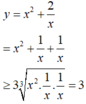Tìm giá trị nhỏ nhất của A =(x2-2x+2007)/x2 và giá trị của x>0 tương ứng
HP
Những câu hỏi liên quan
cho X, y>=0 sao cho X2+ Y2=1. Tìm giá trị nhỏ nhất và giá trị lớn nhất của A= √2X+1+√2Y+1
với x;y>=0 ta có:
\(A^2=\left(\sqrt{2x+1}+\sqrt{2y+1}\right)^2=2x+1+2y+1+2\sqrt{\left(2x+1\right)\left(2y+1\right)}\)
\(=2\left(x+y\right)+2+\sqrt{4xy+2x+2y+1}=2\left(x+y\right)+2+\sqrt{4xy+2\left(x+y\right)+1}\)
\(2=2\left(x^2+y^2\right)=\left(1+1\right)\left(x^2+y^2\right)>=\left(x+y\right)^2\Rightarrow x+y< =\sqrt{2}\)(bđt bunhiacopxki)
\(2xy< =x^2+y^2=1\Rightarrow2\cdot2xy=4xy< =2\cdot1=2\)
\(\Rightarrow A^2=2\left(x+y\right)+2+2\sqrt{4xy+2\left(x+y\right)+1}< =2\sqrt{2}+2+2\sqrt{2+2\sqrt{2}+1}\)
\(=2\sqrt{2}+2+2\sqrt{\left(\sqrt{2}+1\right)^2}=2\sqrt{2}+2+2\left(\sqrt{2}+1\right)4\sqrt{2}+4\)
\(\Rightarrow A< =\sqrt{4\sqrt{2}+4}\)
dấu = xảy ra khi x=y=\(\sqrt{\frac{1}{2}}\)
vậy max A là \(\sqrt{4\sqrt{2}+4}\)khi \(x=y=\sqrt{\frac{1}{2}}\)
Đúng 0
Bình luận (0)
Cho biểu thức : A= x-1/3x và B= ( x+1/2x-2 + 3x-1/x2 - 1 - x+3/2x+2) : 3/x+1 Với x # 0,x# -1,1.
a)Rút gọn biểu thức B
b)Tính giá trị của biểu thức A khi x thỏa mãn x2 - 2x = 0
c) tìm giá trị của x để B/A đạt giá trị nhỏ nhất .
b: \(A=\dfrac{2-1}{3\cdot2}=\dfrac{1}{6}\)
Đúng 0
Bình luận (0)
Cho x và y là đại lượng tỉ lệ thuận .
y1 ; y2 là các giá trị của y tương ứng với x1;x2 của x
a, Tìm các giá trị của y tương ứng với x = x1+x2.
b, Tìm các giá trị của y tương ứng với x = -2/7.x1
c, Tìm các giá trị của y tương ứng với x = x1/x2.
Giúp mink với nha các bạn !!!!!!!!
Cho pt : x^2-(m+1)x+m=0.
Gọi x1, x2 là hai nghiệm của pt. Tìm giá trị m để A=x1^2x2+x1x2^2+2007 đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
Mọi người giúp giùm... cảm ơn ạk
Cho x và y là đại lượng tỉ lệ thuận .
y1; y2 là các giá trị của y tương ứng với x1 ; x2 của x
a, Tìm các giá trị của y tương ứng với x = x1 + x2 .
b, Tìm các giá trị của y tương ứng với x =-2/7 . x1
c, Tìm các giá trị của y tương ứng với x = x1/x2 .
Giúp mink với nha các bạn !
Cho các số thực x, y thay đổi thỏa mãn
x
2
+
y
2
-
x
y
1
và hàm số
f
t
2
t
3
-
3
t
2
-
1
. Gọi M, m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của
Q
f...
Đọc tiếp
Cho các số thực x, y thay đổi thỏa mãn x 2 + y 2 - x y = 1 và hàm số f t = 2 t 3 - 3 t 2 - 1 . Gọi M, m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của Q = f 5 x - y + 2 x + y + 4 . Tổng M + m bằng
A. - 4 - 3 2
B. - 4 - 5 2
C. - 4 - 4 2
D. - 4 - 2 2
Tìm giá trị của m để phương trình
x
2
+ (4m + 1)x + 2(m – 4) 0 có hai nghiệm
x
1
;
x
2
và biểu thức
A
(
x
1
−
x
2
)
2
đạt giá trị nhỏ nhất A. m 1 B. m 0...
Đọc tiếp
Tìm giá trị của m để phương trình x 2 + (4m + 1)x + 2(m – 4) = 0 có hai nghiệm x 1 ; x 2 và biểu thức A = ( x 1 − x 2 ) 2 đạt giá trị nhỏ nhất
A. m = 1
B. m = 0
C. m = 2
D. m = 3
Phương trình x 2 + (4m + 1)x + 2(m – 4) = 0 có a = 1 ≠ 0 và
∆ = ( 4 m + 1 ) 2 – 8 ( m – 4 ) = 16 m 2 + 33 > 0 ; ∀ m
Nên phương trình luôn có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có x 1 + x 2 = − 4 m − 1 x 1 . x 2 = 2 n − 8
Xét
A = x 1 - x 2 2 = x 1 + x 2 2 - 4 x 1 x 2 = 16 m 2 + 33 ≥ 33
Dấu “=” xảy ra khi m = 0
Vậy m = 0 là giá trị cần tìm
Đáp án: B
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
y
x
2
-
2
x
+
l
n
(
2
x
+
1
)
trên [0; 1] A.
m
a
x
0
;
1
y
ln
3
+
1
;
m...
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x 2 - 2 x + l n ( 2 x + 1 ) trên [0; 1]
A. m a x 0 ; 1 y = ln 3 + 1 ; m i n 0 ; 1 y = ln 2
B. m a x 0 ; 1 y = ln 3 - 1 ; m i n 0 ; 1 y = 0
C. m a x 0 ; 1 y = ln 3 - 1 ; m i n 0 ; 1 y = ln 2 - 3 4
D. m a x 0 ; 1 y = ln 2 + 3 4 ; m i n 0 ; 1 y = ln 3 - 1
Tìm giá trị nhỏ nhất m của hàm số
y
x
2
+
2
x
,
x
0
A. m 2 B. m 3 C. m 4 D. m 5
Đọc tiếp
Tìm giá trị nhỏ nhất m của hàm số y = x 2 + 2 x , x > 0
A. m = 2
B. m = 3
C. m = 4
D. m = 5
Tìm giá trị lớn nhất và nhỏ nhất của các hàm số sau trên các khoảng, đoạn tương ứng: f(x) = x 4 – 4 x 2 + 1 trên đoạn [-1; 2]
min f(x) = f( 2 ) = −3; max f(x) = f(2) = f(0) = 1
Đúng 0
Bình luận (0)