Cho góc nhọn α. Chứng minh rằng:
Sinα< tanα và cosα<cotα.
Cho α là góc nhọn, chứng minh rằng:
1 - tan α 1 + tan α = cos α - sin α cos α + sin α
a/ Không sử dụng máy tính .Cho góc nhọn α , biết sinα = \(\dfrac{\sqrt{3}}{2}\) . Hãy tính cosα ; tanα ; cotα.
b/ Không sử dụng máy tính .Cho góc nhọn α , biết cosα = \(\dfrac{\sqrt{5}}{7}\) . Hãy tính cosα ; tanα ; cotα.
a: \(\cos\alpha=\dfrac{1}{2}\)
\(\tan\alpha=\sqrt{3}\)
\(\cot\alpha=\dfrac{\sqrt{3}}{3}\)
Cho α là góc nhọn và cosα = 3/4
Hãy tìm sinα, tanα và cotgα
Vì α là góc nhọn nên ta có sinα > 0.
Ta lại có: sin 2 α + cos 2 α = 1
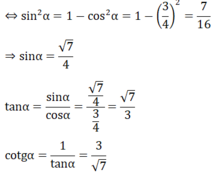
Cho α là góc nhọn, sinα = 1/2.Tính cosα;tanα;cotα
Cho α là góc nhọn, sinα = 1/2. Tính cosα; tanα; cotα
Ta có: sin 2 α + cos 2 α = 1
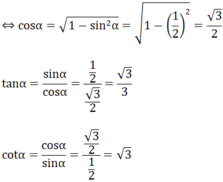
Cho góc nhọn α
Chứng minh rằng: 1 - t g α 1 + t g α = cos α - sin α cos α + sin α
Dựng góc nhọn α,biết:
a, sinα = 2 3
b, cosα = 2 5
c, tanα = 2
d, cotα = 4 5
Dựng góc nhọn α,biết:
a, sinα = 3 5
b, cosα = 4 7
c, tanα = 3 2
d, cotα = 5 6
Dựng một tam giác vuông ta có:
a, Độ dài cạnh góc vuông là 3, cạnh huyền là 5, góc đối diện với cạnh góc vuông đó là góc α
b, Độ dài cạnh góc vuông là 4, cạnh huyền là 7,góc giữa cạnh góc vuông và cạnh huyền đó là góc α
c, Độ dài hai cạnh góc vuông là 3 và 2, góc đối diện với cạnh góc vuông độ dài 3 là góc α
d, Độ dài hai cạnh góc vuông là 5 và 6, góc đối diện với cạnh góc vuông độ dài 6 là góc α
Cho A B C ^ = 60 0 và ∆ABC tam giác nhọn
a, Tính sinα, tanα, cotα, biết cosα = 1 5
b, Tính cosα, tanα, cotα, biết sinα = 2 3
c, Cho tanα = 2. Tính sinα, cosα, cotα
d, Cho cotα = 3. Tính sinα, cosα, tanα
a, Tìm được sinα = 24 5 , tanα = 24 , cotα = 1 24
b, cosα = 5 3 , tanα = 2 5 , cotα = 5 2
c, sinα = ± 2 5 , cosα = ± 1 5 , cotα = 1 2
d, sinα = ± 1 10 , cosα = ± 3 10 , tanα = 1 3
Cho góc α thỏa mãn tanα = 2 và 1800< α< 2700 . Tính P = cosα + sinα
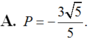
![]()

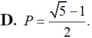
Cho ΔABC vuông tại A có góc B =α .Chứng minh rằng
a/ tanα=sinα trên cosα ;cotgα =cosα trên sinα;tanα.cotgα =1
b/ sin2α +cos2 α =1
Giúp mình bài này nha .mình cám ơn![]()
Xét tam giác vuông có ba cạnh AB, AC , BC lần lượt là c,b,a
a) Ta có : \(tan\alpha=\frac{b}{c}=\frac{\frac{b}{a}}{\frac{c}{a}}=\frac{sin\alpha}{cos\alpha}\)
\(cotg\alpha=\frac{c}{b}=\frac{\frac{c}{a}}{\frac{b}{a}}=\frac{cos\alpha}{sin\alpha}\)
\(tan\alpha.cotg\alpha=\frac{b}{c}.\frac{c}{b}=1\)
b) Ta có : \(sin^2\alpha=\frac{b^2}{a^2},cos^2\alpha=\frac{c^2}{a^2}\Rightarrow sin^2\alpha+cos^2\alpha=\frac{b^2+c^2}{a^2}=\frac{a^2}{a^2}=1\)