Cho tam giác ABC có AB=AC.Trên cạnh BC lấy D,E sao cho BD=CE,BD<BE.CM AD=AE.
Help me!
DL
Những câu hỏi liên quan
cho tam giác ABC có AB = AC.Trên cạnh AB lấy điểm E,trên cạnh AC lấy điểm D sao cho AE=AD.Gọi I là giao điểm của BD và CE, F là trung điểm của BC.
CMR: a,BD = CE
b,TAM GIÁC CEB= TAM GIÁC BDC
c, TAM GIÁC BIE = TAM GIÁC CID
d, A,I,F thẳng hàng
Cho tam giác ABC có AB=AC.TRên cạnh AB lấy điểm E,trên cạnh AC lấy điểm D sao cho AE=AD. Gọi F là giao điểm của BD và CE, H là trung điểm của BC. Chứng minh rằng :
a)tam giác ADB = Tam giác AEC
b)BF=CF
c)Ba điểm A,F,H thẳng hàng
Cho tam giác ABC có AB=AC.Trên cạnh BC lấy D,E sao cho BD=DE=EC .CMR trong 3 góc :BAD;DAE:EAC thi góc DAE lớn nhất
Cho tam giác ABC có AB<AC.Trên AC lấy D sao cho AD=AB.Gọi M là trung điểm BD.
a)Tam giác ABM=tam giác ADM
b)CM AM vuông góc BD
c)Tia AM cắt cạnh BC tại K. CM tam giác ABK= tam giác ADK
d)Trên tia đối tia BA lấy F sao cho BF=OC. CM F, K,D thẳng hàng
e) CM BC=DF
f) BD//FC
cho hình tam giác abc có diện tích 120cm vuông.D là trung điểm của cạnh AC.Trên cạnh AB lấy điểm E sao cho BE= một phần ba BA.Nối B với D và nối C với E.Hai đoạn thẳng BD và CE cắt nhau tại G.Tính diện tích hình tam giác GBC
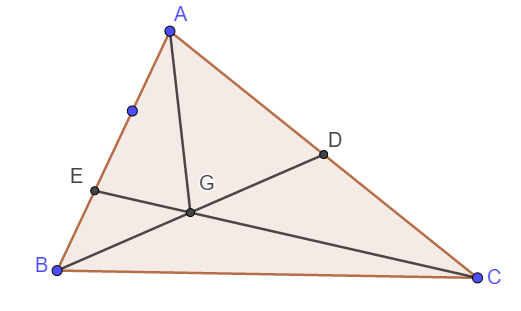
Ta thấy AE = 2BE nên ta có chiều cao hạ từ A xuống EC bằng 2 lần chiều cao hạ từ B xuống EC.
Từ đó ta có:
\(S_{AGC}=2S_{BGC}\) (Chung cạnh đáy GC)
Lại có tam giác AGD và tam giác GCD có cạnh đáy AD bằng cạnh đáy DC và chung chiều cao hạ từ G xuống AC nên \(S_{AGD}=S_{GCD}\Rightarrow S_{GDC}=\frac{1}{2}S_{AGC}\Rightarrow S_{GDC}=S_{GBC}=\frac{1}{2}S_{BDC}\)
Ta có \(S_{BDC}=\frac{1}{2}S_{ABC}=\frac{1}{2}.120=60\left(cm^2\right)\)
\(\Rightarrow S_{GBC}=60:2=30\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = AC, lấy điểm E trên cạnh AB, lấy điểm D trên cạnh AC sao cho AE = AD; BD và CE cắt nhau tại M.
a) Chứng minh: BD = CE
b) Chứng minh: tam giác BEM = tam giác CDM
c) Chứng minh: AM vuonong góc với BC
d) Chứng minh: ED // BC
xét \(\Delta\) ABD và \(\Delta\)ACE có góc A chung; AB= AC(gt); AE= AD, suy ra : \(\Delta\)ABD = \(\Delta\)ACE( c.g.c) => BD = CE
Đúng 0
Bình luận (0)
cho tam giác abc vuông tại a có ab>ac, trên cạnh AB lấy D sao cho BD = AC.Trên cạnh AC lấy E sao cho CE=AD, gọi O là giao điểm của CD và BE.Trên đường vuông góc với AB vẽ tại B lấy F sao cho BF=CE(F,C cùng thuộc một nửa mặt phẳng bờ AB).chứng minh
a)DF=DC
b)Tam giác CDF vuông cân từ đó tính số đó COE
TÍNH ^COE kiểu j thế bn
Cho tam giác ABC cân tại A, lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho BD=CE. Chứng minh DE//BC
Ta có: \(AB=AC.BD=CE\) ⇒ \(AD=AE\)
⇒ △ ADE cân tại A
⇒ \(\widehat{ADE}=\dfrac{180-A}{2}\) \(\left(1\right)\)
Ta có: △ ABC cân tại A
⇒ \(\widehat{B}=\dfrac{180-A}{2}\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) suy ra: \(\widehat{B}=\widehat{D}\)
Mà ta thấy 2 góc này ở vị trí đồng vị nên suy ra DE // BC
Đúng 0
Bình luận (0)
Xét ΔABC có
\(\dfrac{BD}{AB}=\dfrac{CE}{AC}\)
nên DE//BC
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB=5cm,AC=7cm,BC=9cm.Trên tia AB lấy D sao cho BD=BA.Trên tia AC lấy E sao cho CE=CA.Kéo dài trung điểm AM thuộc tam giác ABC: MI=MA
a) tính độ dài các cạnh của tam giác ADE
b) tính DI//BC
c)C/m D;I;E thẳng hàng
Cho tam giác ABC cân đỉnh A. Trên cạnh AB lấy điểm D, trên tia đối của CA lấy điểm E sao cho BD = CE. Nối D với E. Cmr: BC<CE