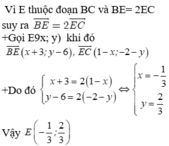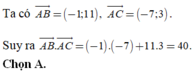trong mặt phẳng tọa độ oxy cho ba điểm a(-1;2),b(3;0),c(3;5) tính các cạnh của tam giác abc. suy ra tam giác abc là tam giác cân
DL
Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy, cho hai điểm M (-2; 2) và N (1; 1). Tìm tọa độ điểm P thuộc trục hoành sao cho ba điểm M, N, P thẳng hàng.
A. P( 2; 0 )
B. P( 3; 0)
C. P(- 4; 0)
D. P(4;0)
Ta có P ∈ O x nên P( x; 0) và M P → = x + 2 ; − 2 M N → = 3 ; − 1 .
Do M, N, P thẳng hàng nên 2 vecto M P → ; M N → cùng phương
⇒ x + 2 3 = − 2 − 1 = 2 ⇔ x + 2 = 6 ⇔ x = 4 ⇒ P 4 ; 0 .
Chọn D.
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(-2; 2) và N(1; 1).Tìm tọa độ điểm P thuộc trục hoành sao cho ba điểm M; N; P thẳng hàng.
A. P(0; 4)
B. P(0; -4)
C. P(-4; 0)
D.P( 4; 0)
Ta có P ∈ O x nên P(x; 0) và M P → = x + 2 ; − 2 M N → = 3 ; − 1 .
Do M, N, P thẳng hàng nên x + 2 3 = − 2 − 1 ⇔ x = 4 ⇒ P 4 ; 0 .
Chọn D.
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A (-4; 1), B (2;4), C (2; -2)
a) Giải tam giác
b) Tìm tọa độ trực tâm H của tam giác ABC.
a) Ta có:
\(\left\{ \begin{array}{l}\overrightarrow {AB} = (2 - ( - 4);4 - 1) = (6;3)\\\overrightarrow {BC} = (2 - 2; - 2 - 4) = (0; - 6)\\\overrightarrow {AC} = (2 - ( - 4); - 2 - 1) = (6; - 3)\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{6^2} + {3^2}} = 3\sqrt 5 \\BC = \left| {\overrightarrow {BC} } \right| = \sqrt {{0^2} + {{( - 6)}^2}} = 6\\AC = \left| {\overrightarrow {CA} } \right| = \sqrt {{6^2} + {{( - 3)}^2}} = 3\sqrt 5 .\end{array} \right.\)
Áp dụng định lí cosin cho tam giác ABC, ta có:
\(\cos \widehat A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{{\left( {3\sqrt 5 } \right)}^2} + {{\left( {3\sqrt 5 } \right)}^2} - {{\left( 6 \right)}^2}}}{{2.3\sqrt 5 .3\sqrt 5 }} = \frac{3}{5}\)\( \Rightarrow \widehat A \approx 53,{13^o}\)
\(\cos \widehat B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}} = \frac{{{{\left( 6 \right)}^2} + {{\left( {3\sqrt 5 } \right)}^2} - {{\left( {3\sqrt 5 } \right)}^2}}}{{2.6.3\sqrt 5 }} = \frac{{\sqrt 5 }}{5}\)\( \Rightarrow \widehat B \approx 63,{435^o}\)
\( \Rightarrow \widehat C \approx 63,{435^o}\)
Vậy tam giác ABC có: \(a = 6;b = 3\sqrt 5 ;c = 3\sqrt 5 \); \(\widehat A \approx 53,{13^o};\widehat B = \widehat C \approx 63,{435^o}.\)
b)
Gọi H có tọa độ (x; y)
\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AH} = (x - ( - 4);y - 1) = (x + 4;y - 1)\\\overrightarrow {BH} = (x - 2;y - 4)\end{array} \right.\)
Lại có: H là trực tâm tam giác ABC
\( \Rightarrow AH \bot BC\) và \(BH \bot AC\)
\( \Rightarrow \left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = {90^o} \Leftrightarrow \cos \left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = 0\) và \(\left( {\overrightarrow {BH} ,\overrightarrow {AC} } \right) = {90^o} \Leftrightarrow \cos \left( {\overrightarrow {BH} ,\overrightarrow {AC} } \right) = 0\)
Do đó \(\overrightarrow {AH} .\overrightarrow {BC} = \overrightarrow 0 \) và \(\overrightarrow {BH} .\overrightarrow {AC} = \overrightarrow 0 \).
Mà: \(\overrightarrow {BC} = (0; - 6)\)
\( \Rightarrow (x + 4).0 + (y - 1).( - 6) = 0 \Leftrightarrow - 6.(y - 1) = 0 \Leftrightarrow y = 1.\)
Và \(\overrightarrow {AC} = (6; - 3)\)
\(\begin{array}{l} \Rightarrow (x - 2).6 + (y - 4).( - 3) = 0\\ \Leftrightarrow 6x - 12 + ( - 3).( - 3) = 0\\ \Leftrightarrow 6x - 3 = 0\\ \Leftrightarrow x = \frac{1}{2}.\end{array}\)
Vậy H có tọa độ \(\left( {\frac{1}{2}}; 1 \right)\)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(3;-1); B(2; 10); C(-4; 2). Tính tích vô hướng
A
B
→
.
A
C
→
.
A.
A
B
→
.
A
C
→
40.
B.
A
B...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(3;-1); B(2; 10); C(-4; 2). Tính tích vô hướng A B → . A C → .
A. A B → . A C → = 40.
B. A B → . A C → = − 40.
C. A B → . A C → = 26.
D. A B → . A C → = - 26.
Ta có A B → = − 1 ; 11 , A C → = − 7 ; 3 .
Suy ra A B → . A C → = − 1 . − 7 + 11.3 = 40.
Chọn A.
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(3; -1); B(2; 10); C(-4; 2). Tính tích vô hướng A B → . A C → .
A. 40
B. – 40
C. 26
D. – 26
Ta có A B → = − 1 ; 11 , A C → = − 7 ; 3 .
Suy ra A B → . A C → = − 1 . − 7 + 11.3 = 40.
Chọn A.
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(6,3) ; B(-3;6) và C(1; -2). Xác định điểm E trên cạnh BC sao cho BE 2EC. A.
E
-
1
3
;
2
3
B.
E
-
1
3
;
-...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(6,3) ; B(-3;6) và C(1; -2). Xác định điểm E trên cạnh BC sao cho BE= 2EC.
A. E - 1 3 ; 2 3
B. E - 1 3 ; - 2 3
C. E 2 3 ; - 1 3
D. E - 2 3 ; 1 3
Trong mặt phẳng tọa độ Oxy cho ba điểm A( 2; -1) ; B( 2; 10) và C(-4; 2). Tính tích vô hướng A B → . A C →
A. 33
B. 17
C. 24
D. 33
Trong mặt phẳng tọa độ Oxy, cho ba điểm
A
3
;
−
1
,
B
2
;
10
,
C
−
4
;
2
.
Tính tích vô hướng
A
B
→
.
A
C
→
.
A. 40...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho ba điểm A 3 ; − 1 , B 2 ; 10 , C − 4 ; 2 . Tính tích vô hướng A B → . A C → .
A. 40
B. – 40
C. 26
D. – 26
Trong mặt phẳng Oxy, cho ba điểm A, B, C với B là trung điểm của đoạn thẳng AC. Tìm tọa độ điểm C, biết A(1; 3) và B(2; -1).
\(\left\{{}\begin{matrix}x_B=\dfrac{x_A+x_C}{2}\\y_B=\dfrac{y_A+y_C}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}1+x_C=4\\3+y_C=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_C=3\\y_C=-5\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho ba điểm A(1;1;1), B(-1;-1;0), C(3;1;-1). Tìm tọa độ điểm N trên mặt phẳng (Oxy) cách đều ba điểm A, B, C. A.
N
2
;
-
4
7
;
0
B. N(2;0;0) C.
N
2
;
7
4...
Đọc tiếp
Cho ba điểm A(1;1;1), B(-1;-1;0), C(3;1;-1). Tìm tọa độ điểm N trên mặt phẳng (Oxy) cách đều ba điểm A, B, C.
A. N 2 ; - 4 7 ; 0
B. N(2;0;0)
C. N 2 ; 7 4 ; 0
D. N(0;0;2)
Chọn A
Điểm N(x;y;0). Tìm x;y từ hệ hai phương trình NA = NB = NC.
Đúng 0
Bình luận (0)