tính góc C biết sinC=3/5
TV
Những câu hỏi liên quan
Cho tam giác abc vuông tại a biết sinC=\(\frac{3}{5}\). Hãy tính tỉ số lượng giác của C.Từ đó suy ra tỉ số lượng giác góc B.
\(\cos C=\sqrt{1-\sin^2C}=\sqrt{1-\frac{9}{25}}=\sqrt{\frac{16}{25}}\)
\(\Rightarrow\cos C=\frac{4}{5}\)
\(\Rightarrow\tan C=\frac{\sin C}{\cos C}=\frac{3}{5}:\frac{4}{5}=\frac{3}{4}\)và \(\cot C=\frac{4}{3}\)
Ta có: \(\widehat{C};\widehat{B}\)là hai góc phụ nhau
\(\Rightarrow\hept{\begin{cases}\sin C=\cos B\\\cos C=\sin B\end{cases};\hept{\begin{cases}\tan C=\cot B\\\cot C=\tan B\end{cases}}}\)
\(\Rightarrow\sin B=\frac{4}{5};\cos B=\frac{3}{5};\tan B=\frac{4}{3};\cot B=\frac{3}{4}\)
Ta có: \(\sin C=\frac{AB}{BC}=\frac{3}{5}\)
=> \(\frac{AB}{3}=\frac{BC}{5}=k\left(k\inℕ\right)\)
=> \(\hept{\begin{cases}AB=3k\\BC=5k\end{cases}}\)
=> \(AC=\sqrt{\left(5k\right)^2-\left(3k\right)^2}=\sqrt{16k^2}=4k\)
Đến đây thì xong rồi:))
\(\sin B=\frac{AC}{BC}=\frac{4k}{5k}=\frac{4}{5}\) ; \(\cos B=\frac{AB}{BC}=\frac{3k}{5k}=\frac{3}{5}\)
\(\tan B=\frac{AC}{AB}=\frac{4k}{3k}=\frac{4}{3}\) ; \(\cot B=\frac{AB}{AC}=\frac{3k}{4k}=\frac{3}{4}\)
cho tam giác ABC , góc A = 90 độ , biết sinC = 1/2 . Tính các tỉ số lượng giác của góc B
cho tam giác ABC vuông tại A. Biết tanC= 0.75. Không tính số đo góc, tính cotC, sinC, cosC
cotC=1/tanC = 4/3
=>\(\frac{ac}{ab}=\frac{4}{3}\)=>ac=4k , ab=3k {với k \(\ge\) 0 }
=>BC = 5k
=>sinC =\(\frac{3}{5}\)
cosC=\(\frac{4}{5}\)
tick nha
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A Biết :
1. sinc=1/3 tính AC. 2. cosc=2/5 tính AC
mong mn giúp đỡ
Câu 6: Cho tam giác ABC vuông tại A, biết sinC = 0,6. Tính các tỉ số lượng giác của góc B
\(\cos\widehat{B}=0.6\)
\(\sin\widehat{B}=0.8\)
\(\tan\widehat{B}=\dfrac{4}{3}\)
\(\cot\widehat{B}=\dfrac{3}{4}\)
Đúng 0
Bình luận (0)
a)Cho tam giác ABC vuông tại A, biết AB=4cm; BC=5cm, Tonhs cosC+TanB
b) Cho tam giác ABC vuông tại A, có AB=5cm,BC=10cm. Tính sinC và số đo góc B
c) Cho tam giác ABC vuông tại A, biết cosB=8cm. hãy tính các tỉ số lượng giác của góc C. E c.ơn ạ!
Câu a) với b) tính cos, tan, sin là tính góc hay cạnh vậy cậu?
Đúng 0
Bình luận (9)
a) Xét \(\Delta ABC\) vuông tại `A`
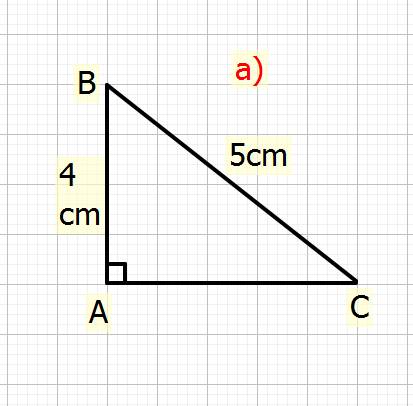
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)
\(\Rightarrow5^2=4^2+AC^2\\ \Rightarrow AC^2=5^2-4^2\\ \Rightarrow AC^2=25-16=9\\ \Rightarrow AC=\sqrt{9}=3cm\)
Vậy: \(AC=3cm\)
Ta có: \(CosC=\dfrac{AC}{BC}\left(tslg\right)\)
\(\Rightarrow CosC=\dfrac{3}{5}\\ \Rightarrow CosC\approx53^o\)
Vậy: Góc C khoảng \(53^o\)
Ta có: \(TanB=\dfrac{AC}{AB}\left(tslg\right)\)
\(\Rightarrow TanB=\dfrac{3}{4}\\ \Rightarrow TanB\approx37^o\)
Vậy: Góc B khoảng \(37^o\)
_
b) Xét \(\Delta ABC\) vuông tại `A`
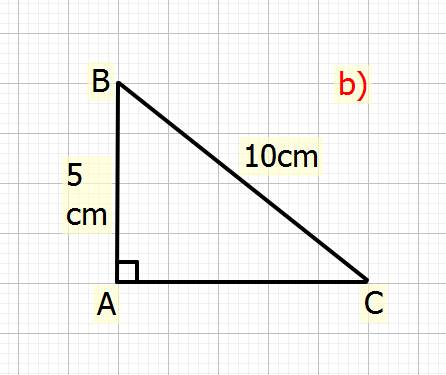
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)
\(\Rightarrow10^2=5^2+AC^2\\ \Rightarrow AC^2=10^2-5^2\\\Rightarrow AC^2=100-25=75\\ \Rightarrow AC=\sqrt{75}=5\sqrt{3}cm\)
Vậy: \(AC=5\sqrt{3}cm\)
Ta có: \(SinC=\dfrac{AB}{BC}\left(tslg\right)\)
\(\Rightarrow SinC=\dfrac{5}{10}\\ \Rightarrow30^o\)
Vậy: Góc C là \(30^o\)
Ta có: \(SinB=\dfrac{AC}{BC}\left(tslg\right)\)
\(\Rightarrow SinB=\dfrac{5\sqrt{3}}{10}\\ \Rightarrow SinB=60^o\)
Vậy: Góc B là \(60^o\).
Đúng 1
Bình luận (2)
Cho tam giác ABC vuông tại A, có AH là đường cao.1. Biết AH 2/6 cm, BH 4 cm.a) Tính độ dài các đoạn thẳng HC, ACb) Tính số đo góc ABH (làm tròn đến độ)2. Cho AC 3 .AB. Chứng minh: 3.tan C-cotC+ /sinC sin 45°3. Lấy điểm M trên đường tròn tâm B bán kính BA (M thuộc nửa mặt phẳng bờ BC, không chứa điểm A). Gọi SBMH là diện tích tam giác BMH, Sạc là diện tích tam giác BCM. Chứng minh rằng: SaMH SHCM .sinº ACB
Đọc tiếp
Cho tam giác ABC vuông tại A, có AH là đường cao.
1. Biết AH= 2/6 cm, BH = 4 cm.
a) Tính độ dài các đoạn thẳng HC, AC
b) Tính số đo góc ABH (làm tròn đến độ)
2. Cho AC = 3 .AB. Chứng minh: 3.tan C-cotC+ /sinC = sin 45°
3. Lấy điểm M trên đường tròn tâm B bán kính BA (M thuộc nửa mặt phẳng bờ BC, không chứa điểm A). Gọi SBMH là diện tích tam giác BMH, Sạc là diện tích tam giác BCM. Chứng minh rằng: SaMH =SHCM .sinº ACB
Cho tam giác ABC vuông tại A, đường cao AH. Tính sinB, sinC, biết:
a, AB = 13, BH = 5
b, BH = 3, CH = 4
a) Áp dụng đlí Py - ta - go cho tam giác HAB ( ^H =90^o )
Ta có : \(AB^2=AH^2+BH^2\)
\(13^2=AH^2+5^2\)
\(AH^2=13^2-5^2\)
\(\Rightarrow AH=\sqrt{13^2-5^2}\)
\(\sin B=\frac{AH}{AB}=\frac{\sqrt{13^2-5^2}}{13}\approx0,923\)
Áp dụng hệ thức lượng cho tam giác ABC( ^A = 90^o ) , đường cao AH , ta có :
\(AH^2=BH.HC\Rightarrow HC=\frac{AH^2}{BH}=\frac{12^2}{5}=28,8\)
=> BC = 5 + 28,8 = 33,8
\(\sin C=\frac{AB}{BC}=\frac{13}{33,8}\approx0,384\)
Vậy : \(\sin B\approx0,923\)
\(\sin C\approx0,384\)
Cho tam giác ABC vuông tại A, đường cao AH. Tính sinB;sinC biết rằng;
a)AB = 13;BH = 5 b)BH = 3;HC = 4
a: AH=căn 13^2-5^2=12
Xét ΔAHB vuông tại H có
sin B=AH/AB=12/13=cos C
cos B=sin C=BH/AB=5/13
tan B=cot C=AH/BH=12/5
cot B=tan C=BH/AH=5/12
b: AH=căn 3*4=2*căn 3(cm)
BC=3+4=7(cm)
AB=căn 3*7=căn 21(cm)
AC=căn 4*7=2*căn 7(cm)
Xét ΔABC vuông tại A có
sin B=cos C=AC/BC=2*căn 7/7
cos B=sin C=AB/BC=căn 21/7
tan B=cot C=2*căn 7/căn 21=2/căn 3
cot B=tan C=căn 21/2*căn 7=căn 3/2
Đúng 1
Bình luận (0)



