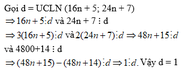\(\dfrac{16n+5}{24n+7}\) là phân số tối gản với n thuộc N
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
LA
Những câu hỏi liên quan
chứng tỏ rằng 16n+5/24n+7 là phân số tối giản với mọi n thuộc N
Đặt ƯCLN\(\left(16n+5;24n+7\right)=d\)
=> 16n + 5 chia hết cho d và 24n + 7 chia hết cho d.
=> 3.(16n + 5) - 2.(24n + 7) chia hết cho d.
=> 48n + 15 - 38n + 14 chia hết cho d
=> 1 chia hết cho d
=> d = 1
suy ra điều phải chứng tỏ
Đúng 0
Bình luận (0)
Gọi d là UCLN(16n+5;24n+7)
=>16n+5 chia hết cho d và 24n+7 chia hết cho d
Vì:16n+5 chia hết cho d=>48n+15 chia hết cho d
24n+7 chia hết cho d=>48n+14 chia hết cho d
Ta có:(48n+15)-(48n+14) chia hết cho d
= 1 chia hết cho d
Vì d=1 nên \(\frac{18n+5}{24n+7}\)là phân số tối giản với mọi n.
Mình làm bài này rồi,đề thi HSG lớp 6 có bài này.
Đúng 0
Bình luận (0)
a) Cho n thuộc N.Chứng minh A=14n+3/21n+5 là phân số tối giản
b) Cho n thuộc N. Chứng minh B=16n+5/24n+7 là phân số tối giản
a,Gọi d=(14n+3;21n+5)
=>14n+3 (2) và 21n+5 chia hết cho d
=>70n+15 và 63n+15 chi hết cho d => 7n chia hết cho d => 14n chia hết cho d (1)
Từ (1) và (2) => 3 chia hết cho d => d= 3 hoặc 1
+, Nếu d=3 => 21n+5 chia hết cho 3 => 5 chia hết cho 3 (vô lý) => d=1 =>đpcm
b, Gọi d=(16n+5;24n+7)
=> 16n+5 (4) và 24n+7 chia hết cho d
=>8n+2 chia hết cho d =>16n+4 chia hết cho d (3)
Từ (3) và (4) => d=1
Đúng 0
Bình luận (0)
chứng tỏ rằng phân số \(\frac{16n+5}{24n+7}\) là phân số tối giản với mọi n thuộc N
nhanh nha đầy đủ nuk mk tik liền
Đặt ƯCLN \(\left(16n+5;24n+7\right)\)
\(\Rightarrow\) 16 + 5 chia hết cho d và 24n + 7 chia hết cho d
\(\Rightarrow\) 3. ( 16n + 5 ) - 2 . ( 24n + 7 ) chia hết cho d
=> 48n + 15 - 38n + 14 chia hết cho d
=> 1 chia hết cho d
=> d = 1
Suy ra điều phải chứng tỏ
Đúng 0
Bình luận (0)
Đặt \(ưcln\)\(\left(16n-5:24n+7\right)\)=\(d\)
=> 16n + 5 chia hết cho d và 24n + 7 chia hết cho d.
=> 3.(16n + 5) - 2.(24n + 7) chia hết cho d.
=> 48n + 15 - 38n + 14 chia hết cho d
=> 1 chia hết cho d
=> d = 1
suy ra điều phải chứng tỏ
Đúng 0
Bình luận (0)
Nobita Kun tính sai rùi 48n-38n=10n chứ nhỉ ???
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a) tìm tất cả các phân số có tử bằng 15 lớn hơn 3/7 và nhỏ hơn 5/8
b) tính tổng S = 4/2.5 + 4/5.8 + 4/8.11 + ... 4/65.68
c) chứng tỏ rằng 16n + 5 / 24n + 7 là phân số tối giản với mọi n thuộc z
a) tìm tất cả các phân số có tử bằng 15 lớn hơn 3/7 và nhỏ hơn 5/8
b) tính tổng S = 4/2.5 + 4/5.8 + 4/8.11 + ... 4/65.68
c) chứng tỏ rằng 16n + 5 / 24n + 7 là phân số tối giản với mọi n thuộc z
Toán lớp 6
ai tích mình tích lại nh nha
Đúng 0
Bình luận (0)
CMR
16n+5 / 24n +7 là phân số tối giản
gọi d là UCLN(16n+5;24n+7)
Ta có:
[3(16n+5)]-[2(24n+7)] chia hết d
=>[48n+15]-[48n+14] chia hết d
=>1 chia hết d
=>d=1
=>16n+5 và 24n +7 là 2 số nguyên tố cùng nhau
=>16n+5 / 24n +7 là phân số tối giản
Đúng 0
Bình luận (0)
chứng tỏ rằng \(\frac{16n+5}{24n+7}\)là phân số tối giản
Gọi d là ƯCLN(16n+5;24n+7)
=>16n+5 chia hết cho d và 24n+7 chia hết cho d
=>3(16n+5) chia hết cho d và 2(24n+7) chia hết cho d
=>48n+15 chia hết cho d và 48n+14 chia hết cho d
=>(48n+15)-(48n+14) chia hết cho d
=>1 chia hết cho d
=>d=1;ƯCLN(16n+5;24n+7)=1
Vì ƯCLN(16n+5;24n+7)=1 nên 16n+5/24n+7 tối giản
Đúng 0
Bình luận (0)
CMR : 16n+5/24n+7 là ps tối giản
Gọi d = ƯCLN ( 16n + 5 ; 24n + 7 ) => 16n + 5 ⋮ d và 24n + 7 ⋮ d
=> 3.( 16n + 5 ) ⋮ d và 2.( 24n + 7 ) ⋮ d => 48n + 15 ⋮ d và 48n + 14 ⋮ d
=> (48n + 15) - (48n + 14) ⋮ d => d = 1
Vậy phân số 16n + 5 / 24n + 7 tối giản
Đúng 0
Bình luận (0)
gọi ĐLÀ ƯC16n+5\24n+7=
suy ra 16n+1 chia hết cho Đ suy ra 3.(16n+5) chia hết ch Đ
..........24n+7.....................suy ra 2(24n+7)......................
suy ra(48n+15)-(48n+14) CHIA HẾT CHO Đ
suy ra 1 chia hết choĐ và Đ=1
VÌ 16N+5\24N+7 CO ƯC =1suy ra là p\s toi gian
Đúng 0
Bình luận (0)
CM phân số 16n+5/24+7 tối giản với mọi n€N
Gọi UCLN( 16n + 5; 24n + 7) là d.
Ta có:
16n + 5 chia hết cho d => 48n + 15 chia hết cho d ( 1 )
24n + 7 chia hết cho d => 48n + 14 chia hết cho d ( 2 )
Từ (1)(2) ta có: (48n + 15) - (48n +14) chia hết cho d => 1 chia hết cho d => d thuộc U(1) = { -1; 1}
Vậy 16n + 5; 24n + 7 là phân số tối giản.
Đúng 0
Bình luận (0)
Chứng tỏ rằng: 16 n + 5 24 n + 7 là phân số tối giản với mọi n ∈ N