Cho x,y,z thoả mãn Điều kiện
xy+yz+zx=5
Tính giá trị biểu thức: 3x2+3y2+z2
Giúp vs cho 69 tick
NP
Những câu hỏi liên quan
Cho x,y,z thuộc Z biết:
xy+yz+zx=5
Tính 3x2+3y2+z2
giúp với mai thi rồi!
Cho các số thực x, y, z thay đổi và thỏa mãn điều kiện
x
2
+
y
2
+
z
2
1
. Giá trị nhỏ nhất của biểu thức
P
x
y
+
y
z
+
2
x
z...
Đọc tiếp
Cho các số thực x, y, z thay đổi và thỏa mãn điều kiện x 2 + y 2 + z 2 = 1 . Giá trị nhỏ nhất của biểu thức P = x y + y z + 2 x z 2 − 8 x + y + z 2 − x y − y z + 2
A. min P = − 5
B. min P = 5
C. min P = 3
D. min P = − 3
Đáp án D
Ta có C 12 1 . C 10 1 = 120
Khi đó C 12 1 . C 10 1 = 120 . Đặt C 12 1 . C 10 1 = 120
Ta luôn có C 12 1 . C 10 1 = 120
C 12 1 . C 10 1 = 120 Suy ra C 12 1 . C 10 1 = 120
Xét hàm số f t = t 2 − 8 t + 3 trên khoảng − 1 ; + ∞ ,có f ' t = 2 t + 1 2 t + 4 t + 3 2 > 0 ; ∀ t > − 1
Hàm số f(t) liên tục trên − 1 ; + ∞ ⇒ f t đồng biến trên − 1 ; + ∞
Do đó, giá trị nhỏ nhất của f(t) là min − 1 ; + ∞ f t = f − 1 = − 3 . Vậy P min = − 3
Đúng 0
Bình luận (0)
\(\text{cho x,y,z là các số thực khác 0 và thỏa mãn điều kiện xy+yz+zx=0. Tính giá trị của biểu thức A= }\dfrac{x+y}{z}+\dfrac{y+z}{x}+\dfrac{x+z}{y}\)
\(\dfrac{x+y}{z}+\dfrac{y+z}{x}+\dfrac{x+z}{y}=\dfrac{x^2y+xy^2+y^2z+yz^2+x^2z+xz^2}{xyz}=\dfrac{-3xyz}{xyz}=-3\)
đề cho xy+yz+xz=0 nhân cả 2 vế với -z
=>-xyz-\(z^2\left(y+x\right)\)=0
=>-xyz=\(z^2x+z^2y\)
cmtt bạn nhân với -y và -z
=>-3xyz=\(x^2y+xy^2+y^2z+yz^2+x^2z+xz^2\)
Đúng 2
Bình luận (0)
Cho x , y , z > 0 thảo mãn điều kiện x + y + z = a
Xem chi tiết
Tìm giá trị lớn nhất của biểu thức : M = xy + yz + zx
Giải giúp vs :3 lớp 9 nha mấy tình yêu
có: \(x^2+y^2\ge2xy\left(BDTCauchy\right)\)
\(x^2+z^2\ge2xz\)
\(y^2+z^2\ge2yz\)
Cộng vế với vế \(\Rightarrow x^2+y^2+z^2\ge xy+xz+yz\)
\(\Rightarrow\left(x+y+z\right)^2\ge3\left(xy+xz+yz\right)\)
\(\Rightarrow\frac{a^2}{3}\ge xy+xz+yz\)
MaxM=a2/3
Dấu "=" xảy ra <=> x=y=z=1/3a
Đúng 0
Bình luận (0)
Cho x, y, z 0 thỏa mãn xy + yz + zx 1. Tính giá trị của biểu thức
A
x
1
+
y
2
1
+
z
2
1
+
x...
Đọc tiếp
Cho x, y, z > 0 thỏa mãn xy + yz + zx = 1. Tính giá trị của biểu thức
A = x 1 + y 2 1 + z 2 1 + x x + y 1 + z 2 1 + x 2 1 + y 2 + z 1 + x 2 1 + y 2 1 + z 2
A. A = 1
B. A = 3
C. A = 2
D. A = 0
Chọn đáp án C.
Vì x, y ,z > 0 nên x + y > 0; y + z > 0 và x + z > 0
Ta có:
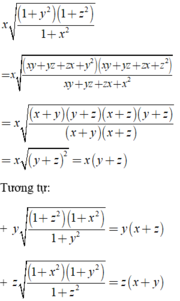
Khi đó
A = x(y + z) + y(x + z) + z(x + y)
= xy + xz + xy + yz + xz + zy = 2(xy + yz + zx) = 2
Đúng 0
Bình luận (0)
Cho x,y,z là các số thực khác 0 thoả mãn xy+yz+xz=0
Tính giá trị của biểu thức
\(M=\frac{yz}{x^2}+\frac{zx}{y^2}+\frac{xy}{z^2}\)
Giúp với nha
Cho ba số x, y, z thỏa mãn các điều kiện x+ y+ z=0 và xy+ yz+ zx = 0
Tính giá trị của biểu thức sau : P = (x - 1)2003 + y2004 + (z + 1)2005
\(0=\left(x+y+z\right)^2=x^2+y^2+z^2+2\left(xy+yz+zx\right)=x^2+y^2+z^2+0\)
\(\Rightarrow x^2+y^2+z^2=0\)
\(\Rightarrow x=y=z=0\)
\(P=\left(-1\right)^{2003}+0^{2004}+1^{2005}=0\)
Đúng 0
Bình luận (0)
Cho các số thực x, y, z thỏa mãn điều kiện
x
-
y
+
z
3
x
2
+
y
2
+...
Đọc tiếp
Cho các số thực x, y, z thỏa mãn điều kiện x - y + z = 3 x 2 + y 2 + z 2 = 5 . Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của biểu thức P = x + y - 2 z + 2 . Tính M + m
A. M + m = 2
B. M + m = 4 3 3
C. M + m = 4
D. M + m = 4 3 6
Cho các só thực x, y, z thỏa mãn điều kiện
x
-
y
+
z
3
x
2
+
y
2
+...
Đọc tiếp
Cho các só thực x, y, z thỏa mãn điều kiện x - y + z = 3 x 2 + y 2 + z 2 = 5 . Hỏi biểu thức P = x + y - 2 z + 2 có thể nhận bao nhiêu giá trị nguyên?
A. 2
B. 1
C. 3
D. 4
Chọn đáp án A
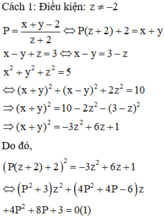
Do đó, P có thể nhận các giá trị nguyên là 0; -1
STUDY TIP |
Trong biểu thức P vai trò của z khác x, y do đó, ta tìm cách rút x, y theo z từ điều kiện ban đầu. Từ đó quy về phương trình ẩn z và tìm điều kiện để phương trình có nghiệm |
Phương trình (2), (3) là các phương trình mặt phẳng
Hai mặt phẳng này cắt nhau theo giao tuyến d có vecto chỉ phương là
Phương trình (4) là phương trình mặt cầu (S) có tâm O(0;0;0) bán kính R = 5
X, y, z tồn tại khi và chỉ khi d cắt (S)
Do đó P có thể nhận các giá trị nguyên là 0; -1
STUDY TIP |
Các biểu thức liên hệ giữa x, y, z có dạng phương trình mặt phẳng, mặt cầu. Từ đó giúp ta nghĩ đến việc xét vị trí tương dối giữa mặt cầu, với đường thẳng và mặt phẳng |
Đúng 0
Bình luận (0)