Cho biểu thức M=(√x√x−x −√x+21−x ) với (x>0;x≠1)
a. Rút gọn biểu thức M
b. tìm tất cả các giá trị của x để biểu thức M nhận giá trị nguyên
Cho biểu thức M=(√x√x−x −√x+21−x ) với (x>0;x≠1)
a. Rút gọn biểu thức M
b. tìm tất cả các giá trị của x để biểu thức M nhận giá trị nguyên
Rút gọn biểu thức: B = 4 x + 1 + 2 1 - x - x - 5 x - 1 với x ≥ 0, x ≠ 1
A. x + 1 x + 1
B. 2 x + 1
C. x + 1
D. 1 x + 1
Câu 4: Cho biểu thức: \(M=\left(\dfrac{x-\sqrt{x}}{\sqrt{x}-1}-\dfrac{\sqrt{x}+1}{x+\sqrt{x}}\right):\dfrac{\sqrt{x}+1}{x}\) với \(x>0,\) \(x\) ≠ 1
a. Điều kiện biểu thức có nghĩa
b. Rút gọn M
c. Tìm \(x\) để M < 0
\(a,ĐK:x>0;x\ne1\\ b,M=\left[\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}-\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\right]\cdot\dfrac{\sqrt{x}}{\sqrt{x}+1}\\ M=\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)\cdot\dfrac{\sqrt{x}}{\sqrt{x}+1}=\dfrac{x-1}{\sqrt{x}}\cdot\dfrac{x}{\sqrt{x}+1}=\sqrt{x}-1\\ c,M< 0\Leftrightarrow\sqrt{x}< 1\Leftrightarrow0< x< 1\)
Cho biểu thức:
M = x + 2 x - 3 + x + 1 x - 2 - 3 . x - 1 x - 5 x + 6 với x ≥ 0 , x ≠ 4 , x ≠ 9
a) Thu gọn biểu thức M.
Cho biểu thức:\(M=\left(\dfrac{3}{\sqrt{x}+3}+\dfrac{x+9}{x-9}\right):\left(\dfrac{2\sqrt{x}-5}{x-3\sqrt{x}}-\dfrac{1}{\sqrt{x}}\right)\) với: \(x>0;x\ne9\)
|
1/ Rút gọn biểu thức M |
2/ Tìm x sao cho M < 0 |
|
3/ Tìm số tự nhiên x để M nguyên âm |
4/ Cho x > 4. Tìm giá trị nhỏ nhất của M |
a) \(M=\left(\dfrac{3}{\sqrt{x}+3}+\dfrac{x+9}{x-9}\right):\left(\dfrac{2\sqrt{x}-5}{x-3\sqrt{x}}-\dfrac{1}{\sqrt{x}}\right)\)
\(=\dfrac{3.\left(\sqrt{x}-3\right)+x+9}{\left(\sqrt{x}-3\right).\left(\sqrt{x}+3\right)}:\dfrac{2\sqrt{x}-5-\left(\sqrt{x}-3\right)}{\sqrt{x}.\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x+3\sqrt{x}}{\left(\sqrt{x}-3\right).\left(\sqrt{x}+3\right)}:\dfrac{\sqrt{x}-2}{\sqrt{x}.\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}.\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right).\left(\sqrt{x}+3\right)}.\dfrac{\sqrt{x}.\left(\sqrt{x}-3\right)}{\sqrt{x}-2}=\dfrac{x}{\sqrt{x}-2}\)
b) \(M< 0\Leftrightarrow\sqrt{x}-2< 0\Leftrightarrow x< 4\)
Kết hợp điều kiện ta được \(0< x< 4\) thì M < 0
c) Từ câu b ta có M < 0 \(\Leftrightarrow0< x< 4\)
nên \(x\inℤ\) để M nguyên âm <=> \(x\in\left\{1;2;3\right\}\)
Thay lần lượt các giá trị vào M được x = 1 thỏa
d) \(M=\dfrac{x}{\sqrt{x}-2}=\sqrt{x}+2+\dfrac{4}{\sqrt{x}-2}=\left(\sqrt{x}-2+\dfrac{4}{\sqrt{x}-2}\right)+4\)
Vì x > 4 nên \(\sqrt{x}-2>0\)
Áp dụng BĐT Cauchy ta có
\(M=\left(\sqrt{x}-2+\dfrac{4}{\sqrt{x}-2}\right)+4\ge2\sqrt{\left(\sqrt{x}-2\right).\dfrac{4}{\sqrt{x}-2}}+4=8\)
Dấu "=" xảy ra khi \(\sqrt{x}-2=\dfrac{4}{\sqrt{x}-2}\Leftrightarrow x=16\left(tm\right)\)
1) \(M=\left(\dfrac{3}{\sqrt[]{x}+3}+\dfrac{x+9}{x-9}\right):\left(\dfrac{2\sqrt[]{x}-5}{x-3\sqrt[]{x}}-\dfrac{1}{\sqrt[]{x}}\right)\left(x>0;x\ne9\right)\)
\(\Leftrightarrow M=\left(\dfrac{3\left(\sqrt[]{x}-3\right)}{\left(\sqrt[]{x}+3\right)\left(\sqrt[]{x}-3\right)}+\dfrac{x+9}{x-9}\right):\left(\dfrac{2\sqrt[]{x}-5}{\sqrt[]{x}\left(\sqrt[]{x}-3\right)}-\dfrac{1}{\sqrt[]{x}}\right)\)
\(\Leftrightarrow M=\left(\dfrac{3\sqrt[]{x}-9+x+9}{x-9}\right):\left(\dfrac{2\sqrt[]{x}-5-\left(\sqrt[]{x}-3\right)}{\sqrt[]{x}\left(\sqrt[]{x}-3\right)}\right)\)
\(\Leftrightarrow M=\left(\dfrac{3\sqrt[]{x}+x}{x-9}\right):\left(\dfrac{2\sqrt[]{x}-5-\sqrt[]{x}+3}{\sqrt[]{x}\left(\sqrt[]{x}-3\right)}\right)\)
\(\Leftrightarrow M=\left(\dfrac{\sqrt[]{x}\left(\sqrt[]{x}+3\right)}{x-9}\right):\left(\dfrac{\sqrt[]{x}-2}{\sqrt[]{x}\left(\sqrt[]{x}-3\right)}\right)\)
\(\Leftrightarrow M=\left(\dfrac{\sqrt[]{x}}{\sqrt[]{x}-3}\right):\left(\dfrac{\sqrt[]{x}-2}{\sqrt[]{x}\left(\sqrt[]{x}-3\right)}\right)\)
\(\Leftrightarrow M=\dfrac{\sqrt[]{x}}{\sqrt[]{x}-3}.\dfrac{\sqrt[]{x}\left(\sqrt[]{x}-3\right)}{\sqrt[]{x}-2}\)
\(\Leftrightarrow M=\dfrac{x}{\sqrt[]{x}-2}\)
2) Để \(M< 0\) khi và chỉ chi
\(M=\dfrac{x}{\sqrt[]{x}-2}< 0\left(1\right)\)
Nghiệm của tử là \(x=0\)
Nghiệm của mẫu \(\sqrt[]{x}-2=0\Leftrightarrow\sqrt[]{x}=2\Leftrightarrow x=4\)
Lập bảng xét dấu... ta được
\(\left(1\right)\Leftrightarrow0< x< 4\)
3) \(M=\dfrac{x}{\sqrt[]{x}-2}\inℤ^-\)
\(\Leftrightarrow x⋮\sqrt[]{x}-2\)
\(\Leftrightarrow x-\sqrt[]{x}\left(\sqrt[]{x}-2\right)⋮\sqrt[]{x}-2\)
\(\Leftrightarrow x-x+2\sqrt[]{x}⋮\sqrt[]{x}-2\)
\(\Leftrightarrow2\sqrt[]{x}⋮\sqrt[]{x}-2\)
\(\Leftrightarrow2\sqrt[]{x}-2\left(\sqrt[]{x}-2\right)⋮\sqrt[]{x}-2\)
\(\Leftrightarrow2\sqrt[]{x}-2\sqrt[]{x}+4⋮\sqrt[]{x}-2\)
\(\Leftrightarrow4⋮\sqrt[]{x}-2\)
\(\Leftrightarrow\sqrt[]{x}-2\in\left\{-1;-2;-4\right\}\)
\(\Leftrightarrow x\in\left\{1;0\right\}\)
Cho biểu thức :
A = 15 x - 11 x + 2 x - 3 + 3 x - 2 1 - x - 3 x + 3 x ≥ 0 ; x ≠ 1
a) Thu gọn biểu thức A.
x + 2 x - 3 = x - x + 3 x - 3 = x ( x - 1) + 3( x - 1) = ( x - 1)( x + 3)
a) Với điểu kiện x ≥ 0; x ≠ 1 ta có:
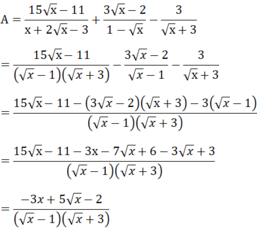
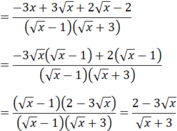
Cho biểu thức M=(\(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\) -\(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)):\(\dfrac{x}{x-\sqrt{x}}\)
( với x>0 và x≠ 1)
a)Rút gọn biểu thức M
b)Tìm giá trị của x sao cho M> 1
a) M = \(\dfrac{\left(\sqrt{x}+1\right)^2-\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\). \(\dfrac{x-\sqrt{x}}{x}\) ( x>0)
M = \(\dfrac{4\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\). \(\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{x}\)
M = \(\dfrac{4}{\sqrt{x}+1}\)
b) M>1 => 4 > \(\sqrt{x}\) + 1 > 0
=> 3 > \(\sqrt{x}\) > -1
=> 9>x>0
Đúng thì like giúp mik nha bạn. Thx
Cho hai biểu thức A=\(\dfrac{\sqrt{X}+2}{x-\sqrt{x}}\) và B=\(\dfrac{1}{\sqrt{x}-1}-\dfrac{\sqrt{x}}{\sqrt{x}+1}+\dfrac{x+3}{x-1}\) với x>0,x≠1
a. thu gọn biểu thức M=A:B
b.tìm x sao cho M>1
\(a,M=\left(\dfrac{\sqrt{x}+2}{x-\sqrt{x}}\right):\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{\sqrt{x}}{\sqrt{x}+1}+\dfrac{x+3}{x-1}\right)\\ =\left(\dfrac{\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\left(\dfrac{\sqrt{x}+1-\sqrt{x}\left(\sqrt{x}-1\right)+x+3}{x-1}\right)\\ =\dfrac{\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{x-1}{\sqrt{x}+1-x+\sqrt{x}+x+3}\\ =\dfrac{\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{x-1}{2\sqrt{x}+4}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{x-1}{2\left(\sqrt{x}+2\right)}\\ =\dfrac{\sqrt{x}+1}{2\sqrt{x}}\)
`b,` Để `M>1` Thì :
\(\dfrac{\sqrt{x}+1}{2\sqrt{x}}>1\\ \Leftrightarrow\dfrac{\sqrt{x}+1}{2\sqrt{x}}-1>0\\ \Leftrightarrow\dfrac{\sqrt{x}+1-2\sqrt{x}}{2\sqrt{x}}>0\\ \Leftrightarrow\dfrac{-\sqrt{x}+1}{2\sqrt{x}}>0\)
\(\Leftrightarrow-\sqrt{x}+1>0\) `(` Vì \(2\sqrt{x}>0\) do \(x>0\) `)`
\(\Leftrightarrow-\sqrt{x}>-1\\ \Rightarrow x< 1\)
Cho biểu thức A=\(\dfrac{\sqrt{x}}{\sqrt{x}-1}\)và B=\(\dfrac{3x}{x-2\sqrt{x}+1}-\dfrac{\sqrt{x}}{\sqrt{x}-1}\)với x>0,x\(\ne\)1
1.Tính giá trị biểu thức khi A=0,09
2.Rút gọn biểu thức B và M=B:A
3.Tìm giá trị x để biểu thức M<1
1) Sửa đề: x=0,09
Thay x=0,09 vào A, ta được:
\(A=\dfrac{\sqrt{0.09}}{\sqrt{0.09}-1}=\dfrac{0.3}{0.3-1}=\dfrac{0.3}{-0.7}=\dfrac{-3}{7}\)