với số thực tùy ý căn bậc 2 sô học của \(\left(x-2\right)^2\) là
DK
Những câu hỏi liên quan
Hoạt động 2
a) Với a là số thực không âm, nêu định nghĩa căn bậc hai của a
b) Với a là số thực tùy ý, nêu định nghĩa căn bậc ba của a
a: căn bậc hai của một số a không âm là một số x thỏa mãn \(x^2=a\)
b: Căn bậc hai của một số a bất kỳ là một số x sao cho x thỏa mãn \(x^3=a\)
Đúng 0
Bình luận (0)
Hoạt động 1
a) Cho n là một số nguyên dương. Với a là số thực tùy ý, nêu định nghĩa lũy thừa bậc n của a
b) Với a là số thực tùy ý khác 0, nêu quy ước xác định lũy thừa bậc 0 của a.
a: Cho \(a\in R;n\in Z^+\) thì \(a^n=a\cdot a\cdot...\cdot a\)(n chữ số a)
b: \(a^0=1\)
Đúng 0
Bình luận (0)
Trong các số \(\sqrt{\left(-5\right)^2};\sqrt{5^2};-\sqrt{5^2};-\sqrt{\left(-5\right)^2}\), số nào là căn bậc hai số học của 25 ?
a) Quan sát Hình 21 và cho biết dấu của tam thức bậc hai fleft( x right) {x^2} + 3x + 2 tùy theo các khoảng của x.b) Quan sát Hình 22 và cho biết dấu của tam thức bậc hai fleft( x right) - {x^2} + 4x - 3 tùy theo các khoảng của x.c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai fleft( x right) a{x^2} + bx + cleft( {a ne 0} right) với dấu của hệ số tùy theo các khoảng của x trong trường hợp Delta 0.
Đọc tiếp
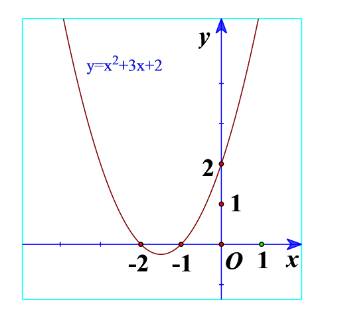
a) Quan sát Hình 21 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = {x^2} + 3x + 2\) tùy theo các khoảng của x.
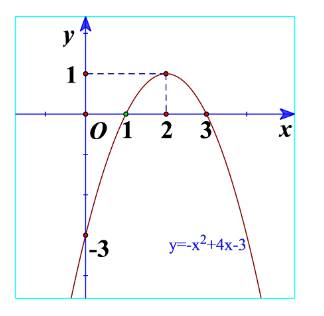
b) Quan sát Hình 22 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = - {x^2} + 4x - 3\) tùy theo các khoảng của x.
c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) với dấu của hệ số tùy theo các khoảng của x trong trường hợp \(\Delta > 0\).
a) Ta thấy trên \(\left( { - \infty ; - 2} \right)\): Đồ thị nằm trên trục hoành
=> \(f\left( x \right) = {x^2} + 3x + 2 > 0\)\(\forall x \in \left( { - \infty ; - 2} \right)\)
Trên \(\left( { - 2; - 1} \right)\): Đồ thị nằm dưới trục hoành
=> \(f\left( x \right) = {x^2} + 3x + 2 < 0\)\(\forall x \in \left( { - 2; - 1} \right)\)
Trên \(\left( { - 1; + \infty } \right)\): Đồ thị nằm trên trục hoành
=> \(f\left( x \right) = {x^2} + 3x + 2 > 0\)\(\forall x \in \left( { - 1; + \infty } \right)\)
b)
Trên \(\left( { - \infty ;1} \right)\): Đồ thị nằm dưới trục hoành
=> \(f\left( x \right) = - {x^2} + 4x - 3 < 0\)\(\forall x \in \left( { - \infty ;1} \right)\)
Trên \(\left( {1;3} \right)\): Đồ thị nằm trên trục hoành
=> \(f\left( x \right) = - {x^2} + 4x - 3 > 0\)\(\forall x \in \left( {1;3} \right)\)
Trên \(\left( {3; + \infty } \right)\): Đồ thị nằm dưới trục hoành
=> \(f\left( x \right) = - {x^2} + 4x - 3 < 0\)\(\forall x \in \left( {3; + \infty } \right)\)
c) Nếu \(\Delta > 0\) thì \(f\left( x \right)\) cùng dấu vưới hệ số a với mọi x thuộc các khoảng \(\left( { - \infty ;{x_1}} \right)\) và \(\left( {{x_2}; + \infty } \right)\); \(f\left( x \right)\) trái dấu với hệ số a với mọi x thuộc khoảng \(\left( {{x_1};{x_2}} \right)\), trong đó \({x_1},{x_2}\) là hai nghiệm của \(f\left( x \right)\) và \({x_1} < {x_2}\).
Đúng 0
Bình luận (0)
Cho a,B,C LÀ CÁC Số THực DƯƠNG TÙY Ý. cmr:
\(\left(a+b+c\right)^3\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)\le27a^2b^2c^2\)
Đặt \(a+b-c=x;b+c-a=y;a+c-b=z\)
BĐT <=> \(\left(x+y+z\right)^3xyz\le27.\left(\frac{x+z}{2}\right)^2\left(\frac{y+z}{2}\right)^2\left(\frac{x+y}{2}\right)^2\)
<=> \(64xyz\left(x+y+z\right)^3\le\left[\left(x+y\right)\left(y+z\right)\left(x+z\right)\right]^2\)(1)
Xét \(\left(x+y\right)\left(y+z\right)\left(x+z\right)\ge\frac{8}{9}\left(x+y+z\right)\left(xy+yz+xz\right)\)
<=> \(9\left[xy\left(x+y\right)+yz\left(y+z\right)+xz\left(x+z\right)+2xyz\right]\ge8\left[xy\left(x+y\right)+...+3xyz\right]\)
<=> \(xy\left(x+y\right)+xz\left(x+z\right)+yz\left(y+z\right)\ge6xyz\)(luôn đúng )
vì \(VT\ge3\sqrt[3]{x^2y^2z^2.\left(x+y\right)\left(y+z\right)\left(x+z\right)}\ge6xyz\)
Khi đó BĐT (1)
<=> \(64.xyz\left(x+y+z\right)^3\le27\left[\frac{8}{9}\left(x+y+z\right)\left(xy+yz+xz\right)\right]^2\)
<=> \(3xyz\left(x+y+z\right)\le\left(xy+yz+xz\right)^2\)
<=> \(x^2y^2+y^2z^2+x^2z^2\ge xyz\left(x+y+z\right)\)(BĐT Cosi)
=> BĐT được Cm
Dấu bằng xảy ra khi a=b=c
Mình có cách khác
bđt đồng bật nên t chuẩn hóa \(a+b+c=1\)
Ta biến doi vế trái về: \(\left[\left(a+b\right)^2-c^2\right]\left[\left(b+c\right)^2-a^2\right]\left[\left(c+a\right)^2-b^2\right]\)
\(=\left[\left(1-c\right)^2-c^2\right]\left[\left(1-a\right)^2-a^2\right]\left[\left(1-b\right)^2-b^2\right]\)
Giờ ta cần chứng minh:\(\left[\left(1-c\right)^2-c^2\right]\left[\left(1-a\right)^2-a^2\right]\left[\left(1-b^2\right)-b^2\right]\le27a^2b^2c^2\)
Ta xét :\(0< a,b,c< \frac{1}{3}\)(*)
\(\Rightarrow a+b+c< 1\)
vì \(a+b+c=1\)nên (*) vô lý
Ta xét:\(\frac{1}{3}\le a,b,c< 1\)
Đến đây ta thấy giữa các biến có sự riêng biệt nên ta xét:
\(3a^2-\left[\left(1-a\right)^2-a^2\right]=\left(3a-1\right)\left(a+1\right)\ge0\)
\(\Rightarrow3a^2\ge\left(1-a\right)^2-a^2\)
Tương tự:\(3b^2\ge\left(1-b\right)^2-b^2\)
\(3c^2\ge\left(1-c\right)^2-c^2\)
nhan các vế bđt lại với nhau ta có điều phải chứng minh
Đến đây ta có thể suy ra điều phải chứng minh
vài lời nhắn:
Mình không chắt về cách xét của mình nữa
Nub
Đoạn bạn xét \(\frac{1}{3}\le a,b,c< 1\)mà \(a+b+c=1\)
thì chẳng khác nào bạn cho \(a=b=c=\frac{1}{3}\)
vì vậy đến đoạn đó bạn không xét như vậy được
Xem thêm câu trả lời
1. Tính \(\left[a+\left(-b\right)\right]^2\) (với a, b là các số tùy ý)
2. Tính \(\left(2x-3y\right)^2\)
2) (2x - 3y)2
= (2x)2 - 2.2x.3y + ( 3y)2
= 4x2 - 12xy + 9y2
t i c k nhé!!!! 4645757878769698700795783537742637645756756756765
Đúng 0
Bình luận (0)
1) giả sử a = 3x ; b = 5y ta có:
[3x + (-2y)]2
= (3x)2 + 2.3x.(-2y) + (-2y)2
= 9x2 - 12xy + 4y2
= (3x - 2y)2
2) (2x - 3y)2
= (2x)2 - 2.2x.3y + (3y)2
= 4x2 - 12xy + 9y2
t i c k nha!!!!! 576767868658769769765474745735733462464575687687685789587
Đúng 0
Bình luận (0)
Tìm gtnn của căn bậc hai (x^2+(y+1)^2)+ căn bậc hai(x^2+(y-3)^2)
x;y là số thực
2x-y=2
Bạn nên gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề và hỗ trợ tốt hơn nhé.
Đúng 0
Bình luận (0)
cho x,y,z là các số thực thỏa mãn -1<=x,y,z <=1 và x+y+z =o. tìm GTNN biểu thức :P=căn bậc 2 1+x+y^2 +căn bậc 2 của 1+y+z^2 + căn bậc 2 của 1+z+x^2
tìm căn bậc 2 số học của 54 từ đó suy ra căn bậc 2 của 54
tìm căn bậc 2 số học của 129 từ đó suy ra căn bậc 2 của 129
tìm căn bậc 2 số học của 322 từ đó suy ra căn bậc 2 của 322



