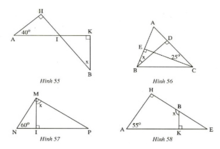
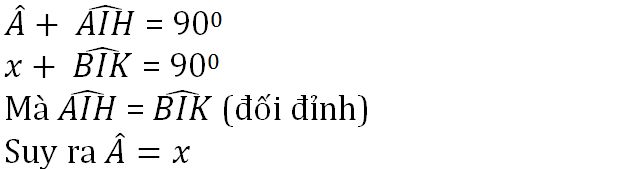tính số đo x ở hình 57 ; 58 
VT
Những câu hỏi liên quan
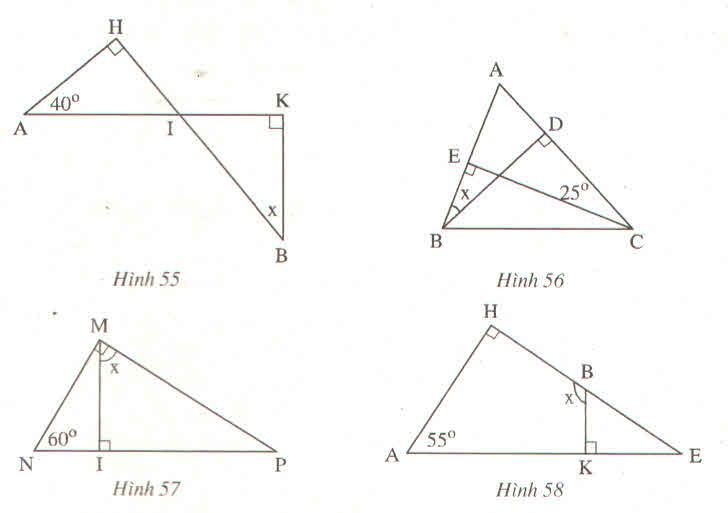
Tìm số đo x ở các hình 55, 56, 57, 58.
Áp dụng tính chất “Trong tam giác vuông, hai góc nhọn phụ nhau” ta có:
+ Hình 55:

+ Hình 56:

+ Hình 57 :

+ Hình 58:
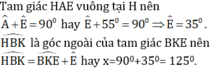
Đúng 0
Bình luận (0)
Tính số đo x của góc AOB ở hình dưới, cho biết a//b.
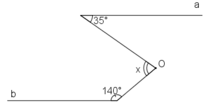
Qua O kẻ đường thẳng c // a // b.
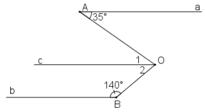
Vì a//c nên ∠A = ∠(O1) (hai góc so le trong)
Mà ∠A = 35o nên ∠(O1) = 35o
Vì b // c nên ∠(O2) + ∠B = 180o (hai góc trong cùng phía bù nhau)
⇒ ∠(O2) = 180o - ∠B
Mà ∠B = 140o ⇒ ∠(O2) = 180o – 140o = 40o
x = ∠(AOB) = ∠(O1) + ∠(O2) = 35o + 40o = 75o.
Đúng 0
Bình luận (0)
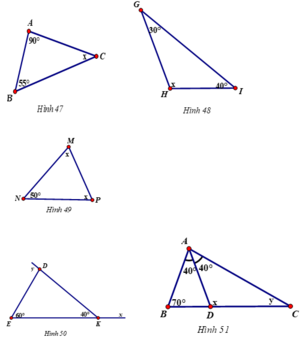
Tính các số đo x, y ở các hình 47, 48, 49, 50, 51.
Áp dụng định lý tổng ba góc trong một tam giác bằng 180º ta có:
- Hình 47
x + 90o + 55o = 180o
x = 180o - 90o - 55o
x = 35o
- Hình 48
x + 30o + 40o = 180o
x = 180o - 30o - 40o
x = 110o
- Hình 49
x + x + 50o = 180o
2x = 180o - 50o
x = 65o
Áp dụng định lý góc ngoài của tam giác ta có:
- Hình 50
y = 60o + 40o
y = 100o
x + 40o = 180o (2 góc kề bù)
x = 140o
- Hình 51
Áp dụng định lý góc ngoài trong tam giác ABD có: x = 70º + 40º = 110º
Áp dụng định lý tổng ba góc trong tam giác ADC có:
y + 110º + 40º = 180º ⇒ y = 30º.
Đúng 0
Bình luận (0)
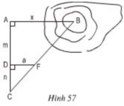
Để đo khoảng cách giữa hai điểm A và B, trong đó B không tới được, người ta tiến hành đo và tính khoảng cách AB như hình 57; AB // DF; AD = m;DC = n; DF = a.
a) Em hãy nói rõ cách đo như thế nào.
b) Tính độ dài x của khoảng cách AB.
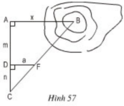
a) Cách đo:
+ Tạo một tia Ay trên mặt đất vuông góc với tia AB.
+ Trên tia Ay lấy điểm C bất kì.
+ Chọn điểm F sao cho F nằm giữa B và C.
+ Từ F hạ FD vuông góc với AC (D nằm trên AC).
+ Đo các cạnh AD, DC, DF ta tính được khoảng cách AB.
b) ΔCDF 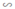 ΔCAB (do DF // AB)
ΔCAB (do DF // AB)
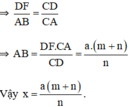
Đúng 0
Bình luận (0)
Để đo khoảng cách giữa hai điểm A và B, trong đó B không tới được, người ta tiến hành đo và tính khoảng cách AB như hình 57; AB // DF; AD = m;DC = n; DF = a.
a) Em hãy nói rõ cách đo như thế nào.
b) Tính độ dài x của khoảng cách AB.
a) Cách đo:
+ Tạo một tia Ay trên mặt đất vuông góc với tia AB.
+ Trên tia Ay lấy điểm C bất kì.
+ Chọn điểm F sao cho F nằm giữa B và C.
+ Từ F hạ FD vuông góc với AC (D nằm trên AC).
+ Đo các cạnh AD, DC, DF ta tính được khoảng cách AB.
b) ΔCDF 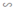 ΔCAB (do DF // AB)
ΔCAB (do DF // AB)
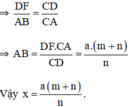
Đúng 0
Bình luận (0)
Tìm số đo x trên hình 55, 56, 57, 58 ?
Hình 55:
Ta có ∠A + ∠AIH = 900 (Vì tam giác AHI cân tại H) ⇒∠AIH = 900 – 400 = 500
mà ∠AIH = ∠BIK( 2 góc đối đỉnh) ⇒∠BIK = 500
Ta lại có: ∠IBK +∠BIK = 900 (Vì tam giác IKB cân tại K)
⇒ ∠IBK = 900 – 500 = 400
⇒ x = 400
Hình 56:
Các em có thể giải theo cách của bài 55 tuy nhiên là hơi dài và chúng ta có cách khác làm nhanh hơn. (Áp dụng hình 56 và các hình sau nhé)
Ta có :
Xét tam giác ABD cân tại D ta có ∠ABD + ∠BAD = 900
Xét tam giác ACE cân tại E ta có ∠ACE + ∠EAC = 900
Mà ta có ∠BAD cũng chính là góc ∠EAC
Suy ra ∠ABD = ∠ACE = 250
Vậy ∠ABD = 250 => x = 250
Hình 57:
Xét tam giác MNP vuông tại M ⇒ ∠MNP+ ∠MPN = 900
⇔ 600 + ∠MPN = 900
⇒ ∠MPN = 900 – 600 = 300
Tiếp tục xét tam giác IMP vuông tại I ⇒ ∠IMP + ∠IPM = 900
⇔ ∠IMP + 300 = 900 ( vì∠IPM = ∠MPN )
⇒∠IMP = 900 – 300 = 600
Vậy ∠IMP = 600 => x = 600
Hình 58:
Ta có
Xét tam gác HAE vuông tại H nên ta có ∠HEA = 900 – ∠HAE = 900 – 550 = 350
hay chính là góc ∠BEK = 350
Ta có: ∠HBK = ∠BEK + ∠BKE (Góc ngoài tam giác BKE)
⇒ ∠HBK = 350+ 900 = 1250
Vậy x = 1250
Đúng 2
Bình luận (1)
Hình 55:
Ta có ∠A + ∠AIH = 900 (Vì tam giác AHI cân tại H) ⇒∠AIH = 900 – 400 = 500
mà ∠AIH = ∠BIK( 2 góc đối đỉnh) ⇒∠BIK = 500
Ta lại có: ∠IBK +∠BIK = 900 (Vì tam giác IKB cân tại K)
⇒ ∠IBK = 900 – 500 = 400
⇒ x = 400
Hình 56:
Ta có :
Xét tam giác ABD cân tại D ta có ∠ABD + ∠BAD = 900
Xét tam giác ACE cân tại E ta có ∠ACE + ∠EAC = 900
Mà ta có ∠BAD cũng chính là góc ∠EAC
Suy ra ∠ABD = ∠ACE = 250
Vậy ∠ABD = 250 => x = 250
Hình 57:
Xét tam giác MNP vuông tại M ⇒ ∠MNP+ ∠MPN = 900
⇔ 600 + ∠MPN = 900
⇒ ∠MPN = 900 – 600 = 300
Tiếp tục xét tam giác IMP vuông tại I ⇒ ∠IMP + ∠IPM = 900
⇔ ∠IMP + 300 = 900 ( vì∠IPM = ∠MPN )
⇒∠IMP = 900 – 300 = 600
Vậy ∠IMP = 600 => x = 600
Hình 58:
Ta có
Xét tam gác HAE vuông tại H nên ta có ∠HEA = 900 – ∠HAE = 900 – 550 = 350
hay chính là góc ∠BEK = 350
Ta có: ∠HBK = ∠BEK + ∠BKE (Góc ngoài tam giác BKE)
⇒ ∠HBK = 350+ 900 = 1250
Vậy x = 1250
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
Tính số đo x của góc O ở hình 8, cho biết a // b:(SBT)
Cho hình thang ABCD có cạnh AD vuông góc với hai đáy AB và CD. Số đo góc ở đỉnh B gấp đôi số đo góc ở đỉnh C. Tính số đo các góc của hình thang đó.

Vì AD vuông góc với hai đáy AB và CD nên \(\widehat{A}=\widehat{D}=90^0\)
Vì ABCD có 2 đáy AB,CD nên AB // CD. Do đó, \(\widehat B + \widehat C = 180^\circ \) ( 2 góc trong cùng phía)
Mặt khác:
\(\begin{array}{l}\widehat B = 2.\widehat C\\ \Rightarrow 2.\widehat C + \widehat C = 180^\circ \\ \Rightarrow 3.\widehat C = 180^\circ \\ \Rightarrow \widehat C = 180^\circ :3 = 60^\circ \end{array}\)
\(\Rightarrow \widehat B = 2. \widehat{C}=2.60^0=120^0\)
Vậy \(\widehat{A}=\widehat{D}=90^0; \widehat B = 120^0; \widehat C =60^0\)
Đúng 0
Bình luận (0)
Xem hình 7. Tính số đo của góc ở tâm AOB và số đo cung lớn AB.