Giải BT Bản Đồ lớp 7 bài 4 Thực hành giúp mình được ko, cảm ơn nhiều nha!
MM
Những câu hỏi liên quan
Có bạn nào biết làm bài này thì giúp mình nha mình đang cần gấp trước 4 giờ mình cảm ơn nhiều (KO dùng hình bình hành, đường cao, tam giác cân, đường trung tuyến hay các kiến thức lớp 8) à thầy mfinh bảo tam giác cân cũng được nhưng phải nói khác đi nhưng thực chất là tam giác ân

Có bạn nào biết làm bài này thì giúp mình nha mình đang cần gấp trước 4 giờ mình cảm ơn nhiều (KO dùng hình bình hành, đường cao, tam giác cân, đường trung tuyến hay các kiến thức lớp 8) à thầy mfinh bảo tam giác cân cũng được nhưng phải nói khác đi nhưng thực chất là tam giác ân

\(a,\left\{{}\begin{matrix}AC=AH\left(GT\right)\\AB.chung\\\widehat{CAB}=\widehat{BAH}\left(=90^0\right)\end{matrix}\right.\Rightarrow\Delta ACB=\Delta AHB\left(c.g.c\right)\)
\(b,\left\{{}\begin{matrix}\widehat{ACB}=\widehat{CBK}\left(so.le.trong\right)\\\widehat{ABC}=\widehat{BCK}\left(so.le.trong\right)\\BC.chung\end{matrix}\right.\Rightarrow\Delta ABC=\Delta KCB\left(g.c.g\right)\Rightarrow AC=BK\left(2.cạnh.tương.ứng\right)\)
\(c,CH=AC+AH=2AC=2AB=BM\\ \left\{{}\begin{matrix}CK//AB\\AB\perp AC\end{matrix}\right.\Rightarrow CK\perp AC\Rightarrow\widehat{ACK}=90^0\\ \left\{{}\begin{matrix}BK//AC\\AC\perp AB\end{matrix}\right.\Rightarrow KB\perp AB\Rightarrow\widehat{ABK}=90^0\\ \left\{{}\begin{matrix}\widehat{ACK}=\widehat{ABK}\left(=90^0\right)\\CH=BM\left(cm.trên\right)\\AC=BK\left(cm.trên\right)\end{matrix}\right.\Rightarrow\Delta CHK=\Delta BMK\left(c.g.c\right)\)
\(d,\Delta CHK=\Delta BMK\left(cm.trên\right)\\ \Rightarrow\widehat{CKH}=\widehat{BKM}\Rightarrow\widehat{CKH}+\widehat{HKB}=\widehat{BKM}+\widehat{HKB}\\ \Rightarrow\widehat{CKB}=\widehat{HKM}\\ \Rightarrow\widehat{BAC}=\widehat{HKM}\left(\Delta ABC=\Delta KCB.nên.\widehat{CKB}=\widehat{BAC}\right)\\ \Rightarrow\widehat{HKM}=90^0\Rightarrow HK\perp KM\)
Đúng 2
Bình luận (1)
Bạn nào học lớp 5 thì giai giúp mình thực hành toán lớp 5 tiết 101 trang 12 giải bai 1 hoặc 2 cũng được nếu giải cả 2 bài thì càng tốt
Cảm ơn các bạn nhiều minh hứa sẽ tục cho bạn nào làm xong trước
Có bạn nào biết làm bài này thì giúp mình nha mình đang cần gấp trước 3 giờ mình cảm ơn nhiều (KO dùng hình bình hành, đường cao, tam giác cân, đường trung tuyến hay các kiến thức lớp 8)

Toán lớp 7 này e ko bt lm ạ,mà e đang cần,ai giúp e giải chi tiết dễ hiểu đc ko ạ,e cảm ơn nhiều lắm ạ!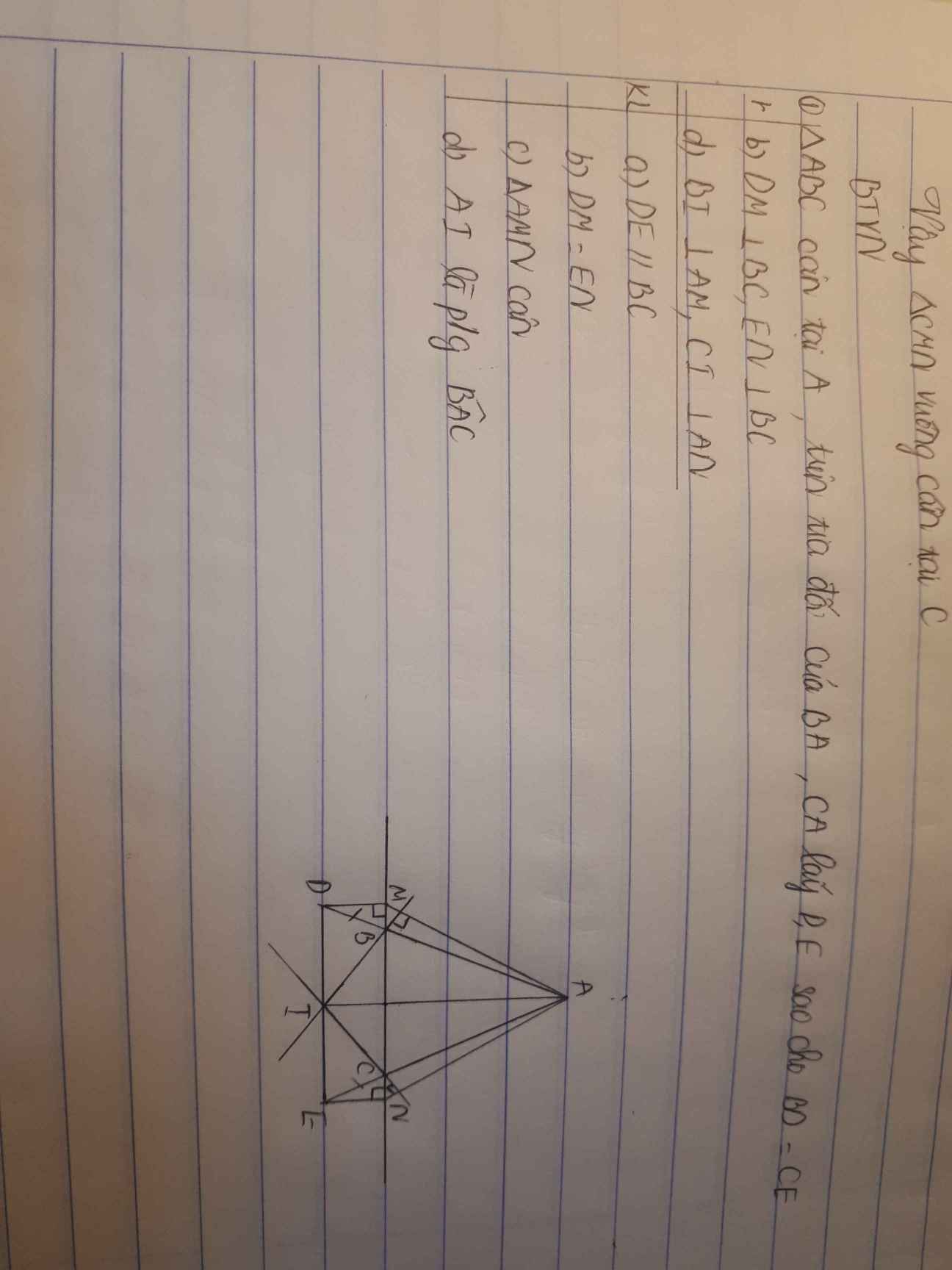
Có bạn nào biết làm bài này thì giúp mình nha mình đang cần gấp trước 4 giờ( rất gấp rồi chỉ còn 2 tiếng) mình cảm ơn nhiều (KO dùng hình bình hành, đường cao, tam giác cân, đường trung tuyến hay các kiến thức lớp 8) à thầy mfinh bảo tam giác cân cũng được nhưng phải nói khác đi nhưng thực chất là tam giác cân
Đọc tiếp
Có bạn nào biết làm bài này thì giúp mình nha mình đang cần gấp trước 4 giờ( rất gấp rồi chỉ còn 2 tiếng) mình cảm ơn nhiều (KO dùng hình bình hành, đường cao, tam giác cân, đường trung tuyến hay các kiến thức lớp 8) à thầy mfinh bảo tam giác cân cũng được nhưng phải nói khác đi nhưng thực chất là tam giác cân

Bạn nào học lớp 7 giúp mình với ( bài 4 : THực hành)
Giúp mình các câu hỏi nhé! Mình ko chụp được hình nên mới phải làm thế này , mong các bạn thông cảm
GIải hộ mình bài này được ko ạ :(( Mình cảm ơn rất nhiều ạ
https://chat.lazi.vn/upload/images/2019/12/file_wgj1575206120.jpg
Toán lớp 8 nha
GIải hộ mình bài 4 câu a nhé <3
jhuyk;gggp-tg7
Có bạn nào biết làm bài này thì giúp mình nha mình đang cần gấp trước 2 giờ( rất gấp rồi chỉ còn 1 tiếng) mình cảm ơn nhiều (KO dùng hình bình hành, đường cao, tam giác cân, đường trung tuyến hay các kiến thức lớp 8) .Làm ơn hãy trả lời nhanh

tam giác ABM và tam giác KBM có
BK=BA
BM là cạnh chung
BM là phân giác góc B = > góc ABM = góc KBM
=> tam giác ABM = tam giác KBM ( c.g.c)
Đúng 0
Bình luận (2)
b: Ta có: ΔABM=ΔKBM
nên \(\widehat{BAM}=\widehat{BKM}=90^0\)
Xét ΔAME vuông tại A và ΔKMC vuông tại K có
MA=MK
\(\widehat{AME}=\widehat{KMC}\)
Do đó: ΔAME=ΔKMC
Suy ra: ME=MC
Đúng 1
Bình luận (1)
\(a,\left\{{}\begin{matrix}\widehat{ABM}=\widehat{KBM}\left(t/c.phân.giác\right)\\AB=BK\left(gt\right)\\BM.chung\end{matrix}\right.\Rightarrow\Delta ABM=\Delta KBM\left(c.g.c\right)\\ b,\Delta ABM=\Delta KBM\Rightarrow\left\{{}\begin{matrix}\widehat{MAB}=\widehat{MKB}=90^0\\MA=MK\end{matrix}\right.\\ \left\{{}\begin{matrix}\widehat{MAE}=\widehat{MKC}\left(=90^0\right)\\MA=MK\\\widehat{AME}=\widehat{KMC}\left(đối.đỉnh\right)\end{matrix}\right.\Rightarrow\Delta AME=\Delta KMC\left(cgv-gn\right)\\ \Rightarrow ME=MC\)
\(c,\Delta BEC\) có CA là đường cao \(\left(CA\perp BE\right)\), EK là đường cao \(\left(EK\perp BC\right)\), EK cắt CA tại M nên M là trực tâm
Do đó BM là đường cao thứ 3
Mà \(M\in BI\) nên BI là đường cao thứ 3 của tam giác BEC
\(\Rightarrow BI\perp EC\)
\(d,\) Vì \(AB=BK\) nên tam giác ABK cân tại B
\(\Rightarrow\widehat{BAK}=\dfrac{180^0-\widehat{ABK}}{2}\left(1\right)\)
Ta có \(\left\{{}\begin{matrix}AB=BK\\AE=CK\end{matrix}\right.\Rightarrow AB+AE=BK+KC\Rightarrow BE=BC\)
Do đó tam giác BEC cân tại B
\(\Rightarrow\widehat{BEC}=\dfrac{180^0-\widehat{ABK}}{2}\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow\widehat{BAK}=\widehat{BEC}\)
Mà 2 góc này ở vị trí đồng vị nên \(AK//EC\)
\(\Rightarrow AK\perp BI\left(EC\perp BI\right)\) hay \(AK\perp MQ\left(Q\in BI;M\in BI\right)\)
Xét tam giác AQK có KH là đường cao \(\left(KH\perp AQ\right)\), QM là đường cao \(\left(AK\perp QM\right)\) và KH cắt QM tại M nên M là trực tâm
Do đó AM là đường cao thứ 3 hay \(AM\perp QK\)
Mà \(AM\perp PK\left(gt\right)\)
Nên PK trùng QK hay 3 điểm K,P,Q thẳng hàng
Đúng 1
Bình luận (1)



