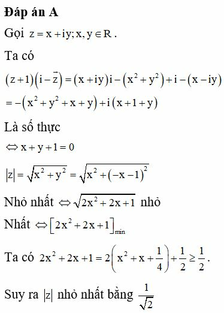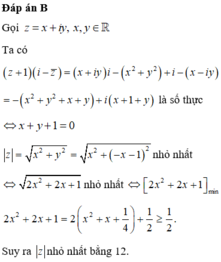Số giá trị của x thỏa mãn:Ix2+1I=5 là......
TL
Những câu hỏi liên quan
số giá trị của x thỏa mãn 2015Ix-1I+(x-1)=2016Ix-1I
tuổi con HN là :
50 : ( 1 + 4 ) = 10 ( tuổi )
tuổi bố HN là :
50 - 10 = 40 ( tuổi )
hiệu của hai bố con ko thay đổi nên hiệu vẫn là 30 tuổi
ta có sơ đồ : bố : |----|----|----|
con : |----| hiệu 30 tuổi
tuổi con khi đó là :
30 : ( 3 - 1 ) = 15 ( tuổi )
số năm mà bố gấp 3 tuổi con là :
15 - 10 = 5 ( năm )
ĐS : 5 năm
mình nha
Đúng 0
Bình luận (0)
Số giá trị của x thỏa mãn: (x2 + 1) + Ix - 1I + Ix3 + 1I = 0 là:
giá trị của x <0 thỏa mãn :Ix^2+1I=5
tao giai luon
Ix^2I=5-1
Ix^2I=4
=>X.2=4
x=4/2
x=2
nếu x<0 thì x=-2
Đúng 0
Bình luận (0)
Tập hợp các giá trị của x thỏa mãn Ix + 1I + I1 - xI = 2 là {........}
x = {3, 4 , 4,6,7,8,9,10,.....}
li-ke mình nhé
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn điều kiện
z
+
1
i
-
z
¯
là số thực. Khi đó môđun của z có giá trị nhỏ nhất bằng
Đọc tiếp
Cho số phức z thỏa mãn điều kiện z + 1 i - z ¯ là số thực. Khi đó môđun của z có giá trị nhỏ nhất bằng
![]()
![]()
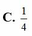
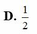
Cho số phức z thỏa mãn điều kiện
z
+
1
i
-
z
¯
là số thực. Khi đó môđun của z có giá trị nhỏ nhất bằng
Đọc tiếp
Cho số phức z thỏa mãn điều kiện z + 1 i - z ¯ là số thực. Khi đó môđun của z có giá trị nhỏ nhất bằng
![]()
![]()
![]()
![]()
Đáp án A
Gọi z = x + i y , x , y ∈ ℝ
z - 1 - i = 1 ⇔ x + i y - 1 - i = 1
⇔ x - 1 2 + y - 1 2 = 1 2 C
Gọi I là tâm của đường tròn (C).
Với mọi điểm P bất kì chạy trên S,
ta có O P ≤ O M + M P
do đó số phức tương ứng với P có môđun lớn nhất
khi và chỉ khi OP lớn nhất
OP = OM + MP
Tương đương 3 điểm O, M, P thẳng hàng
và M nằm giữa O và P
⇔ P ≡ P ' x P > 1
Phương trình đường thẳng OI: y = x
Tọa độ P’ là nghiệm của hệ phương trình :

Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn điều kiện
z
+
1
i
−
z
¯
là số thực. Khi đó môđun của z có giá trị nhỏ nhất bằng A.
1
4
B.
1
2
C.
1
2
D. 1
Đọc tiếp
Cho số phức z thỏa mãn điều kiện z + 1 i − z ¯ là số thực. Khi đó môđun của z có giá trị nhỏ nhất bằng
A. 1 4
B. 1 2
C. 1 2
D. 1
tính:C=\(\dfrac{5}{1.2}+\dfrac{5}{2.3}+\dfrac{5}{3.4}+...+\dfrac{5}{99.100}\)
tìm x: Ix+1I=5
Tìm các giá trị nguyên của n để phân số A= \(\dfrac{2n+5}{n+3}\)có giá trị là số nguyên
1)C=5/1.2+5/2.3+5/3.4+...+5/99.100
C=5.(1/1.2+1/2.3+1/3.4+...+1/99.100)
C=5.(1/1-1/2+1/2-1/3+1/3-1/4+...+1/99-1/100)
C=5.(1/1-1/100)
C=5.99/100
C=99/20
2)|x+1|=5
⇒x+1=5 hoặc x+1=-5
x=4 hoặc x=-6
Đúng 0
Bình luận (0)
3) Giải:
Để A=2n+5/n+3 là số nguyên thì 2n+5 ⋮ n+3
2n+5 ⋮ n+3
⇒2n+6-1 ⋮ n+3
⇒1 ⋮ n+3
Ta có bảng:
n+3=-1 ➜n=-4
n+3=1 ➜n=-2
Vậy n ∈ {-4;-2}
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn
z
1
m
2
+
2
m
,
trong đó m là số thực dương tùy ý. Biết rằng với mỗi m, tập hợp các điểm biểu diễn số phức
w
2
i
+
1
i
+
z
¯...
Đọc tiếp
Cho số phức z thỏa mãn z = 1 m 2 + 2 m , trong đó m là số thực dương tùy ý. Biết rằng với mỗi m, tập hợp các điểm biểu diễn số phức w = 2 i + 1 i + z ¯ − 5 + 3 i là một đường tròn bán kính r. Tìm giá trị nhỏ nhất của r
A. 3 2
B. 2 3
C. 3 5
D. 5 3
Đáp án C
Ta có:
w = 2 i + 1 i + z ¯ − 5 + 3 i = 2 i 2 + i + 2 i + 1 z ¯ − 5 + 3 i = − 7 + 4 i + 2 i + 1 z ¯ ⇔ w + 7 − 4 i = 2 i + 1 z ¯ ⇔ w + 7 − 4 i = 2 i + 1 z ¯ ⇔ w + 7 − 4 i = 5 z ¯ = 5 z = 5 1 m 2 + 2 m
theo bất đẳng thức AM-GM, ta có:
1 m 2 + 2 m = 1 m 2 + m + m ≥ 3 1 m 2 . m . m 3 = 3 ⇒ r min = 3 5
Đúng 0
Bình luận (0)