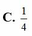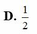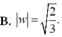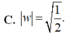Đáp án A
Gọi z = x + i y , x , y ∈ ℝ
z - 1 - i = 1 ⇔ x + i y - 1 - i = 1
⇔ x - 1 2 + y - 1 2 = 1 2 C
Gọi I là tâm của đường tròn (C).
Với mọi điểm P bất kì chạy trên S,
ta có O P ≤ O M + M P
do đó số phức tương ứng với P có môđun lớn nhất
khi và chỉ khi OP lớn nhất
OP = OM + MP
Tương đương 3 điểm O, M, P thẳng hàng
và M nằm giữa O và P
⇔ P ≡ P ' x P > 1
Phương trình đường thẳng OI: y = x
Tọa độ P’ là nghiệm của hệ phương trình :