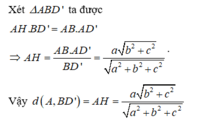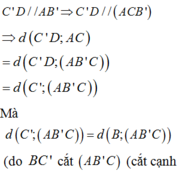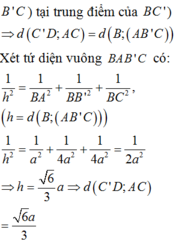cho hình hộp chữ nhật ABCD.A'B'C'D' , AB=AA'=2can2 . Khoảng cách từ A đến (BCD')
LL
Những câu hỏi liên quan
Cho hình hộp chữ nhật ABCD.ABCD có AB a, AD b, AA c. Tính khoảng cách từ điểm A đến đường thẳng BD
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AD = b, AA' = c. Tính khoảng cách từ điểm A đến đường thẳng BD'
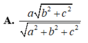

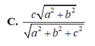
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
có
A
B
2
a
,
A
D
a
,
A
A
a
3
. Gọi M là trung điểm cạnh AB. Khoảng cách từ D đến mặt phẳng (BMC) bằn...
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = 2 a , A D = a , A A ' = a 3 . Gọi M là trung điểm cạnh AB. Khoảng cách từ D đến mặt phẳng (B'MC) bằng
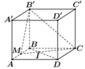
A. a 21 7
B. 2 a 21 7
C. 3 a 21 7
D. a 21 14
Khoảng cách từ D đến (B'MC)
gấp hai lần khoảng cách từ B đến (B'MC)
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = AB = a, AD = 2a. Tính khoảng cách h từ A tới mặt phẳng (B’D’C)
A. h = a
B. h = 2 a 3
C. h = 3 a 2
D. h = 4 a 3
Cho hình hộp chữ nhật ABCD.ABCD có AB AA 2a, AD a. Tính khoảng cách h từ C tới mặt phẳng (ABD) A. h
2
a
3
B. h
a
3
C. h
4
a
6
D. h
3
a
4
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D có AB = AA' = 2a, AD = a. Tính khoảng cách h từ C' tới mặt phẳng (A'BD)
A. h = 2 a 3
B. h = a 3
C. h = 4 a 6
D. h = 3 a 4
Hình hộp chữ nhật ABCD.A'B'C'D' có AB=a, BC=2a, AA'=a. Lấy điểm M trên cạnh AD sao cho AM=3MD
1, tính khoảng cách từ B đến mp ACB'
2, tính khoảng cách từ M đến mp AB'C
ta có :
\(V_{M.AB'C}=V_{B'.MAC}=\frac{B'B.S_{ABC}}{3}\)
Mà BB'=A'A=a
\(S_{AMC}=\frac{CD.AM}{2}=\frac{a.2a}{2.3}=\frac{a^2}{3}\)
=> \(V_{M.AB'C}=\frac{a^3}{9}\) (1)
=> dM,(AB'C)=\(\frac{3.V_{M.AB'C}}{S_{AB'C}}\) (2)
tam giác AB'C cps \(AB=B'C=2\sqrt{3}\)
và \(AB=a\sqrt{2}\)
=>\(S_{AB'C}=\frac{a^2\sqrt{5}}{2}\) (3)
Từ (1), (2)&(3)
=> dM;(AB'C)=\(\frac{2a}{3\sqrt{a}}\)
Đúng 0
Bình luận (1)
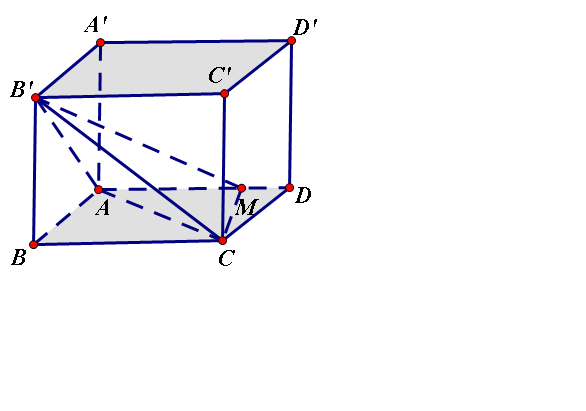
Pytago tính đuợc 3 cạnh
, \(MC=\frac{a\sqrt{5}}{2}\)
Dùng công thức Heron =>\(S_{AMC}=\frac{3a^2}{4}\)
\(V_{M.AB'C}=V_{B.AB'C}=\frac{a^3}{4}\)
Mặt khác dùng công thức Heron cũng tính được \(S_{AB'C}=\frac{3a^2}{2}\)
=> \(d_{\left(M;\left(AB'C\right)\right)}=\frac{3V_{M.AB'C}}{S_{AB'C}}=\frac{a}{2}\)
Đúng 0
Bình luận (1)
Cho hình hộp chữ nhật ABCDABCD có AB AD a, AA a
2
. Tính khoảng cách h từ D xuống mặt phẳng (BCD). A. h
a
2
3
B. h
a
2
3
C. h
a
3
D. h
a
2
Đọc tiếp
Cho hình hộp chữ nhật ABCDA'B'C'D' có AB = AD = a, AA' = a 2 . Tính khoảng cách h từ D xuống mặt phẳng (BCD').
A. h = a 2 3
B. h = a 2 3
C. h = a 3
D. h = a 2
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
có
A
B
A
A
a
,
A
D
a
3
. Khoảng cách giữa BD và CD’ bằng A.
a
7
B. 2a C.
a
3
7
D....
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = A A ' = a , A D = a 3 . Khoảng cách giữa BD và CD’ bằng
A. a 7
B. 2a
C. a 3 7
D. a 3 5
Đáp án C
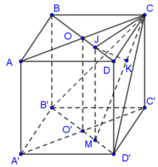
Kẻ CM vuông góc với B’D’; MJ vuông góc với BD; JK vuông góc với CM. Chứng minh khoảng cách giữa BD và CD’ bằng độ dài đoạn JK.
Thật vậy, ta có
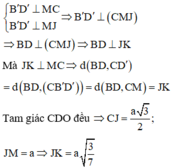
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
có
A
B
a
;
A
D
A
A
2
a
. Khoảng cách giữa hai đường thẳng AC và
D
C
bằng: A.
6
a
3...
Đọc tiếp
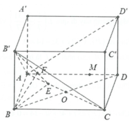
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = a ; A D = A A ' = 2 a . Khoảng cách giữa hai đường thẳng AC và D C ' bằng:
A. 6 a 3
B. 3 a 2
C. 3 a 3
D. 3 a 2
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
có
A
B
a
,
A
D
2
a
,
A
A
a
. Gọi M là điểm trên đoạn AD với
A
M
M
D...
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = a , A D = 2 a , A A ' = a . Gọi M là điểm trên đoạn AD với A M M D = 3 . Gọi x là độ dài khoảng cách giữa hai đường thẳng A'D, B'C và y là độ dài khoảng cách từ M đến mặt phẳng (AB'C). Tính giá trị xy.
A. 5 a 2 3
B. a 2 2
C. 3 a 2 4
D. 3 a 2 2