Hình bình hành ABCD có góc C<90 độ. Chứng minh rằng: \(AD^2=CD^2-CA^2-2CD.CD.cos\widehat{ACD}\)
H24
Những câu hỏi liên quan
câu 10 cho hình bình hành ABCD (AB//GÓC D=130\(^0\)
CD và góc B - góc C =50\(^0\)hãy tính các góc còn lại của hình thang
câu 11 cho hình bình hành ABCD có góc A =3 lần góc B.Hãy tính số đo góc của hình bình hành
Câu 10:
góc A=180-130=50 độ
góc B=(180+50)/2=230/2=115 độ
góc C=180-115=65 độ
Đúng 1
Bình luận (0)
Đúng ghi Đ, sai ghi SHình bình hành ABCD (hình bên) cóa, AB vuông góc với DCb, AH vuông góc với DCc, Chu vi hình bình hành ABCD là 18 cmd, Diện tích hình bình hành ABCD là 18
c
m
2
Đọc tiếp
Đúng ghi Đ, sai ghi S
Hình bình hành ABCD (hình bên) có
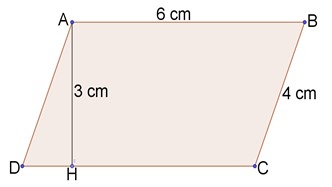
a, AB vuông góc với DC
b, AH vuông góc với DC
c, Chu vi hình bình hành ABCD là 18 cm
d, Diện tích hình bình hành ABCD là 18 c m 2
Hình bình hành ABCD có AC vuông góc với AD và AD=1/2 DC. Tính các góc của hình bình hành ABCD
Xét Δ vuông ADC ta có :
\(AD=\dfrac{CD}{2}\)
mà AD là cạnh góc vuông, CD là cạnh huyền
⇒ Δ ADC là tam giác nửa đều
\(\Rightarrow\left\{{}\begin{matrix}\widehat{ADC}=60^O\\\widehat{DCA}=30^O\end{matrix}\right.\)
\(\Rightarrow\widehat{ADC}=\widehat{ABC}=60^O\) (hai góc đối hình bình hành) (1)
Ta lại có : \(\widehat{BAC}=\widehat{DCA}\) (so le trong)
mà \(\widehat{DCA}=30^O\)
\(\Rightarrow\widehat{BAC}=30^2\)
mà \(\widehat{DAB}=\widehat{DAC}+\widehat{BAC}\)
\(\Rightarrow\widehat{DAB}=90^o+30^o=120^o\)
\(\Rightarrow\widehat{BCD}=\widehat{DAB}=120^o\) (hai góc đối hình bình hành) (2)
(1), (2)⇒ điều phải tính toán theo đề
Đúng 2
Bình luận (0)
Câu 39. Nếu hình bình hành ABCD có góc A 530 thìA.Góc D 530 B. Góc B Góc C 530. C. Góc C 1270 D. Góc D 1270 Câu 40. Hai cạnh kề của hình bình hành tỉ lệ với 1 và 2 và chu vi của hình bình hành bằng 30cm. Khi đó độ dài hai cạnh kề của hình bình hành làA. 12cm và 18cm B. 5cm và 10cm C. 15cm và 30cm D. 9cm và 18cm
Đọc tiếp
Câu 39. Nếu hình bình hành ABCD có góc A = 530 thì
A.Góc D= 530 B. Góc B= Góc C = 530.
C. Góc C= 1270 D. Góc D= 1270
Câu 40. Hai cạnh kề của hình bình hành tỉ lệ với 1 và 2 và chu vi của hình bình hành bằng 30cm. Khi đó độ dài hai cạnh kề của hình bình hành là
A. 12cm và 18cm B. 5cm và 10cm
C. 15cm và 30cm D. 9cm và 18cm
Xem thêm câu trả lời
Cho hình bình hành ABCD có góc A = 3 góc D Số đo góc C hình của hình thành là
Ta có: \(\widehat{A}+\widehat{D}=180^o\Rightarrow4\widehat{D}=180^o\Rightarrow\widehat{D}=45^o\)
Ta có:\(\widehat{C}+\widehat{D}=180^o\Rightarrow\widehat{C}=135^o\)
Đúng 3
Bình luận (0)
Cho hình bình hành ABCD có góc a = 3 góc B . Tính số đo các góc của hình bình hành
\(\widehat{A}=\widehat{C}=135^0\)
\(\widehat{B}=\widehat{D}=45^0\)
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có góc A = góc C và góc B = góc D
Chứng minh tứ giác ABCD là hình bình hành
Cho hình bình hành ABCD có phân giác góc D,góc B lần lượt cắt AB,DC tại E,F . C/m AD=AE , tứ giác EBFD là hình bình hành
Ta có: \(\widehat{DEA}=\widehat{EDC}\)(hai góc so le trong, AE//DC)
mà \(\widehat{EDC}=\widehat{ADE}\)(DE là tia phân giác của \(\widehat{ADC}\))
nên \(\widehat{ADE}=\widehat{AED}\)
Xét ΔAED có \(\widehat{ADE}=\widehat{AED}\)(cmt)
nên ΔAED cân tại A(Định lí đảo của tam giác cân)
Suy ra: AD=AE(đpcm)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có AB<CD.Phân giác góc A cắt BC tại I,phân giác góc C cắt Ad tại K. CMR AICK là hình bình hành
Đã là hình bình hành mà 2 cặp cạnh đối AB lại nhỏ hơn CD. Sai đề
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có BD vuông góc với BC. Biết AB=a, góc A = α . Tính diện tích hình bình hành ABCD theo a và α






