Cho hình vẽ:
Tìm \(\)anpha để Ax//By
Cho đoạn thẳng A, B . Trên cùng 1 nữa mặt phẳng bờ A, B. Vẽ các tia Ax và By trong đó góc bAx = anpha , góc ABy = 4 anpha. Tính anpha để cho Ax song song với By
Cho đoạn AB trên cùng nửa mặt phẳng bờ AB vẽ tia Ax và By trong đó BAx là góc anpha và BAy là 4 anph. Tính anpha để Ax song song By
Cho đoạn thẳng AB. Trên 1 nửa mặt phẳng bờ AB, vẽ các tia Ax và By trong đó góc BAx = anpha, góc ABy = 4 anpha. Tính anpha để cho Ax // By?
Mấy cậu giúp mình nha! Ai nhanh nhất mình tick cho:)
Cho hình vẽ, chứng minh: Ax song song By ( Ax//By )
Lời giải:
Ta thấy:
$\widehat{yBA}+\widehat{BAx}=124^0+56^0=180^0$. Mà 2 góc này ở vị trí trong cùng phía nên $By\parallel Ax$ (đpcm)
Cho hình vẽ:
a, Chứng tỏ rằng Ax // By b, Chứng minh By // Cz

a) Vẽ tia By' là tia đối của tia By
Ta có:
∠ABy' + ∠ABy = 180⁰ (kề bù)
⇒ ∠ABy' = 180⁰ - ∠ABy
= 180⁰ - 135⁰
= 45⁰
⇒ ∠ABy' = ∠BAx = 45⁰
Mà ∠ABy' và ∠BAx là hai góc so le trong
⇒ By // Ax
b) Ta có:
∠CBy' = ∠ABC - ∠ABy'
= 75⁰ - 45⁰
= 30⁰
⇒ ∠CBy' = ∠BCz = 30⁰
Mà ∠CBy' và ∠BCz là hai góc so le trong
⇒ By // Cz
bn có ghi sai đề bài ko đó , tui thấy nó hơi sai sai
Ax lm sao // vs By được chỉ vuông góc thôi??
a) Cho hình vẽ, biết Ax //By ,goc A= 30độ,gócAOB= 70 độ. Tính góc B
b) Cho hình vẽ, biết Góc A= 60 độ,góc B= 40 độ. tính số đo x,y
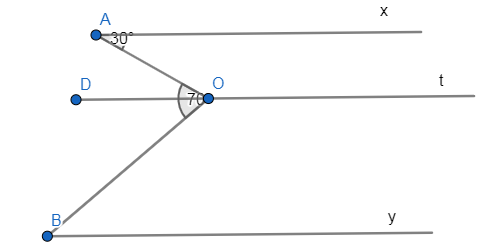
a, Kẻ Ot sao cho Ot song song với Ax và By, ta có:
\(\widehat{xAO}=\widehat{AOD}\) (So le trong)
\(\Rightarrow\widehat{xAO}=\widehat{AOD}=30^0\\\Rightarrow\widehat{DOB}=70^0-30^0=40^0\)
Mà OD//By
\(\Rightarrow\widehat{B}=\widehat{DOB}=40^0\)
Cho đường thẳng AB. Trên cùng một nửa mặt phẳng bờ AB vẽ tia Ax và By sao cho BAC = 2ABy= 42o. Tìm x để Ax // By.
vui lòng vẽ hình kèm theo
Bai 3:Cho hình vẽ dưới đây. Chứmg minh:
a) Ax // By
b) By // Cz
\(a,\widehat{xAB}+\widehat{xAt}=180^0\left(kề.bù\right)\\ \Rightarrow\widehat{xAB}=180^0-60^0=120^0\\ \Rightarrow\widehat{xAB}=\widehat{yBA}\left(=120^0\right)\)
Mà 2 góc này ở vị trí so le trong nên \(Ax//By\)
\(b,\widehat{yBC}+\widehat{ABC}+\widehat{yBA}=360^0\\ \Rightarrow\widehat{yBC}=360^0-120^0-90^0=150^0\\ \Rightarrow\widehat{yBC}=\widehat{BCz}\left(=150^0\right)\)
Mà 2 góc này ở vị trí so le trong nên \(By//Cz\)