Làm thế nào để phân tích đa thức thành nhân tử cho phương trình bậc 2 cách dễ hiểu nhất
TN
Những câu hỏi liên quan
cho mình hỏi làm thế nào để phân tích đa thức thành nhân tử bậc bốn có nghiệm nguyên mà không dùng máy tính?
vì là nghiệm nguyên nên bạn chỉ cần nhẩm nghiệm xong dùng lược đồ hóc ne là được bạn nhé
lược đồ hóc ne là gì vậy bạn
Các bạn ơi! Giảng cho mình hiểu bài phân chia đa thức thành nhân tử bằng cách phối nhiều phương pháp cái phần tách hay thêm, bớt hạng tử. Bạn nào giảng dễ hiểu mình tích cho, mình đã nói là làm. Mình đang cần gấp lắm ngày mai là học rồi mà vẫn đọc hông hiểu gì. :( ...... làm ơn nha....♥♥♥♥♥♥
Sau khi lướt quanh mục Toán lớp 8 anh thấy có khá nhiều cách phân tích đa thức bậc 4 thành nhân tử (toàn mấy cách hai năm trước anh chưa học không à): từ đưa về bình phương tổng 3 hạng tử, bấm máy tìm nghiệm, đồng nhất hệ số... Vậy bạn nào giúp mình phân tích đa thức này thành nhân tử đi. Anh làm thử mà không ra:
\(x^4-6x^3+9x^2-3x+12\)
Gửi Thắng Nguyễn: Mình không biết tại sao lại ko phân tích được?
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Phân tích đa thức sau thành nhân tử tổng hợp
x^3 + x^2 + 4
Làm từng bước và giải thích tại sao làm vậy cho mk dễ hiểu nhen
Do trình đọ thấp nên ko thể thông hiểu nhanh được
\(x^3+x^2+4=x^3+2x^2-x^2+2x-2x+4\)
\(=x^2\left(x+2\right)-x\left(x+2\right)-2\left(x+2\right)\)
\(=\left(x^2-x-2\right)\left(x+2\right)\)
\(=\left(x^2-2x+x-2\right)\left(x+2\right)\)
\(=\left\{x\left(x-2\right)+\left(x-2\right)\right\}\left(x+2\right)\)
\(=\left(x+1\right)\left(x-2\right)\left(x+2\right)\)
Đúng 0
Bình luận (0)
Nhưng tại sao làm bước phân tích đầu tiên đấy
Đúng 0
Bình luận (0)
Mình chỉ cho bạn chỗ sai của Thanh Ngân này.
\(x^3+x^2+4=x^3+2x^2-x^2-2x+2x+4\)
\(=x^2\left(x+2\right)-x\left(x+2\right)+2\left(x+2\right)\)
\(=\left(x^2-x+2\right)\left(x+2\right)\)
Bước đầu là tìm nghiệm. Nghiệm của đa thức phải là nghiệm của hạng tử tự do. Như trong đa thức trên, nghiệm của đa thức phải là nghiệm của 4 và bạn thử các nghiệm thấy x=-2 thỏa mãn thì phải có thừa số x+2 khi phân tích thành nhân tử.
Mong bạn hiêu lời giải. Chúc bạn học tốt.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Phân tích các đa thức sau thành nhân tử bằng cách dùng hằng đẳng thức a) (3x + 1)^2 - 4(x - 2)^2b) (a^2 + b^2 - 5)^2 - 4(ab +2)^2 Phân tích các đa thức sau thành nhân tử bằng phương pháp tách một hạng tử thành nhiều hạng tử a) 3x^2 + 9x - 30 b) x^3 - 5x^2 - 14x Làm nhớ từng bước cho dễ hiểu....Làm đúng tick sau 30 giây làm bài
Đọc tiếp
Phân tích các đa thức sau thành nhân tử bằng cách dùng hằng đẳng thức
a) (3x + 1)^2 - 4(x - 2)^2
b) (a^2 + b^2 - 5)^2 - 4(ab +2)^2
Phân tích các đa thức sau thành nhân tử bằng phương pháp tách một hạng tử thành nhiều hạng tử
a) 3x^2 + 9x - 30
b) x^3 - 5x^2 - 14x
Làm nhớ từng bước cho dễ hiểu....
Làm đúng tick sau 30 giây làm bài
1.a) (3x+1)2-4(x-2)2= (3x+1)2-[2(x-2)]2=[(3x+1)-2(x-2)][(3x+1)+2(x-2)]=(x+3)(5x-1)
b) (a2+b2-5)2-4(ab+2)2= (a2+b2-5)2-[2(ab+2)]2 = (a2+b2-5-2ab-4)(a2+b2-5+2ab+4)=[(a-b)2-9][(a+b)2-1]
2. 3x2+9x-30=3x2-6x+15x-30=3x(x-2)+15(x-2)=3(x+5)(x-2)
b. x3-5x2-14x=x3+2x2-7x2-14x=x2(x+2)-7x(x+2)=(x2-7x)(x+2)
Đúng 0
Bình luận (0)
a) \(\left(3x+1\right)^2-4\left(x-2\right)^2\)
\(=\left(3x+1\right)^2-\left[2.\left(x-2\right)\right]^2\)
\(=\left(3x+1\right)^2-\left(2x-4\right)^2\)
\(=\left[3x+1-2x+4\right].\left[3x+1+2x-4\right]\)
\(=\left(x+5\right)\left(5x-3\right)\)
b) \(\left(a^2+b^2-5\right)^2-4\left(ab+2\right)^2\)
\(=\left(a^2+b^2-5\right)^2-\left[2.\left(ab+2\right)\right]^2\)
\(=\left(a^2+b^2-5\right)^2-\left(2ab+4\right)^2\)
\(=\left(a^2+b^2-5-2ab-4\right)\left(a^2+b^2-5+2ab+4\right)\)
\(=\left[\left(a-b\right)^2-9\right].\left[\left(a+b\right)^2-1\right]\)
\(=\left[\left(a-b-3\right)\left(a-b+3\right)\right].\left[\left(a+b-1\right)\left(a+b+1\right)\right]\)
a) \(3x^2+9x-30\)
\(=3\left(x^2+3x-10\right)\)
\(=3\left(x^2-2x+5x-10\right)\)
\(=3.\left[x\left(x-2\right)+5.\left(x-2\right)\right]\)
\(=3.\left[\left(x+5\right)\left(x-2\right)\right]\)
b) \(x^3-5x^2-14x\)
\(=x\left(x^2-5x-14\right)\)
\(=x\left(x^2+2x-7x-14\right)\)
\(=x.\left[x\left(x+2\right)-7.\left(x+2\right)\right]\)
\(=x.\left[\left(x-7\right)\left(x+2\right)\right]\)
Đúng 0
Bình luận (0)
Cho xin mẹo: cách phân tích đa thức thành nhân tử bằng phương pháp tách 1 hạng tử thành nhiều hạng tử đối với các đa thức có bậc ba trở lên
phương pháp này mình gọi là phương pháp nhẩm nghiệm:
- Nếu tổng tất cả các hệ số bằng o thì đa thức có 1 nghiệm là x=1 hay chứa thừa số là x-1
- Nếu tổng tất cả các hệ số bậc chẵn bằng tổng các hệ số bậc lẻ thì đa thức có một nghiệm là x=-1 hay chứa thừa số là x+1
Đúng 0
Bình luận (0)
Khi phân tích đa thức x2 + 4x – 2xy – 4y + y2 thành nhân tử, bạn Việt làm như sau: x2 + 4x – 2xy – 4y + y2 (x2 - 2xy + y2) + (4x – 4y) (x - y)2 + 4(x – y) (x – y)(x – y + 4). Em hãy chỉ rõ trong cách làm trên, bạn Việt đã sử dụng những phương pháp nào để phân tích đa thức thành nhân tử.
Đọc tiếp
Khi phân tích đa thức x2 + 4x – 2xy – 4y + y2 thành nhân tử, bạn Việt làm như sau:
x2 + 4x – 2xy – 4y + y2 = (x2 - 2xy + y2) + (4x – 4y)
= (x - y)2 + 4(x – y)
= (x – y)(x – y + 4).
Em hãy chỉ rõ trong cách làm trên, bạn Việt đã sử dụng những phương pháp nào để phân tích đa thức thành nhân tử.
x2 + 4x – 2xy – 4y + y2 = (x2-2xy+ y2) + (4x – 4y) → bạn Việt dùng phương pháp nhóm hạng tử
= (x - y)2 + 4(x – y) → bạn Việt dùng phương pháp dùng hằng đẳng thức và đặt nhân tử chung
= (x – y)(x – y + 4) → bạn Việt dùng phương pháp đặt nhân tử chung
Đúng 0
Bình luận (0)
cho em hỏi,có cách nào để nhẩm được nghiệm của pt bậc cao nhằm áp dụng hoocne phân tích đa thức thành nhân tử nhanh ko ạ?
\(\Sigma\) các hệ số =0 ta có 1 nghiệm là x=1
\(\Sigma\) hệ số chẵn =\(\Sigma\) hệ số lẻ ta có 1 nghiệm là x= -1
vd \(4x^5-4x^4-21x^3+19x^2+20x-12=0\)
ta có
tổng hệ số chẳn là : \(-4+19-12=3\)
tổng hệ số lẻ là :\(4-21+20=3\)
vậy pt trên có 1 nghiệm là -1 từ đó bạn dùng hoocno đẻ phân tích nha
\(\Sigma\)
Đúng 0
Bình luận (2)
Cho em hỏi tí ạ, mong các bạn và thầy cô giúp đỡ ạ.Bài này phần b phân tích đa thức thành nhân tử em còn chưa hiểu chỗ phân tích như thế nào để từ x^2-5x+1 thành ^{ }
Đọc tiếp
Cho em hỏi tí ạ, mong các bạn và thầy cô giúp đỡ ạ.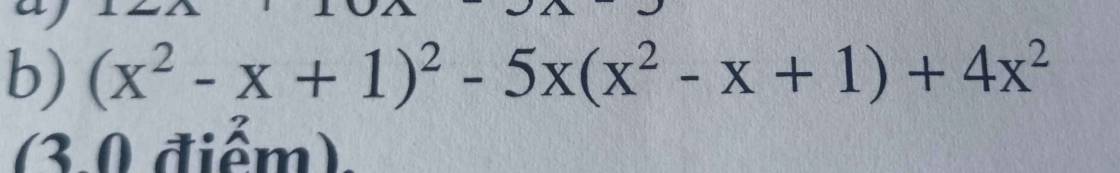
Bài này phần b phân tích đa thức thành nhân tử em còn chưa hiểu chỗ phân tích như thế nào để từ x^2-5x+1 thành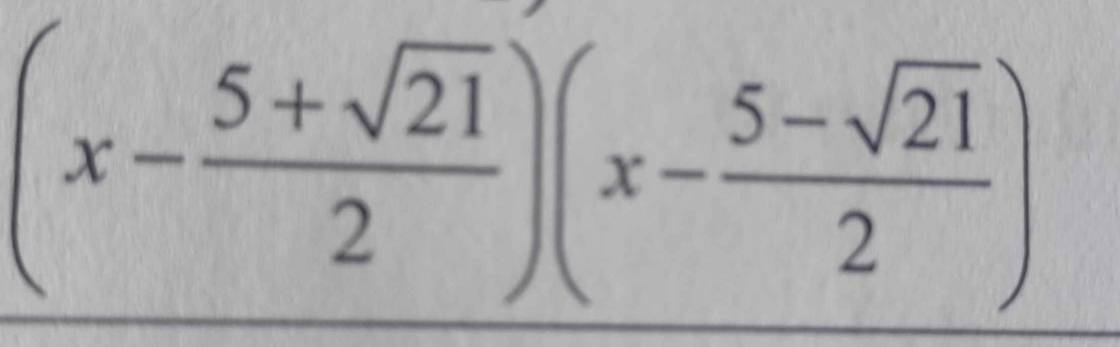
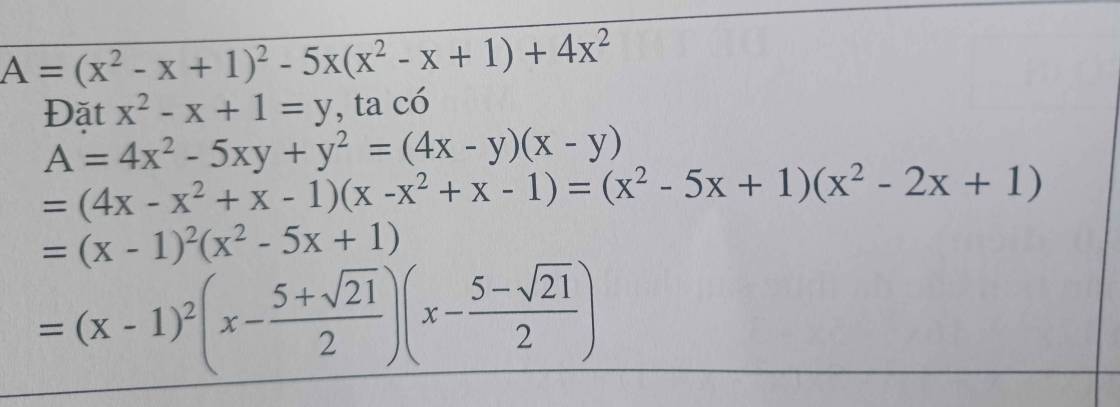 \(\) \(^{ }\)
\(\) \(^{ }\)
Giải thích: `x^2-5x+1`
`=x^2-2. 5/2x+25/4-21/4`
`=(x-5/2)^2-21/4`
`=(x-5/2-\sqrt{21}/2)(x-5/2+\sqrt{21}/2)`
`=(x-[5+\sqrt{21}]/2)(x-[5-\sqrt{21}]/2)`
Đúng 6
Bình luận (0)



