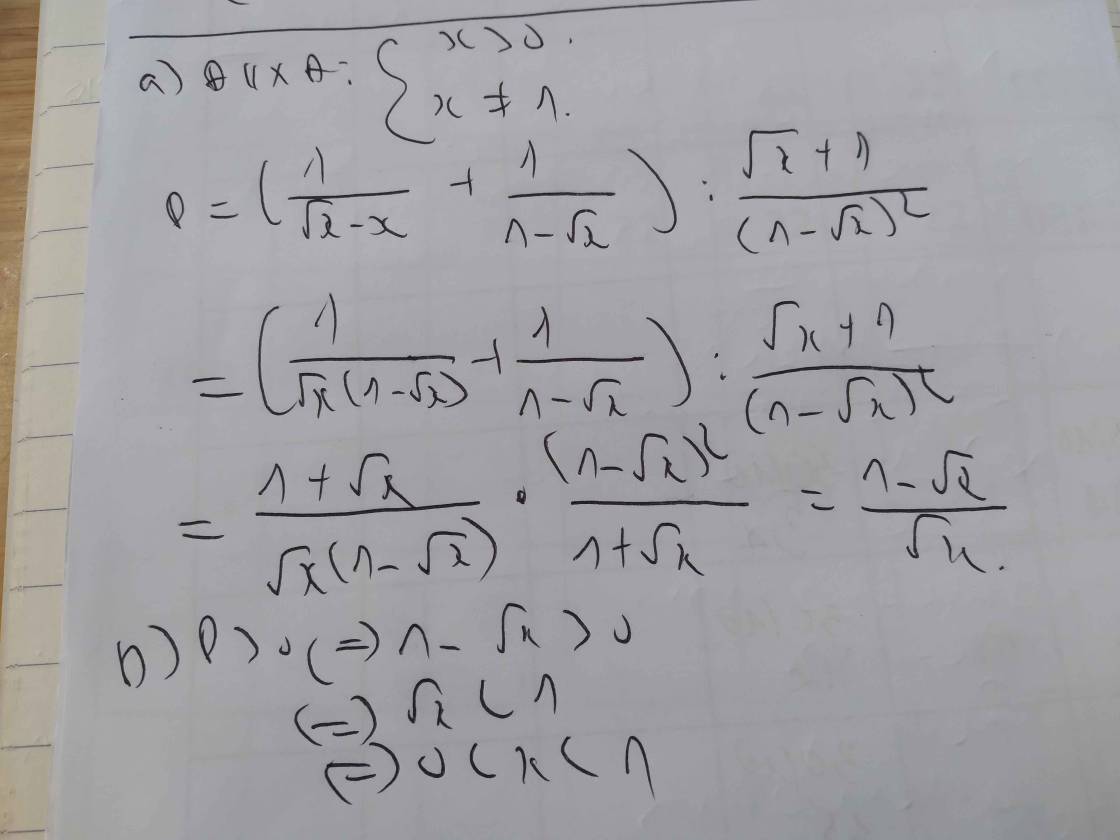P= \(\dfrac{x+9}{6\sqrt{x}}\) đk x>0; x khác 4. Tìm GTNN của P
H24
Những câu hỏi liên quan
Rút gọn (Giải chi tiết từng bước với ạ)
\(A=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{x-9}\) (ĐK: x≥0;x≠9)
Với x ≥ 0; x ≠ 9 ta có:
\(A=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{x-9}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x-3}\right)+2\sqrt{x}\left(\sqrt{x}+3\right)-3x-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{x-3\sqrt{x}+2x+6\sqrt{x}-3x-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{3\sqrt{x}-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{3\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{3}{\sqrt{x}+3}\)
Vậy \(A=\dfrac{3}{\sqrt{x}+3}\).
Đúng 1
Bình luận (1)
Cho biểu thức A = \(\dfrac{\sqrt{x}-2}{\sqrt{x}}\) và B = \(\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{2x}{x-9}\) Đk: x>0, x≠9
a, Rút gọn B
b, Đặt P = A.B. Tìm giá trị nguyên nhỏ nhất của x để |P| > P.
a: \(B=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-2x}{x-9}=\dfrac{x-3\sqrt{x}}{x-9}=\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
b: \(P=A\cdot B=\dfrac{\sqrt{x}-2}{\sqrt{x}}\cdot\dfrac{\sqrt{x}}{\sqrt{x}+3}=\dfrac{\sqrt{x}-2}{\sqrt{x}+3}\)
Để |P|>P thì P<0
=>căn x-2<0
=>0<x<4
=>x=1
Đúng 0
Bình luận (0)
Tìm ĐK để căn thức xác định:
a) \(\sqrt{x-9}+\sqrt{6-x}\)
b) \(\sqrt{\dfrac{-1}{x^2}}\)
a. không có ĐK, vì muốn a đc xác định cần \(\sqrt{x-9}\) và \(\sqrt{6-x}\) \(\ge0\)
mà điều kiện để \(\sqrt{x-9}\) và \(\sqrt{6-x}\ge0\) là \(9\le x\le6\)
Dễ thấy không có số nào tương thích với x
Đúng 1
Bình luận (0)
Rút gọn:
a, A frac{sqrt{x}}{sqrt{x}-6}-frac{3}{sqrt{x}+6}+frac{x}{36-x} (đk: x ≥ 0 và x ≠ 36)
b, B frac{9-x}{sqrt{x}+3}-frac{x-6sqrt{x}+9}{sqrt{x}-3}-6 (đk: x ≥ 0 và x ≠ 9)
c, C frac{a+b}{left(sqrt{a}-sqrt{b}right)^2}-frac{2}{sqrt{ab}}:left(frac{1}{sqrt{a}}-frac{1}{sqrt{b}}right)^2 (đk: a 0, b 0 và a ≠ b)
d, D left(frac{2-asqrt{a}}{2-sqrt{a}}+sqrt{a}right)left(frac{2-sqrt{a}}{2-a}right) (đk: a ≥ 0, a ≠ 2, a ≠ 4)
Đọc tiếp
Rút gọn:
a, A = \(\frac{\sqrt{x}}{\sqrt{x}-6}-\frac{3}{\sqrt{x}+6}+\frac{x}{36-x}\) (đk: x ≥ 0 và x ≠ 36)
b, B = \(\frac{9-x}{\sqrt{x}+3}-\frac{x-6\sqrt{x}+9}{\sqrt{x}-3}-6\) (đk: x ≥ 0 và x ≠ 9)
c, C = \(\frac{a+b}{\left(\sqrt{a}-\sqrt{b}\right)^2}-\frac{2}{\sqrt{ab}}:\left(\frac{1}{\sqrt{a}}-\frac{1}{\sqrt{b}}\right)^2\) (đk: a > 0, b > 0 và a ≠ b)
d, D = \(\left(\frac{2-a\sqrt{a}}{2-\sqrt{a}}+\sqrt{a}\right)\left(\frac{2-\sqrt{a}}{2-a}\right)\) (đk: a ≥ 0, a ≠ 2, a ≠ 4)
\(B=\frac{9-x}{\sqrt{x}+3}-\frac{x-6\sqrt{x}+9}{\sqrt{x}-3}-6\)(đk: x ≥ 0 và x ≠ 9)
\(B=\frac{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}{\sqrt{x}+3}-\frac{\left(\sqrt{x}-3\right)^2}{\sqrt{x}-3}-6\)
\(B=\left(3-\sqrt{x}\right)-\left(\sqrt{x}-3\right)-6\)
\(B=3-\sqrt{x}-\sqrt{x}+3-6\)
\(B=-2\sqrt{x}\)
Đúng 0
Bình luận (0)
\(A=\frac{\sqrt{x}}{\sqrt{x}-6}-\frac{3}{\sqrt{x}+6}+\frac{x}{36-x}\)(đk: x ≥ 0 và x ≠ 36)
\(=\frac{\sqrt{x}}{\sqrt{x}-6}-\frac{3}{\sqrt{x}+6}-\frac{x}{x-36}\)
\(=\frac{\sqrt{x}}{\sqrt{x}-6}-\frac{3}{\sqrt{x}+6}-\frac{x}{x-36}\)
\(=\frac{\sqrt{x}\left(\sqrt{x}+6\right)-3\left(\sqrt{x-6}\right)-x}{(\sqrt{x}-6)\left(\sqrt{x}+6\right)}\)
\(=\frac{x+6\sqrt{x}-3\sqrt{x}+18-x}{(\sqrt{x}-6)\left(\sqrt{x}+6\right)}\)
\(=\frac{3\sqrt{x}+18}{(\sqrt{x}-6)\left(\sqrt{x}+6\right)}\)
\(=\frac{3(\sqrt{x}+6)}{(\sqrt{x}-6)\left(\sqrt{x}+6\right)}\)
\(=\frac{3}{\sqrt{x}-6}\)
Đúng 0
Bình luận (0)
Cho A= \(\dfrac{\sqrt{x}+4}{{}\sqrt{x}-1}\) và B= \(\dfrac{x+2\sqrt{x}}{\sqrt{x}(\sqrt{x}+1)} -\dfrac{3\sqrt{x}-3}{x-1}\) (đk: x>0,x≠1)
a) Rút gọn P=A.B
b) Tìm x để P(\(\sqrt{x}+1\)) ≤ 6-x
c) Tìm x để P nhận giá trị nguyên
Cho \(^{\dfrac{x\sqrt{x}-1}{x+\sqrt{x}+1}+\dfrac{x-1}{\sqrt{x}-1}}\) ( Đk x ≥ 0,x≠1)
giải
\(=\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{x+\sqrt{x}+1}+\sqrt{x}+1=\sqrt{x}-1+\sqrt{x}+1=2\sqrt{x}\)
Đúng 0
Bình luận (1)
A=\(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\) và \(B=\dfrac{\sqrt{x}-2}{\sqrt{x}}\) đk : x> 0; x khác 4
Cho P = A.B
Tìm GTNN của P
Ta có: \(P=A\cdot B\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\cdot\dfrac{\sqrt{x}-2}{\sqrt{x}}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
Đúng 1
Bình luận (0)
cho biểu thức
P=\(\left(\dfrac{1}{\sqrt{x}-x}+\dfrac{1}{1-\sqrt{x}}\right)\):\(\dfrac{\sqrt{x}+1}{\left(1-\sqrt{x}\right)^2}\)
a) tìm đk và rút gọn
b) Tìm x để P>0
Cho biểu thức: \(A\) = \(\left(\dfrac{3+\sqrt{x}}{3-\sqrt{x}}-\dfrac{3-\sqrt{x}}{3+\sqrt{x}}-\dfrac{4x}{x-9}\right)\) : \(\left(\dfrac{5}{3-\sqrt{x}}-\dfrac{4\sqrt{x}+2}{3\sqrt{x}-x}\right)\) . Tìm đk của x để |A| > - A
ĐKXĐ: x>0; x<>9
\(A=\left(\dfrac{-\left(\sqrt{x}+3\right)}{\sqrt{x}-3}+\dfrac{\sqrt{x}-3}{\sqrt{x}+3}-\dfrac{4x}{x-9}\right):\left(\dfrac{5\sqrt{x}-4\sqrt{x}-2}{\sqrt{x}\left(3-\sqrt{x}\right)}\right)\)
\(=\dfrac{-x-6\sqrt{x}-9+x-6\sqrt{x}+9-4x}{x-9}:\dfrac{-\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{-4x-12\sqrt{x}}{x-9}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{-\left(\sqrt{x}-2\right)}\)
\(=\dfrac{4x\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}{\left(x-9\right)\left(\sqrt{x}-2\right)}=\dfrac{4x}{\sqrt{x}-2}\)
|A|>-A
=>A>=0
=>4x>0
=>x>0 và x<>9
Đúng 0
Bình luận (0)