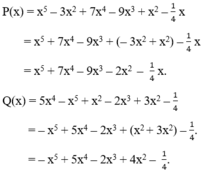x2 - 14
LT
Những câu hỏi liên quan
x2- 14/260 - 14/416 - ... - 14/19400 = 1/25
x2- 14/260 - 14/416 - ... - 14/19400 = 1/25
e/ 94 x2 – 25y2
f/ x2 - xy + 14 y2
\(\dfrac{9}{4}x^2-25y^2=\left(\dfrac{3}{2}x-5y\right)\left(\dfrac{3}{2}x+5y\right)\)
\(x^2-xy+\dfrac{1}{4}y^2=\left(x-\dfrac{1}{2}y\right)^2\)
Đúng 0
Bình luận (0)
Tìm các giới hạn sau:
lim
x
→
0
x
2
+
1
-
1
4
-
...
Đọc tiếp
Tìm các giới hạn sau: lim x → 0 x 2 + 1 - 1 4 - x 2 + 16
lim x → 0 x 2 + 1 - 1 4 - x 2 + 16 = 4
Đúng 0
Bình luận (0)
a(3x4-x2+1):(x-4)
b(x4-x2-13x-14):(x2-3x-7)
c(x3-2x2-10x-7):(x2-7-3x)
giúp mik với
a: \(=\dfrac{3x^4-12x^3+12x^3-48x^2+47x^2-168x+168x-672+673}{x-4}\)
\(=3x^3+12x^2+47x+168+\dfrac{673}{x-4}\)
b: \(=\dfrac{x^4-3x^3-7x^2+3x^3-9x^2-21x+15x^2-45x-105+53x+91}{x^2-3x-7}\)
\(=x^2+3x+15+\dfrac{53x+91}{x^2-3x-7}\)
c: \(=\dfrac{x^3-3x^2-7x+x^2-3x-7}{x^2-3x-7}=x+1\)
Đúng 2
Bình luận (0)
Tập nghiệm của phương trình
x
−
x
2
−
1
4
+
x
+
x
2
−
1
2
là: A.
∅
B.
7...
Đọc tiếp
Tập nghiệm của phương trình x − x 2 − 1 4 + x + x 2 − 1 = 2 là:
A. ∅
B. 7 2 ; 1
C. 0
D. 1
Đặt t = x − x 2 − 1 4 , t > 0
x − x 2 − 1 4 = t ⇒ t 2 = x − x 2 − 1 = x − x 2 − 1 x + x 2 − 1 x + x 2 − 1
x 2 − x 2 + 1 x + x 2 − 1 = 1 x + x 2 − 1 = 1 x + x 2 − 1 ⇒ x + x 2 − 1 = 1 t 2
Ta có pt: t + 1 t 2 = 2 ⇔ t 3 − 2 t 2 + 1 = 0 ⇔ t = 1 t = 1 + 5 2 t = 1 − 5 2
So sánh với điều kiện t > 0 ta tìm được t = 1 , t = 1 + 5 2
Trường hợp 1: t = 1 : x − x 2 − 1 4 = 1 ⇔ x − x 2 − 1 = 1
⇔ x − 1 = x 2 − 1 ⇔ x ≥ 1 x 2 − 2 x + 1 = x 2 − 1 ⇔ x = 1
Trường hợp 2: t = 1 + 5 2 ⇒ x − x 2 − 1 4 = 1 + 5 2
⇔ x − x 2 − 1 = 7 + 3 5 2 ⇔ x − 7 + 3 5 2 = x 2 − 1
⇔ x ≥ 7 + 3 5 2 x − 7 + 3 5 2 2 = x 2 − 1 ⇔ x ≥ 7 + 3 5 2 x = 7 2 ⇒ x ∈ ∅
Kết hợp hai trường hợp ta được nghiệm x = 1
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Bài 1: Tìm các số x; y; z biết rằng:
a) và xyz = 810; b) và x2 + y2 + z2 = 14.
b) và x2 + y2 + z2 = 14.
Cho hai đa thức:
P
x
x
5
-
3
x
2
+
7
x
4
-
9
x
3
+
x
2
-
1
4
Q
x
5
x
4
-
x...
Đọc tiếp
Cho hai đa thức:
P x = x 5 - 3 x 2 + 7 x 4 - 9 x 3 + x 2 - 1 4
Q x = 5 x 4 - x 5 + x 2 - 2 x 3 + 3 x 2 - 1 4
Sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm của biến
Đơn giản biểu thức:a)
x
+
1
2
x
2
−
1
2
x
+
1
4
;
b) (x – 3y)(
x
2
+ 3xy + 9...
Đọc tiếp
Đơn giản biểu thức:
a) x + 1 2 x 2 − 1 2 x + 1 4 ; b) (x – 3y)( x 2 + 3xy + 9 y 2 );
c) ( x 2 – 3)( x 4 + 3 x 2 + 9); d) (2x – 1)(4 x 2 + 2x + 1).
a) x 2 - 1 4 b) x 2 - 9 y 2
c) x 4 - 9 d) 4 x 2 - 1
Đúng 0
Bình luận (0)