cho hình vẽ hãy chứng minh: a) Ax // Ot ; b) By//Ot
DL
Những câu hỏi liên quan
cho hình vẽ hãy chứng minh: a) Ax // Ot ; b) By//Ot
Cho hình vẽ bên, biết
O
A
x
^
30°,
O
B
y
^
150° và Ot là tia phân giác của
A
O
B
^
60°. Chứng minh ba đường thẳng Ax, By và Ot đôi một song song
Đọc tiếp
Cho hình vẽ bên, biết O A x ^ = 30°, O B y ^ = 150° và Ot là tia phân giác của A O B ^ = 60°. Chứng minh ba đường thẳng Ax, By và Ot đôi một song song
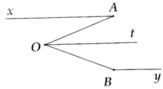
Vì Ot là phân giác A O B ^ nên:
= A O t ^ = B O t ^ = 1 2 A O B ^ = 1 2 . 60° = 30°
=> x A O ^ = A O t ^ => Ax // Ot (1)
Lại có : t O A ^ + O B y ^ = 30° +150° = 180° => Ot // By. (2)
Từ (1) và (2), ta có Ax // By // Ot
Đúng 0
Bình luận (0)
Cho hình vẽ bên, biết
O
A
x
^
30
°
,
O
B
y
^
150
°
và Ot là tia phân giác của
A
O
B
^
60
°
. Chứng minh ba đường thẳng Ax, By và Ot đôi một song song.
Đọc tiếp
Cho hình vẽ bên, biết O A x ^ = 30 ° , O B y ^ = 150 ° và Ot là tia phân giác của A O B ^ = 60 ° . Chứng minh ba đường thẳng Ax, By và Ot đôi một song song.
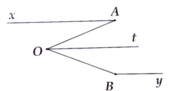
Ở hình vẽ bên cho biết OAx=35°, OBy=140°, AOB=75°. Qua O, kẻ tia Ot nằm giữa hai tia OA và OB sao cho Ot // Ax. Chứng minh:
a) Ot // By
b) Ax // By.
cho hình vẽ hãy chứng minh AB // CD (hướng dẫn vẽ Ot // AB ) góc A = 135, góc B = 120, góc C = 105
MIK KO BT VẼ HÌNH CÓ AI BT BÀI NÀY CHỈ MIK VỚI
1) cho góc xOy khác góc bẹt , Ot là tia phân giác của góc đó . trên tia Ot lấy điểm H , qua H vẽ đường thẳng vuông góc vs Ot cắt Ox tại A , Oy tại B
a) chứng minh : tam giác AHO = tam giác BHO
b) trên tia Ax lấy điểm C , trên tiaBy lấy D sao cho AC =BD . chứng minh AD = BC
c) chứng minh AB // CD
Bài 35 sgk toán 7 phải k lý lệ anh hồng
Đúng 0
Bình luận (0)
Cho góc xOy nhọn, Ot là tia phân giác của góc xOy. Trên tia Ot lấy H. Qua H vẽ đường thẳng vuông góc với Ot cắt Ox tại A, Oy tại B.
a/ Chứng minh tam giác AHO = tam giác BHO.
b/ Trên tia Ax lấy C, trên tia By lấy D sao cho AC = BD. Chứng minh AD = BC.
c/ CD cắt tia Ot tại K. Chứng minh AB // CD.
Help me, please!!!!!!!
Ta có hình vẽ:
a) Vì Ot là phân giác của góc xOy nên \(xOt=yOt=\frac{xOy}{2}\)
Xét Δ AHO và Δ BHO có:
AOH = BOH (cmt)
OH là cạnh chung
AHO = BHO = 90o
Do đó, Δ AHO = Δ BHO (g.c.g) (đpcm)
b) Δ AHO = Δ BHO (câu a)
=> OA = OB (2 cạnh tương ứng)
Gọi K' là giao điểm của AD và BC
Xét Δ AOK' và Δ BOK' có:
OA = OB (cmt)
AOK' = BOK' ( câu a)
OK' là cạnh chung
Do đó, Δ AOK' = Δ BOK' (c.g.c)
=> AK' = BK' (2 cạnh tương ứng); OAK' = OBK' (2 góc tương ứng)
Lại có: OAK' + K'AC = 180o (kề bù) (1)
OBK' + K'BD = 180o (kề bù) (2)
Từ (1) và (2) => K'AC = K'BD
Xét Δ K'AC và Δ K'BD có:
AC = BD (gt)
K'AC = K'BD (cmt)
AK' = BK' (cmt)
Do đó, Δ K'AC = Δ K'BD (c.g.c)
=> K'C = K'D (2 cạnh tương ứng)
Mà AK' = BK' (cmt) => AK' + K'D = BK' + K'C
=> AD = BC (đpcm)
c) Đầu tiên ta đi chứng minh 3 điểm O, H, K' thẳng hàng (bn tự chứng minh)
Δ AOK' = BOK' (câu b)
=> AK'O = BK'O (2 góc tương ứng) (*)
Δ K'AC = Δ K'BD (câu b)
=> AK'C = BK'D (2 góc tương ứng) (**)
Ta có: AK'O + AK'C + CK'K = 180o
BK'O + BK'D + DK'K = 180o
Kết hợp với (*) và (**) => CK'K = DK'K
Δ OK'C và Δ OK'D có:
OK' là cạnh chung
COK' = DOK' (câu a)
OC = OD (vì OA = OB; AC = BD)
Do đó, Δ OK'C = Δ OK'D (c.g.c)
=> K'C = K'D (2 cạnh tương ứng)
Xét Δ CK'K và Δ DK'K có:
CK' = DK' (cmt)
CK'K = DK'K (cmt)
K'K là cạnh chung
Do đó, Δ CK'K = Δ DK'K (c.g.c)
=> CKK' = DKK' (2 góc tương ứng)
Mà CKK' + DKK' = 180o (kề bù) nên CKK' = DKK' = 90o
=> \(KK'\perp CD\)
Mà \(KK'\perp AB\) do \(Ot\perp AB\) nên AB // CD (đpcm)
Đúng 1
Bình luận (3)
thẳng AB cắt Ot tại M. Chứng minh a) OAM = OBM; b) AM = BM; OM AB c) OM là đường trung trực của AB d) Trên tia Ot lấy điểm N . Chứng minh NA = NB Bài 2. Cho ABC vuông tại A, trên tia đối của tia CA lấy điểm K sao cho CK = CA, từ K kẻ KE vuông góc với đường thẳng AC. Chứng mỉnhằng: a) AB // KE b) ABC = KEC ; BC = CE Bài 3. Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C. Trên tia Oy lấy hai điểm B,D sao cho OA = OB, AC = BD. a) Chứng minh: AD = BC. b) Gọi E là giao điểm AD và BC. Chứng minh: EAC = EBD c) Chứng minh: OE là phân giác của góc xOy, OE CD Bài 4. Cho ABC coù BÂ=900, gọi M là trung điểm của BC. Trên tia đối của tia AM lấy điểm E sao cho ME = MA. a) Tính BCE b) Chứng minh BE // AC. Bài 5. Cho ABC, lấy điểm D thuộc cạnh BC ( D không trùng với B,C). Gọi Mlà trung điểm của AD. Trên tia đối của tia MB lấy điểm E sao cho ME= MB, trên tia đối của tia MC lấy điểm F sao cho MF= MC. Chứng minh rằng: a) AME = DMB; AE // BC b) Ba điểm E, A, F thẳng hàng c) BF // CE Bài 6: Cho có B = C , kẻ AH BC, H BC . Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh: a) AB = AC b) ABD = ACE c) ACD = ABE d) AH là tia phân giác của góc DAE e) Kẻ BK AD, CI AE. Chứng minh ba đường thẳng AH, BK, CI cùng đi qua một điểm
Đúng 0
Bình luận (5)
Cho tam giác ABC cân tại A, có Am là đường trung tuyến. Vẽ tia Ax // BC. Vẽ tia Cy // AM, Ax cắt Cy tại I
a/ Chứng minh AM vuông góc BC
b/ Chứng minh AC = MI
c/ Chứng minh ABMI là hình bình hành
Giúp e vs ạ!
không cần vẽ hình
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến ứng với cạnh đáy BC
nên AM là đường cao ứng với cạnh BC
b: Xét tứ giác AMCI có
AI//MC
AM//CI
Do đó: AMCI là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCI là hình chữ nhật
hay AC=MI
c: Ta có: AICM là hình chữ nhật
nên AI=MC
mà MB=MC
nên AI=MB
Xét tứ giác AIMB có
AI//MB
AI=MB
Do đó: AIMB là hình bình hành
Đúng 1
Bình luận (0)
Cho hình vẽ bên biết OAx= 30 độ , OBy=150 độ và Ot là tia phân giác của AOB=60 độ.
Chứng minh ba đường thẳng Ax, By và Ot đôi một song song.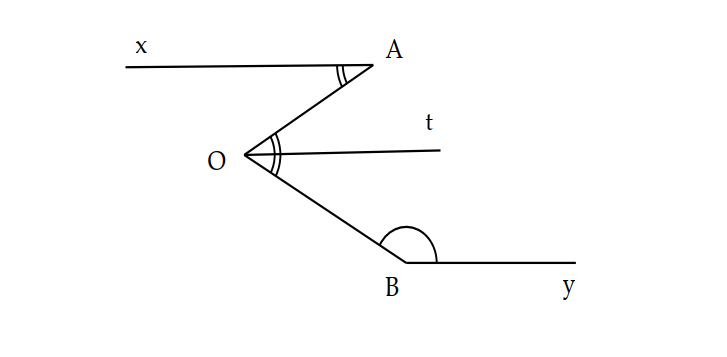
Ta có: \(\widehat{AOt}=\widehat{BOt}=\dfrac{\widehat{AOB}}{2}=60^0:2=30^0\)(do Ot là phân giác \(\widehat{AOB}\))
Ta có: \(\widehat{AOt}=\widehat{OAx}=30^0\)
Mà 2 góc này so le trong
=> Ax//Ot(1)
Ta có: \(\widehat{BOt}+\widehat{OBy}=30^0+150^0=180^0\)
Mà 2 góc này là 2 góc trong cùng phía
=> By//Ot(2)
Từ (1),(2) => đpcm
Đúng 3
Bình luận (0)
Cho góc xOy khác góc bẹt, Ot là tia phân giác của góc đó. Trên tia Ot lấy điểm H qua điểm H vẽ đường thẳng vuông góc với Ot, cắt Ox tại A, Oy tại B.
a) Chứng minh rằng ΔAHD= ΔBHD
b) Trên tia Ax lấy điểm C, trên tia By lấy điểm D sao cho AC=BD. Chứng minh AD=BC
c) CD cắt tia Ot tại K. Chứng minh AB//CD
Bạn có nhầm đề ko?? Trong hình ko có điểm D nào hết?!!




