Với số a bất kì, so sánh: a với a – 1

Với số a bất kì, so sánh: a với a + 2

cho m<n hãy so sánh

m+5, n+5

m-4,n-4

m-6,n+5

với số a bất kì hãy so sánh 

a+1,a+4

a-2,3+a

a^2-a+3>a+2

a^2+a-1 với a>,= 1

bài 1:với 2 số nguyên a,b cùng dấu dương,so sánh  a-1/a và b+1/b

bài 2:cho n là 1 số tự nhiên bất kì .cmr n+3 và 2n+5 là 2 số nguyên tố cùng nhau

bài 3:cho tổng S=1+3+5+...+2009+2011

CMR:n là 1 số chính phương

bài 4:cho A=2/3.4/5.6/7....4998/4999

Hãy so sánh A và 0,02

Cho 3 điểm A B C thẳng hàng , B nằm giữa A và C . Biết BA=2cm, BC=3cm. Lấy điểm H bất kì trên đường thẳng vuông góc với AC tại B 

Cho hình chữ nhật abcd. Trên cd lấy m bất kì, nối m với a và b. So sánh diện tích hình tam giác amb với tổng diện tích 2 hình tam giác adm và bmc ( không có số đo)

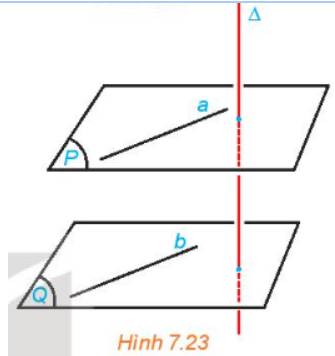
Cho hai mặt phẳng (P) và (Q) song song với nhau và đường thẳng \(\Delta \) vuông góc với (P). Gọi b là một đường thẳng bất kì thuộc (Q). Lấy một đường thẳng a thuộc (P) sao cho a song song với b (H.7.23). So sánh (\(\Delta \), b) và (\(\Delta \), a). Từ đó rút ra mối quan hệ giữa \(\Delta \) và (Q).

Cho AB = 6cm, C là điểm bất kì nằm giữa A và B.I là trung điểm AC, K là trung điểm BC.

a) Tính IK

b) So sánh AK với (AB + AC) :2

a. biểu diễn tập nghiệm của mãi bất phương trình sau trên trục số :

x ≥ - 1 ; x < 3

b. cho a < b , so sánh -3a + 1 với -3b +1