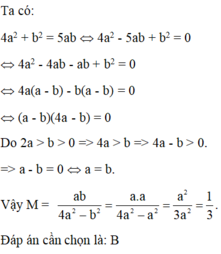Các số a, b thỏa mãn điều kiện là 4a2+b2= 5ab và 4a> b. Chứng minh rằng 2a>b>0
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
HA
Những câu hỏi liên quan
BÀI 1:
a) Chứng minh rằng : nếu 2a>b>0 thì 4a>b
b) Các số a ,b thỏa mãn điều kện 4a2+b2= 5ab
c) chứng minh rằng nếu 4a>b thì 2a>b>0
a \(2a>b;2a>0\Rightarrow2a+2a>b+0\Rightarrow4a>b\)
b \(4a^2+b^2=5ab\Rightarrow4a^2+b^2-5ab=0\Rightarrow\left(4a^2-4ab\right)-\left(ab-b^2\right)=0\)
\(\Rightarrow4a\left(a-b\right)-b\left(a-b\right)=0\Rightarrow\left(4a-b\right)\left(a-b\right)=0\Rightarrow\hept{\begin{cases}4a-b=0\Rightarrow4a=b\\a-b=0\Rightarrow a=b\end{cases}}\)
Đúng 0
Bình luận (0)
c \(20=4\cdot5>11\)mà \(2\cdot5=10>11\)đâu
sai đề r
Đúng 0
Bình luận (0)
cho 4a2 +b2 =5ab và 2a>b>0 . tính P = ab/4a2-b2
=>4a^2-5ab+b^2=0
=>(a-b)(4a-b)=0
=>a=b hoặc b=4a(loại)
=>P=b^2/3b^2=1/3
Đúng 1
Bình luận (0)
Cho các số thực a, b, c thỏa mãn điều kiện : (0 < c < b< a<=3); (2ab <= 2a+3b); (3abc <= ab+3bc+2ca.)
Chứng minh rằng a³ +b³ + c³<= 36.
Cho 4a2 + b2 5ab và 2a b 0. Tính giá trị của biểu thức:
M
ab
4a
2
−
b
2
A.
1
9
B.
1
3
C. 3 D. 9
Đọc tiếp
Cho 4a2 + b2 = 5ab và 2a > b > 0. Tính giá trị của biểu thức: M = ab 4a 2 − b 2
A. 1 9
B. 1 3
C. 3
D. 9
Chứng minh rằng nếu các số nguyên a,b thỏa mãn điều kiện 2a2+a=3b2+b thì a-b và 2a +2b+1 là các số chính phương.
Làm nhak mk tik cko
Các cao nhân giúp mình vớiBài 1: Cho n 3 và n ∈ N. Chứng minh nếu 2n 10a + b với a; b ∈ N và 0 b 9 thì ab ⋮ 6Bài 2: Cho các số nguyên dương thỏa mãn a2 + b2 c2. Chứng minh rằng abc ⋮ 60Bài 3: Chứng minh rằng nếu a + 1 và 2a + 1 đều là các số chính phương thì a ⋮ 24Bài 4: Chứng minh rằng nếu a + 1 và 3a + 1 đều là các số chính phương thì a ⋮ 40Bài 5: Cho 3 số nguyên dương thỏa mãn a3 + b3 + c3 ⋮ 14. Chứng minh rằng abc cũng ⋮ 14Bài 6: Cho biểu thức S n4 + 2n3 – 16n2 – 2n + 15. Tìm tất cả cá...
Đọc tiếp
Các cao nhân giúp mình với
Bài 1: Cho n > 3 và n ∈ N. Chứng minh nếu 2n = 10a + b với a; b ∈ N và 0 < b < 9 thì ab ⋮ 6
Bài 2: Cho các số nguyên dương thỏa mãn a2 + b2 = c2. Chứng minh rằng abc ⋮ 60
Bài 3: Chứng minh rằng nếu a + 1 và 2a + 1 đều là các số chính phương thì a ⋮ 24
Bài 4: Chứng minh rằng nếu a + 1 và 3a + 1 đều là các số chính phương thì a ⋮ 40
Bài 5: Cho 3 số nguyên dương thỏa mãn a3 + b3 + c3 ⋮ 14. Chứng minh rằng abc cũng ⋮ 14
Bài 6: Cho biểu thức S = n4 + 2n3 – 16n2 – 2n + 15. Tìm tất cả các giá trị nguyên của n để S ⋮ 16
Cho a, b, c là các số dương thỏa mãn điều kiện
1
a
+
1
b
+
1
c
≤
3
. Chứng minh rằng:
a
1
+
b
2
+
b
1
+
c
2
+
c...
Đọc tiếp
Cho a, b, c là các số dương thỏa mãn điều kiện 1 a + 1 b + 1 c ≤ 3 . Chứng minh rằng: a 1 + b 2 + b 1 + c 2 + c 1 + a 2 + 1 2 ( a b + b c + c a ) ≥ 3
Ta chứng minh BĐT
( a + b + c ) ( 1 a + 1 b + 1 c ) ≥ 9 ( * ) ( * ) < = > 3 + ( a b + b a ) + ( b c + c b ) + ( c a + a c ) ≥ 9
Áp dụng BĐT Cô – si cho hai số dương ta có:
a b + b a ≥ 2 b c + c b ≥ 2 c a + a c ≥ 2 =>(*) đúng
= > 9 a + b + c ≤ 1 a + 1 b + 1 c ≤ 3 = > a + b + c ≥ 3
Trở lại bài toán: Áp dụng BĐT Cô si cho hai số dương ta có 1 + b 2 ≥ 2 b
Ta có: a 1 + b 2 = a − a b 2 1 + b 2 ≥ a − a b 2 2 b = a − a b 2 ( 1 )
Tương tự ta có:
b 1 + c 2 ≥ b − b c 2 ( 2 ) c 1 + a 2 ≥ c − c a 2 ( 3 )
Cộng từng vế của (1), (2) và (3) ta có:
a 1 + b 2 + b 1 + c 2 + c 1 + a 2 ≥ a + b + c − 1 2 ( a b + b c + c a ) = > a 1 + b 2 + b 1 + c 2 + c 1 + a 2 + 1 2 ( a b + b c + c a ) ≥ a + b + c ≥ 3
Đúng 0
Bình luận (0)
Cho 4a2 + b2 = 5ab với b > 2a > 0. Tính giá trị của biểu thức 5ab / 3a^2+2b^2
Ta có:
\(4a^2+b^2=5ab\Leftrightarrow4a^2+b^2-4ab-ab=0\)
\(\Leftrightarrow4a\left(a-b\right)-b\left(a-b\right)=0\)
\(\Leftrightarrow\left(a-b\right)\left(4a-b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a-b=0\\4a-b=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=b\left(ktm\right)\\4a=b\left(tm\right)\end{matrix}\right.\)
\(\Rightarrow4a=b\)
\(\Rightarrow\dfrac{5ab}{3a^2+2b^2}=\dfrac{5a.4a}{3a^2+2.\left(4a\right)^2}=\dfrac{20a^2}{3a^2+32a^2}\)
\(=\dfrac{20a^2}{35a^2}=\dfrac{4}{7}\)
Đúng 0
Bình luận (0)
\(4a^2+b^2=5ab\)
\(\Rightarrow4a\left(a-b\right)-b\left(a-b\right)=0\)
\(\Rightarrow\left(a-b\right)\left(4a-b\right)=0\)
\(\Rightarrow b=4a\left(do.a\ne b\right)\)
\(\dfrac{5ab}{3a^2+2b^2}=\dfrac{20a^2}{3a^2+32a^2}=\dfrac{4}{7}\)
Đúng 0
Bình luận (0)
Cho a,b thuộc N thỏa mãn điều kiện 2a2+a=3b2+b
Chứng minh rằng a-b và 2a+2b+1 đều là số chính phương
Có bổ đề sau: \(a^2=pq\) với \(a,p,q\in Z^+\) và \(\left(p,q\right)=1\) thì p,q là hai số chính phương
\(2a^2-2b^2+a-b=b^2\Leftrightarrow\left(a-b\right)\left(2a+2b+1\right)=b^2\)(*)
Gọi d là UWCLN của a-b và 2a+2b+1 ta có từ (*) b chia hết d.
a-b chia hết cho d nên 2a-2b chia hết cho d . Vậy 2a+2b+1-(2a-2b) chia hết d
nên 4b+1 chia hết d mà b chia hết cho d nên 1 chia hết d. Vậy hai số a-b và 2a+2b+1 nguyên tố cùng nhau
Áp dụng bổ đề có đpcm
Đúng 0
Bình luận (0)