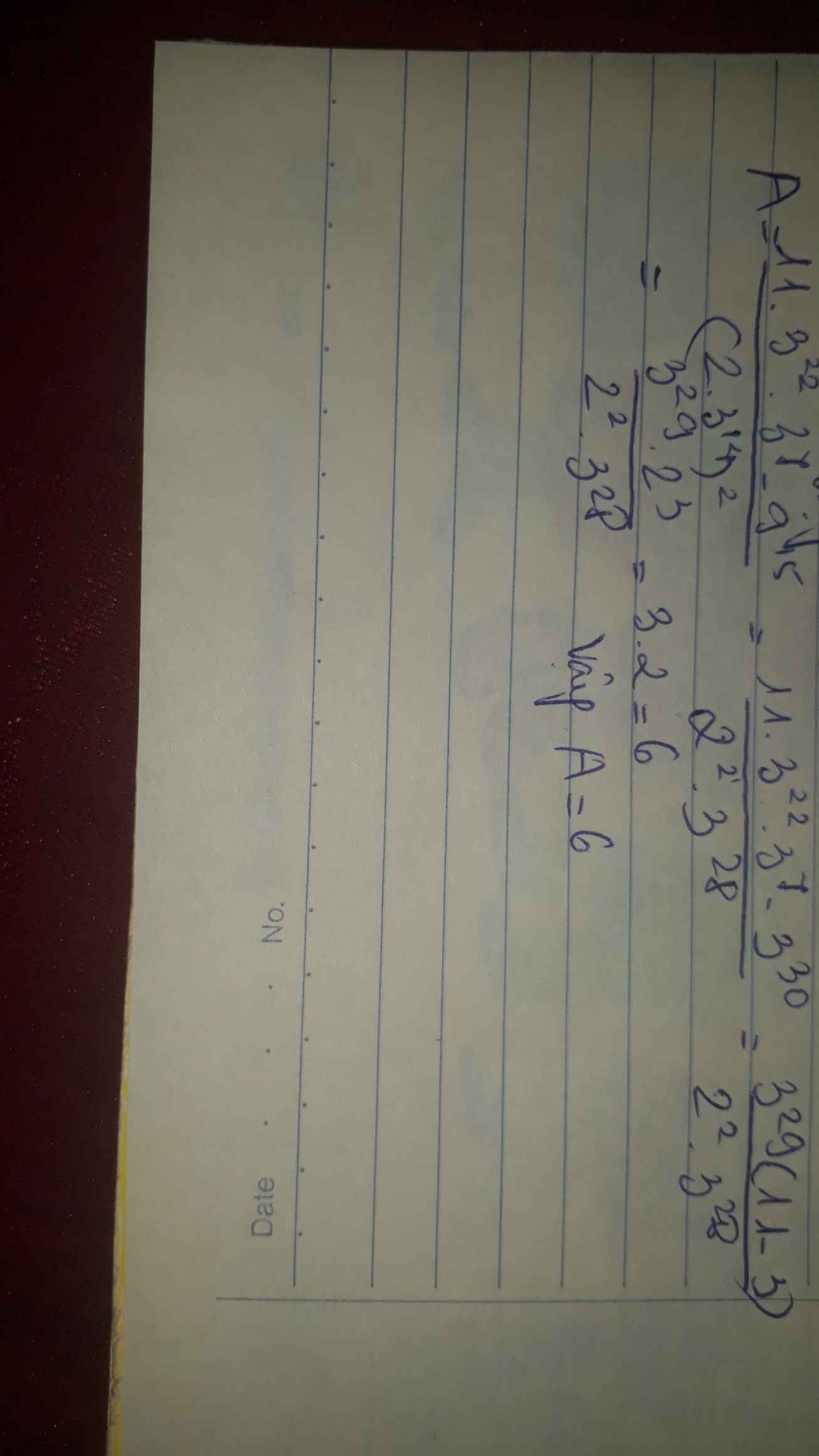\(A=\frac{11.3^{22}.3^7-9^{15}}{\left(2.3^{14}\right)^2}\)
DN
Những câu hỏi liên quan
A = \(\frac{11.3^{22}.3^7-9^{15}}{\left(2.3^{14}\right)^2}\)
Tính
A=\(\frac{11.3^{22}.3^7-9^{15}}{\left(2.3^{14}\right)^2}\)
Tính :
A = \(\dfrac{11.3^{22}.3^7-9^{15}}{\left(2.3^{14}\right)^2}\)
A=\(\dfrac{11.3^{22}.3^7-9^{15}}{\left(2.3^{14}\right)^2}=\dfrac{11.3^{29}-3^{29}.3}{2^2.3^{28}}=\dfrac{3^{29}.\left(11-3\right)}{2^2.3^{28}}=\dfrac{3^{29}.2^3}{2^2.3^{28}}=3.2=6\)
Đúng 1
Bình luận (0)
\(A=\dfrac{11\cdot3^{22}\cdot3^7-9^{15}}{\left(2\cdot3^{14}\right)^2}=\dfrac{11\cdot3^{29}-3^{30}}{2^2\cdot3^{28}}\)
\(=\dfrac{3^{29}\cdot2^3}{3^{28}\cdot2^2}=3\cdot2=6\)
Đúng 1
Bình luận (0)
\(\frac{11.3^{22}.3^7-9^{15}}{^{ }\left(2.3^{14}\right)^2}\)
\(\frac{11.3^{22}.3^7-9^{15}}{\left(2.3^{14}\right)^2}\)
\(\frac{11.3^{22}.3^7-9^{15}}{\left(2.3^{14}\right)^2}\)=?
Tính :
a ) \(\frac{11.3^{22}.3^7-9^{15}}{\left(2.3^{14}\right)^2}\)
b ) 27^16 : 9^10
a ) \(\frac{11\cdot3^{22}\cdot3^7-9^{15}}{\left(2\cdot3^{14}\right)^2}=\frac{11\cdot3^{29}-\left(3^2\right)^{15}}{2^2\cdot3^{28}}\)
\(=\frac{3^{28}\left(11\cdot3-3^2\right)}{2^2\cdot3^{28}}=\frac{33-9}{4}=\frac{24}{4}=6\)
b ) \(27^{16}\div9^{10}\)
\(=\left(3^3\right)^{16}\div\left(3^2\right)^{10}\)
\(=3^{48}\div3^{20}\)
\(=3^{48-20}\)
\(=3^{28}\)
Bg
a) \(\frac{11.3^{22}.3^7-9^{15}}{\left(2.3^{14}\right)^2}\)
= \(\frac{11.3^{22}.3^7-3^{30}}{2^2.3^{28}}\)
= \(\frac{11.3^{29}-3.3^{29}}{4.3^{28}}\)
= \(\frac{8.3^{29}}{4.3^{28}}\)
= \(\frac{2.3}{1.1}\)
= 6
b) 2716 ÷ 910
= 33.16 ÷ 32.10
= 348 ÷ 320
= 348 - 20
= 328
A = \(\frac{11.3^{22}.3^7-9^{15}}{\left(2.3^{14}\right)^2}\)
Giải đầy đủ ra mới tk nhé
\(A=\frac{11.3^{22+7}-\left(3^2\right)^{15}}{2^2.\left(3^{14}\right)^2}=\frac{11.3^{29}-3^{30}}{2^2.3^{28}}=\frac{3^{29}.\left(11-3\right)}{2^2.3^{28}}=\frac{3^{29}.2^3}{2^2.3^{28}}=\hept{\frac{3}{ }}\)\(=3.2=6\)
Đúng 0
Bình luận (0)
bạn bỏ phần \(=\hept{\begin{cases}3\\\end{cases}}\)mình ghi lộn
Đúng 0
Bình luận (0)
\(A=\frac{11.3^{22}.3^7-9}{\left(2.3^{14}\right)^2}\)
Xem thêm câu trả lời