a) Hãy nêu tính chất của trọng tâm của một tam giác; các cách xác định trọng tâm
b) Bạn Nam nói: "Có thể vẽ được một tam giác có trọng tâm ở bên ngoài tam giác". Bạn Nam nói đúng hay sai ? Tại sao ?
Hãy nêu tính chất trọng tâm của một tam giác; các cách xác định trọng tâm.
- Trọng tâm của một tam giác có tính chất như sau:
"Trọng tâm cách đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó."
- Các cách xác định trọng tâm:
+ Cách 1: Vẽ hai đường trung tuyến ứng với hai cạnh tùy ý, rồi xác định giao điểm của hai đường trung tuyến đó.
+ Cách 2: Vẽ một đường trung tuyến của tam giác. Chia độ dài đường trung tuyến thành ba phần bằng nhau rồi xác định một điểm cách đỉnh hai phần bằng nhau.
Hãy nêu tính chất của trọng tâm của một tam giác : các cách xác định trọng tâm.
là trọng tâm của một tam giác 3-2x 180 :3
Câu hỏi: a, hãy nêu tính chất của trọng tâm tam giác; các cách xác định trọng tâm
b, bạn Nam nói : "có thể vẽ đc một t/g có trọng tâm ở bên ngoài t/g". Bạn Nam nói đúng hay sai? TẠi sao
ai nhanh nhất và đúng mk sẽ tick cho
a, Trọng tâm của tam giác cách đỉnh 2/3 đường trung tuyến đi qua đỉnh ấy
Cánh xác định trọng tâm: vẽ 2 đường trung tuyến của tam giác, 2 đường đó cắt nhau tại điểm nào thì đó là trọng tâm của tam giác
b, Bạn Nam nói sai. Vì 3 đường trung tuyến của tam giác luôn ở trong tam giác nên giao điểm của chúng hay trọng tâm của tam giác luôn ở trong tam giác
Chết!!! Quên xuống dòng rồi! Chịu khó đọc nhé bạn ^^!
hãy nêu tính chất của trực tâm , trọng tâm
+) trực tâm của tam giác.
Tính chất: "Khoảng cách từ một đỉnh tới trực tâm của một tam giác bằng hai lần khoảng cách từ tâm đường tròn ngoại tiếp tam giác đó đến trung điểm cạnh nối hai đỉnh còn lại".
Chú ý: Trực tâm của tam giác vuông trùng với đỉnh của tam giác vuông đó.Tính chất:
Trong tam giác cân, đường trung trực của cạnh đáy đồng thời là đường trung tuyến, đường phân giác, đường cao xuất phát từ đỉnh đối diện của cạnh đó.
Trực tâm của tam giác nhọn ABC trùng với tâm đường tròn nội tiếp tam giác tạo bởi ba đỉnh là chân ba đường cao từ các đỉnh A,B,C đến các cạnh BC,AC,AB tương ứng.
+) trọng tâm của tam giác
Định lý: Ba đương trung tuyến của tam giác cùng đi qua điểm. điểm đó cách đỉnh một khoảng bằng
23 độ dài đường trung tuyến đi qua đỉnh ấy.
Các pn giúp mk chứng minh tính chất trọng tâm của tam giác nha.
Nghĩa là: cho tam giác ABC có G là trọng tâm tam giác . Chứng minh AG = 2/3 độ dài đường trung tuyến xuất phát từ đỉnh A của tam giác ABC.
Giúp mình tiếp nha :))) [ ENDGAME ]
6.
a) Hãy nêu tính chất của trọng tâm của một tam giác ; các cách xác định trọng tâm.
b) Bạn Nam nói : " Có thể vẽ được 1 tam giác có trọng tâm ở bên ngoài tam giác ". Bạn Nam nói đúng hay sai ? Tại sao ?
7.
- Những tam giác nào có ít nhất 1 đường trung tuyến đồng thời là đường phân giác , đường trung trực , đường cao ?
8.
- Những tam giác nào có trọng tâm đồng thời là trực tâm , điểm cách đều ba đỉnh , điểm ( nằm trong tam giác ) cách đều ba cạnh ???
Giúp mình nha , 3 bài cuối rồi :)))))
~Mino~
a) Tính chất trong SGK . Xác định thì đầy cách.
Cách 1 : Chứng minh là giao điểm 2 đường trung tuyến
Cách 2 : Gỉa sử AM là trung tuyến ,G thuộc AM Chứng minh \(GM=\frac{1}{3}AM\)thì là trọng tâm Hoặc tùy
Cách khác là cách nâng cao
Câu 7 :
Tam giác cân, tam giác đều
Câu 8:
Tam giác đều
b) Trung tuyến xuất phát từ đỉnh và đi qua trung điểm của cạnh đối diện.
3 trung tuyến cùng cắt nhau tại 1 điểm là trọng tâm
Vì vậy ko thể nào có trọng tâm nằm ngoài tam giác ( vìTrung tuyến xuất phát từ đỉnh và đi qua trung điểm của cạnh đối diện nó nằm ngoài thì gọi gì là trung tuyến nữa )
suy ra Nam sai
Trong tình huống mở đầu, người ta chứng minh được G chính là trọng tâm của tam giác ABC. Em hãy cắt một mảnh bìa hình tam giác. Xác định trọng tâm của tam giác và đặt mảnh bìa đó lên một giá nhọn tại trọng tâm vừa xác định. Quan sát xem mảnh bìa có thăng bằng không?
Cắt mảnh bìa hình tam giác. Kẻ 2 đường trung tuyến của tam giác ABC, chúng cắt nhau tại G.
Đặt mảnh bìa đó lên một giá nhọn tại trọng tâm G thì thấy mảnh bìa thăng bằng.
Biết rằng: Trong một tam giác vuông. Đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền. Hãy giải bài toán sau:
Cho tam giác vuông ABC có hai góc vuông AB = 3cm, AC= 4cm. Tính khoảng cách từ đỉnh A tới trọng tâm G của tam giác ABC.
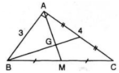
ΔABC vuông tại A có BC2 = AB2 + AC2 (định lí Pitago)
⇒ BC2 = 32 + 42 = 25 ⇒ BC = 5 (cm)
Gọi M là trung điểm của BC ⇒ AM là trung tuyến.
Vì theo đề bài: trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên
Cho tam giác ABC có H là trực tâm, H không trùng với đỉnh nào của tam giác. Nêu một tính chất của cặp đường thẳng:
a) AH và BC; b) BH và CA; c) CH và AB.
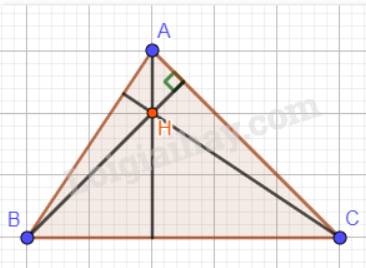
Tam giác ABC có H là trực tâm nên:
a) \(AH \bot BC\);
b) \(BH \bot AC\);
c) \(CH \bot AC\).