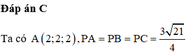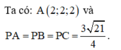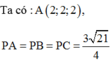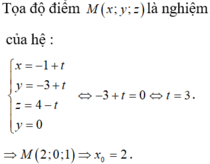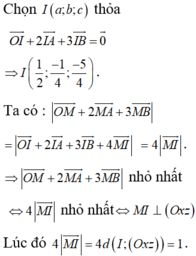Trong không gian Oxyz, hãy tìm trên mặt phẳng (Oxz) một điểm M cách đều 3 điểm \(A\left(1;1;1\right);B\left(-1;1;0\right);C\left(3;1;-1\right)\) ?
SK
Những câu hỏi liên quan
Trong không gian Oxyz, hãy tìm trên mặt phẳng (Oxz) một điểm M cách đều ba điểm A(1; 1; 1), B(-1; 1; 0), C(3; 1; -1).
Điểm M thuộc mặt phẳng (Oxz) có tọa độ là (x; 0; z), cần phải tìm x và z. Ta có:
MA 2 = 1 - x 2 + 1 + 1 - z 2
MB 2 = - 1 - x 2 + 1 + z 2
MC 2 = 3 - x 2 + 1 + - 1 - z 2
Theo giả thiết M cách đều ba điểm A, B, C nên ta có MA 2 = MB 2 = MC 2
Từ đó ta tính được 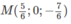
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho B(-2;2;0),C(4;1;-1),
O
A
→
2
i
→
+
2
j
→
+
2
k
→
. Trên mặt phẳng (Oxz), điểm nào dưới đây cách đều ba điểm A, B, C A. M(3/4;0;1/2) B. N(-3/4;0;(-1)/2) C. P(3/4;0;(-1)/2) D. Q(-3/4;0;1/2)
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho B(-2;2;0),C(4;1;-1), O A → = 2 i → + 2 j → + 2 k → . Trên mặt phẳng (Oxz), điểm nào dưới đây cách đều ba điểm A, B, C
A. M(3/4;0;1/2)
B. N(-3/4;0;(-1)/2)
C. P(3/4;0;(-1)/2)
D. Q(-3/4;0;1/2)
Trong không gian với hệ trục tọa độ Oxyz, cho
O
A
→
2
i
→
+
2
j
→
+
2
k
→
,
B
-
2
;
2
;
0
v
à
...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho O A → = 2 i → + 2 j → + 2 k → , B - 2 ; 2 ; 0 v à C 4 ; 1 ; - 1 . Trên mặt phẳng (Oxz), điểm nào dưới đây cách đều ba điểm A, B, C
A. N − 3 4 ; 0 ; − 1 2
B. P 3 4 ; 0 ; − 1 2
C. Q − 3 4 ; 0 ; 1 2
D. M 3 4 ; 0 ; 1 2
Trong không gian Oxyz, tập hợp các điểm M cách đều hai mặt phẳng tọa độ (Oxy) và (Oxz) là hai mặt phẳng có phương trình: A. y+z0 và y-z0 B. x+y0 và x-y0 C. x+z0 và x-z0 D. y+2z0 và y-2z0
Đọc tiếp
Trong không gian Oxyz, tập hợp các điểm M cách đều hai mặt phẳng tọa độ (Oxy) và (Oxz) là hai mặt phẳng có phương trình:
A. y+z=0 và y-z=0
B. x+y=0 và x-y=0
C. x+z=0 và x-z=0
D. y+2z=0 và y-2z=0
Đáp án A
Phương trình của hai mặt phẳng (Oxy) và (Oxz) lần lượt là z = 0 và y = 0.
Điểm M(x ;y ;z) cách đều hai mặt phẳng đó khi và chỉ khi
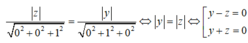
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho
O
A
→
2
i
→
+
2
j
→
+
2
k
→
, B(-2 ;2 ;0), C(4 ;1 ;-1). Trên mặt phẳng (Oxz) điểm nào dưới đây cách đều ba điểm A, B, C
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho O A → = 2 i → + 2 j → + 2 k → , B(-2 ;2 ;0), C(4 ;1 ;-1). Trên mặt phẳng (Oxz) điểm nào dưới đây cách đều ba điểm A, B, C
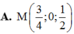

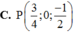
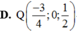
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(-1;3;4), B(3;1;0). Gọi M là điểm trên mặt phẳng (Oxz) sao cho tổng khoảng cách từ M đến A và B là ngắn nhất. Tìm hoành độ
x
0
của điểm M.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(-1;3;4), B(3;1;0). Gọi M là điểm trên mặt phẳng (Oxz) sao cho tổng khoảng cách từ M đến A và B là ngắn nhất. Tìm hoành độ x 0 của điểm M.
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai điểm
A
−
1
;
3
;
4
và
B
3
;
1
;
0
. Gọi M là điểm trên mặt phẳng
O
x
z
sao cho t ổng khoảng cách từ M đến A và B...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A − 1 ; 3 ; 4 và B 3 ; 1 ; 0 . Gọi M là điểm trên mặt phẳng O x z sao cho t ổng khoảng cách từ M đến A và B là ngắn nhất. Tìm hoành độ x 0 của điểm M.
A. x 0 = 1
B. x 0 = 2
C. x 0 = 3
D. x 0 = 4
Đáp án B.
Rõ ràng A và B đều nằm về cùng một phía đối với mặt phẳng O x z (do đều có tung độ dương). Gọi A' là điểm đối xứng của A qua O x z thì A ' = − 1 ; − 3 ; 4 . Ta có M A + M B = M A ' + M B (do M ∈ O x z và A' là điểm đối xứng của A qua O x z ). Do đó M A + M B ngắn nhất ⇔ M A ' + M B ngắn nhất ⇔ A ' , M , N thằng hàng, tức M là giao điểm của A'B và O x z .
Ta có A ' B → = 4 ; 4 ; − 4 . Suy ra phương trình đường thẳng A ' B : x = 3 + t y = 1 + t z = − t .
Phương trình mặt phẳng ( O x z ) là y=0. Giải phương trình 1 + t = 0 ⇔ t = − 1 .
Suy ra M = 2 ; 0 ; 1 . Do đó M có hoành độ bằng 2. Vậy B là đáp án đúng.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm
A
−
1
;
3
;
4
và
B
3
;
1
;
0
. Gọi M là điểm trên mặt phẳng (Oxz) sao cho t ổng khoảng cách từ M đến A và B là ngắn nhất. Tìm hoành độ
x
0
của...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A − 1 ; 3 ; 4 và B 3 ; 1 ; 0 . Gọi M là điểm trên mặt phẳng (Oxz) sao cho t ổng khoảng cách từ M đến A và B là ngắn nhất. Tìm hoành độ x 0 của điểm M.
A. x 0 = 1
B. x 0 = 2
C. x 0 = 3
D. x 0 = 4
Trong không gian Oxyz, cho các điểm A(1;1;2); B(0;-1;-3). Xét điểm M thay đổi trên mặt phẳng (Oxz), giá trị nhỏ nhất của
O
M
→
+
2
M
A
→
+
3
M
B...
Đọc tiếp
Trong không gian Oxyz, cho các điểm A(1;1;2); B(0;-1;-3). Xét điểm M thay đổi trên mặt phẳng (Oxz), giá trị nhỏ nhất của O M → + 2 M A → + 3 M B → bằng?
A. 1
B. 3 2
C. 1 2
D. 1 4