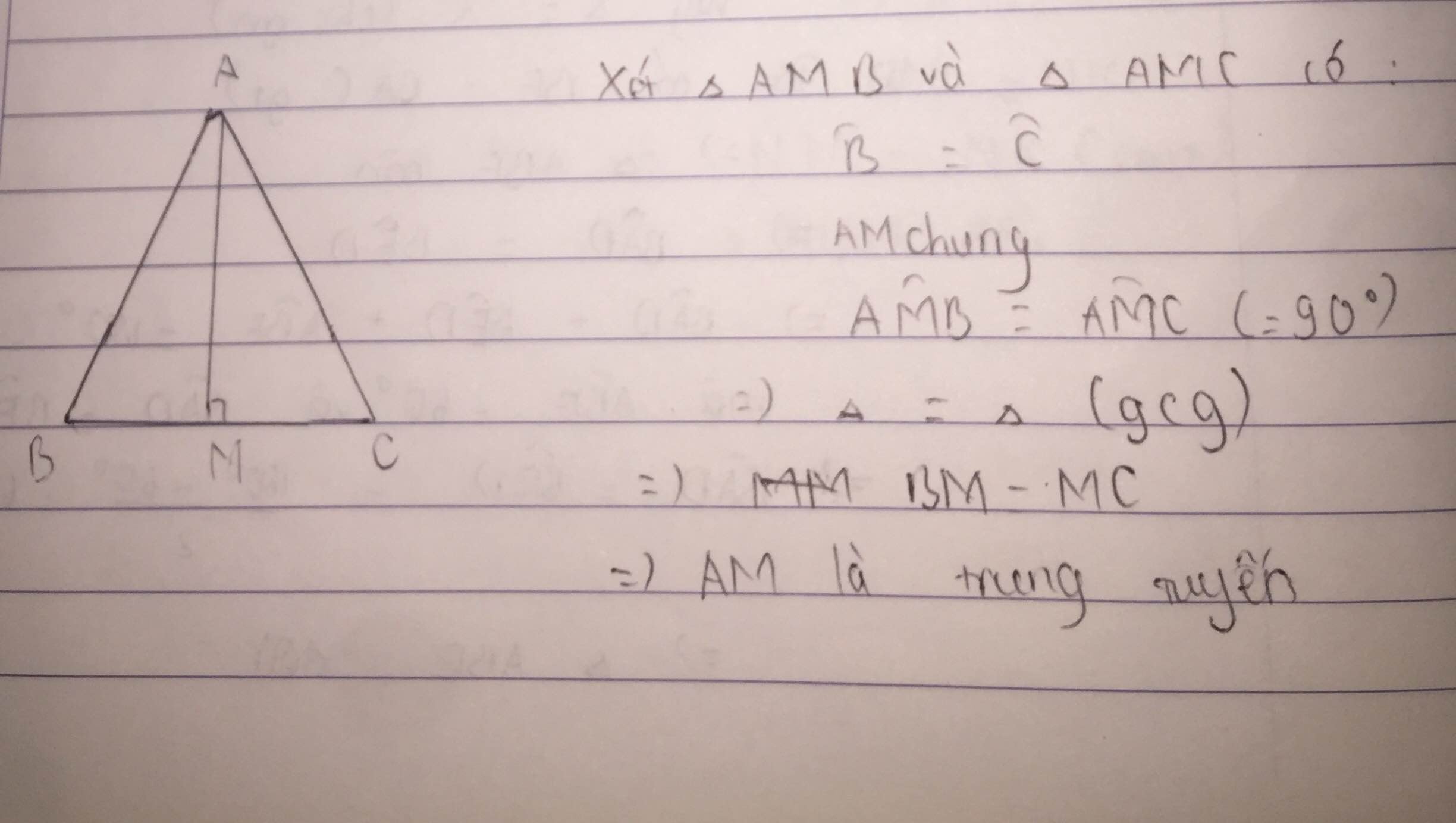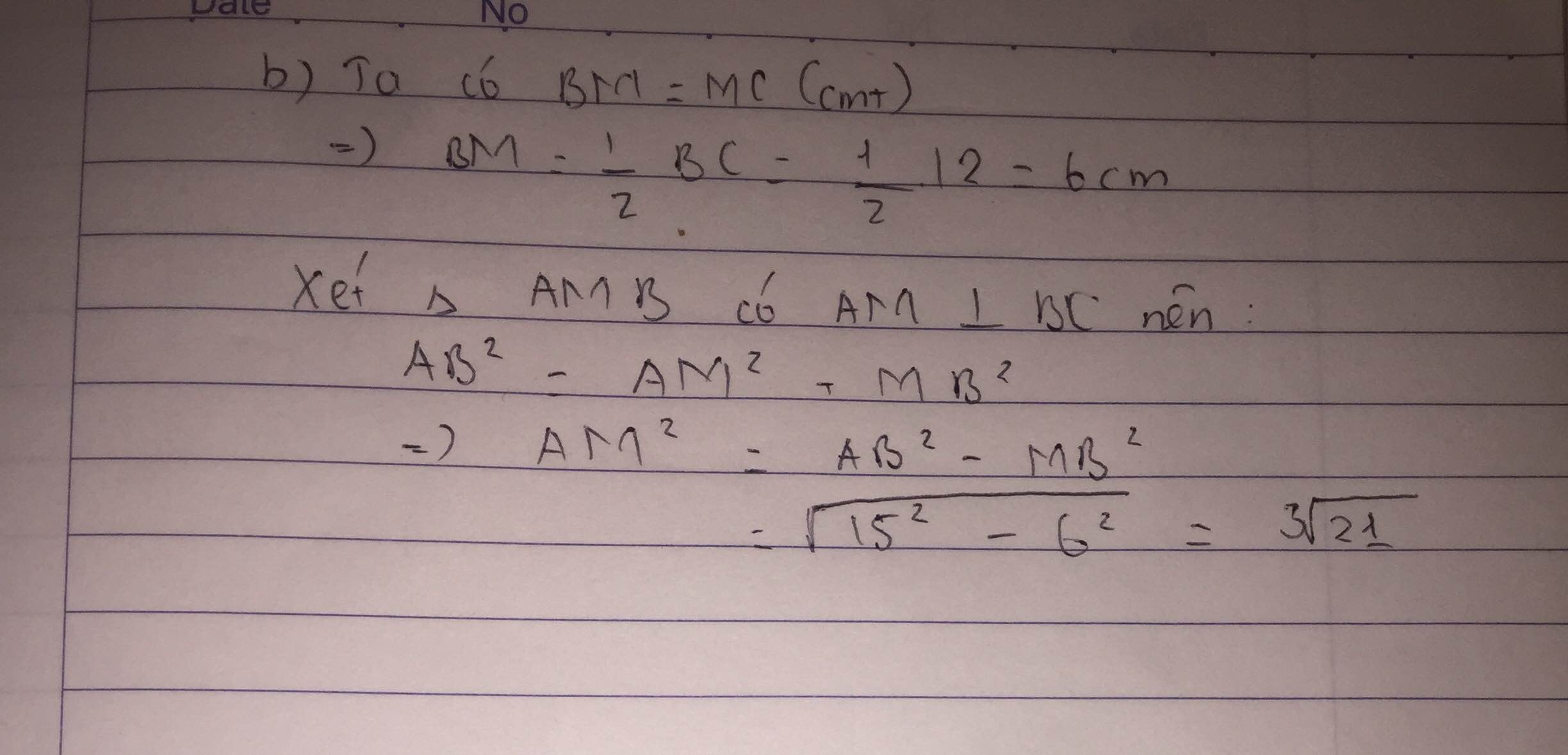cho tam giác ABC vuông tại A,trung tuyến AM.Chứng minh AM=một nủa BC
KK
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có đường cao AH,AB10cm,góc C bằng 30 độa) Tính BC,AC,AH,HBb) Kẻ phân giác AD của tam giác ABC.Tính DB,DCc) AM là trung tuyến của tam giác ABC.Gọi I là trung điểm của AD,K là trung điểm của AM.Chứng minh IKMH là hình thang.Tính diện tích của tứ giác IKMHd) Gọi E,F thứ tự là hình chiếu vuông góc của D trên AB,AC.Chứng minh AEDF là hình vuông.Tính diện tích của tứ giác BEFC
Đọc tiếp
Cho tam giác ABC vuông tại A có đường cao AH,AB=10cm,góc C bằng 30 độ
a) Tính BC,AC,AH,HB
b) Kẻ phân giác AD của tam giác ABC.Tính DB,DC
c) AM là trung tuyến của tam giác ABC.Gọi I là trung điểm của AD,K là trung điểm của AM.Chứng minh IKMH là hình thang.Tính diện tích của tứ giác IKMH
d) Gọi E,F thứ tự là hình chiếu vuông góc của D trên AB,AC.Chứng minh AEDF là hình vuông.Tính diện tích của tứ giác BEFC
a: Xét ΔABC vuông tại A có
\(BC=\dfrac{AB}{\dfrac{1}{2}}=\dfrac{10}{\dfrac{1}{2}}=20\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC=10\sqrt{3}\left(cm\right)\)
Đúng 0
Bình luận (0)
1 Cho tam giác ABC vuông ở A.trung tuyến AM.chứng minh AM=1/2 BC
2.CHo tam giác ABC.Trên tia đối tia AB lấy D sao cho AD=AB.Trên AC lấy E sao cho AE=1/3 AC .tia BE cắt CD ở M
Chứng minh: a,M là trung điểm CD
b,AM=1/2 BC
Bài 1: Cho tam giác ABC cân tại A có các đường trung tuyến BE và CD . Chứng minh rằng BE bằng CD
Bài 2: Cho tam giác ABC có đường trung tuyến BE và CD, biết BE = CD . Chứng minh rằng tam giác ABC cân tại A
Bài 3: Cho tam giác ABC chứng minh rằng a) Nếu tam giác ABC vuông góc tại A , có trung tuyến AM =1/2 BC
b) Nếu trung tuyến AM =1/2 BC thì tam giác ABC vuông góc tại A
Cho tam giác ABC có AB =9cm,AC=12cm,BC=15cm.
a) Chứng minh tam giác ABC vuông
b) Vẽ trung tuyến AM,từ M kẻ MH vuông góc AC.Trên tia đối tia MH lấy điểm K sao cho MK=MH.Chứng minh tam giác MHC=tam giác MKB
Gọi G là giao điểm của BH và AM.Chứng minh G là trọng tâm tam giác ABC
Bài làm:
a) Ta có: \(\hept{\begin{cases}AB^2+AC^2=9^2+12^2=225\left(cm\right)\\BC^2=15^2=225\left(cm\right)\end{cases}}\)
\(\Rightarrow AB^2+AC^2=BC^2\)
Áp dụng định lý Pytago đảo => Tam giác ABC vuông tại A
=> đpcm
b) Xét 2 tam giác: \(\Delta MHC\)và \(\Delta MKB\)có:
\(\hept{\begin{cases}MK=MH\left(gt\right)\\\widehat{HMC}=\widehat{KMB}\\MB=MC\left(gt\right)\end{cases}}\)(đối đỉnh)
=> \(\Delta MHC=\Delta MKB\left(c.g.c\right)\)
=> đpcm
c) Áp dụng tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông
=> \(AM=\frac{1}{2}BC=MC\)
=> Tam giác AMC cân tại M, mà MH là đường cao xuất phát từ đỉnh trong tam giác cân AMC
=> MH đồng thời là đường trung tuyến của tam giác AMC
=> H là trung điểm AC
=> BH là đường trung tuyến của tam giác ABC
Mà AG,BH là 2 đường trung tuyến của tam giác ABC cắt nhau tại G
=> G là trọng tâm tam giác ABC
=> đpcm
Học tốt!!!!
Ở đoạn xét 2 tam giác mình viết bị lỗi, bạn viết thêm cho mình MB = MC (giả thiết) nhé!
Và đoạn cuối bị lỗi
=> G là trong tâm tam giác ABC
Chúc bạn học tốt! ^ ^
cho tam giác ABC, có AB=c; AC=b;BC=a và trung tuyến AM.chứng minh rằng 4*AM^2=2*b^2+2*c^2-a^2
Cho tam giác abc vuông tại A,đường cao AH,trung tuyến AM.chứng minh:
MH/BH=2(BM/AB)^2-1
\(\Delta\)ABC vuông tại A có đường cao AH.
=> \(AB^2=BH.BC=BH.2.BM\)
=> \(\frac{1}{BH}=\frac{2BM}{AB^2}\)
=> \(\frac{BM}{BH}=2.\left(\frac{BM}{AB}\right)^2\)
=> \(\frac{BM}{BH}-1=2.\left(\frac{BM}{AB}\right)^2-1\)
=> \(\frac{HM}{BH}=2.\left(\frac{BM}{AB}\right)^2-1\)
Đúng 0
Bình luận (0)
Khai triển lại ta có
MH/BH+1=2(BM/AB)^2 <=>MB/BH=2(MB/AB)^2 <=>2BM.BH=AB^2 <=> BC.BH=AB^2
BH=BA.Cos ABC
BC=BA/cos ABC
vậy ta có điều phải cm
Đúng 1
Bình luận (0)
cho tam giác abc vuông tại a trung tuyến am chứng minh am =1/2 bc
(Bạn tự vẽ hình)
Trong tam giác vuông đường trung tuyến ứng với cạnh huyền = 1/2 cạnh huyền
=> đpcm
Đúng 0
Bình luận (0)
Bài 1. Cho tam giác ABC cân tại A. Kẻ AM vuông góc với BC tại M
a) Chứng minh AM là trung tuyến của tam giác
b) Biết AB = 15 cm; BC = 12 cm. Tính độ dài đường trung tuyến AM.
Cho tam giác ABC cân tại A, trung tuyến AM. Chứng minh rằng:
a) AM là phân giác của góc BAC?
b)AM vuông góc BC
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
=>ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông gócBC
Đúng 2
Bình luận (0)
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
=>ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông gócBC
Đúng 0
Bình luận (0)