Cho x, y, z là những số thực tùy ý.
Chứng minh rằng :
\(x^2+4y^2+3z^2+14>2x+12y+6z\)
SK
Những câu hỏi liên quan
LJ
25 tháng 10 2021 lúc 21:52
Cho số thực x, y, z thỏa mãn \(x^2+y^2+z^2-2x+4y-6z=15\). Chứng minh rằng: \(\left|2x-3y+4z-20\right|\le29\)
Giả thiết tương đương \(\left(x-1\right)^2+\left(y+2\right)^2+\left(z-3\right)^2=29\).
Áp dụng bđt Cauchy - Schwarz ta có:
\(\left(2x-3y+4z-20\right)^2=\left[2\left(x-1\right)-3\left(y+2\right)+4\left(z-3\right)\right]^2\le\left(2^2+3^2+4^2\right)\left[\left(x-1\right)^2+\left(y+2\right)^2+\left(z-3\right)^2\right]=29^2\Rightarrow\left|2x-3y+4z-20\right|\le29\)
Đúng 1
Bình luận (0)
LJ
25 tháng 10 2021 lúc 9:53
mọi người giúp em bài này ạa
Các số thực x, y, z thỏa mãn \(x^2+y^2+z^2-2x+4y-6z=15\). Chứng minh rằng \(\left|2x-3y+4z-20\right|\le29\)
chứng minh x^2 +y^2+z^2+2x-4y-6z+14 >= 0 với mọi x y z
\(x^2+y^2+z^2+2x-4y-6z+14\)
\(=\left(x^2+2x+1\right)+\left(y^2-4y+4\right)+\left(z^2-6z+9\right)\)
\(=\left(x+1\right)^2+\left(y-2\right)^2+\left(z-3\right)^2\)
Vì \(\left(x+1\right)^2\ge0\forall x\); \(\left(y-2\right)^2\ge0\forall y\); \(\left(z-3\right)^2\ge0\forall z\)
\(\Rightarrow\left(x+1\right)^2+\left(y-2\right)^2+\left(z-3\right)^2\ge0\forall x,y,z\)
hay \(x^2+y^2+z^2+2x-4y-6z+14\ge0\)\(\forall x,y,z\)
Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:
Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:
Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:
Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:
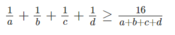
Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:
Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:
