Trong không gian Oxyz, viết phương trình mặt phẳng trung trực của đoạn thẳng AB với \(A\left(2;3;7\right);B\left(4;1;3\right)\) ?
SK
Những câu hỏi liên quan
Trong không gian Oxyz, cho hai điểm A(1;5;-2), B(3;1;2). Viết phương trình mặt phẳng trung trực của đoạn thẳng AB
A. 2x + 3y + 4 = 0
B. x - 2y + 2z - 8 = 0
C. x- 2y + 2z + 8 = 0
D. x - 2y + 2x + 2z + 4 - 0
Trong không gian với hệ tọa độ Oxyz, cho 2 điểm A(2;0;0) và B(1;1;-1). Viết phương trình mặt phẳng trung trực (P) của đoạn thẳng AB và phương trình mặt cầu tâm 0, tiếp xúc với (P)
Gọi M là trung điểm của AB, ta có \(M=\left(\frac{3}{2};\frac{1}{2};-\frac{1}{2}\right)\)
Vì (P) là mặt phẳng trung trực của AB nên (P) đi qua M và \(\overrightarrow{AB}=\left(-1;1;-1\right)\) là một vecto pháp tuyến của (P)
Suy ra, phương trình của (P) là : \(\left(-1\right)\left(x-\frac{3}{2}\right)+\left(y-\frac{1}{2}\right)+\left(-1\right)\left(z+\frac{1}{2}\right)=0\)
hay : \(2x-2y+2z-1=0\)
Ta có : \(d\left(O,\left(P\right)\right)=\frac{\left|-1\right|}{\sqrt{2^2+\left(-2\right)^2+2^2}}=\frac{1}{2\sqrt{3}}\)
Do đó phương trình mặt cầu tâm O , tiếp xúc với (P) là \(x^2+y^2+z^2=\frac{1}{12}\)
hay : \(12x^2+12y^2+12z^2-1=0\)
Đúng 0
Bình luận (0)
Trong không gian Oxyz, phương trình mặt phẳng trung trực của đoạn thẳng AB với A(1;3;2) và B(2;4;
1
2
) là
Đọc tiếp
Trong không gian Oxyz, phương trình mặt phẳng trung trực của đoạn thẳng AB với A(1;3;2) và B(2;4; 1 2 ) là
![]()
![]()
![]()
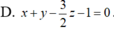
Trong không gian hệ tọa độ Oxyz, cho các điểm A(1;2;-1), B(3;0,-5) .Viết phương trình mặt phẳng trung trực của đoạn thẳng AB. A.
x
+
y
-
2
z
-
3
0
B.
x
-
y
+
2
z
-
17
0
C.
x
-
y
-
2
z
-
7
0
D.
x
+...
Đọc tiếp
Trong không gian hệ tọa độ Oxyz, cho các điểm A(1;2;-1), B(3;0,-5) .Viết phương trình mặt phẳng trung trực của đoạn thẳng AB.
A. x + y - 2 z - 3 = 0
B. x - y + 2 z - 17 = 0
C. x - y - 2 z - 7 = 0
D. x + y + 2 z - 5 = 0
Trong không gian với hệ tọa độ Oxyz, cho 2 điểm A(0;1;2), B(0;-1;2). Viết phương trình mặt phẳng trung trực của đoạn AB A. z -2 0 B. x -z +2 0 C. x 0 D. y 0
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho 2 điểm A(0;1;2), B(0;-1;2). Viết phương trình mặt phẳng trung trực của đoạn AB
A. z -2 =0
B. x -z +2 =0
C. x =0
D. y =0
Đáp án D
Trung điểm của là:
![]()
=>PT mặt phẳng trung trực của đoạn AB qua I và vuông góc với AB có PT là: y =0
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm
A
1
;
3
;
−
4
v
à
B
−
1
;
2
;
2
. Viết phương trình mặt phẳng trung trực
α
của đoạn thẳng AB. A. ...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A 1 ; 3 ; − 4 v à B − 1 ; 2 ; 2 . Viết phương trình mặt phẳng trung trực α của đoạn thẳng AB.
A. α : 4 x + 2 y + 12 z + 7 = 0
B. α : 4 x − 2 y + 12 z + 17 = 0
C. α : 4 x + 2 y − 12 z − 17 = 0
D. α : 4 x − 2 y − 12 z − 7 = 0
Trong không gian Oxyz, cho hai điểm A(1;3;-2), B(1;1;2). Gọi (P) là mặt phẳng trung trực của đoạn thẳng AB. Phương trình của mặt phẳng (P) là: A. y - 2z - 2 0 B. y - 2z - 7 0 C. y - 2z + 3 0 D. 2y + z - 4 0
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A(1;3;-2), B(1;1;2). Gọi (P) là mặt phẳng trung trực của đoạn thẳng AB. Phương trình của mặt phẳng (P) là:
A. y - 2z - 2 = 0
B. y - 2z - 7 = 0
C. y - 2z + 3 = 0
D. 2y + z - 4 = 0
Đáp án A
Mặt phẳng (P) đi qua trung điểm I của đoạn thẳng AB và vuông góc với AB.

Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho điểm A(1;-2; 3), B(3;0;-1). Mặt phẳng trung trực của đoạn thẳng AB có phương trình A.
x
-
y
-
2
z
+
1
0
B.
x
+
y
-
z
+
1
0
C.
x
+
y
-
2
z
+
7
0
D.
x
+
y
-
2...
Đọc tiếp
Trong không gian Oxyz, cho điểm A(1;-2; 3), B(3;0;-1). Mặt phẳng trung trực của đoạn thẳng AB có phương trình
A. x - y - 2 z + 1 = 0
B. x + y - z + 1 = 0
C. x + y - 2 z + 7 = 0
D. x + y - 2 z + 1 = 0
Trong không gian với hệ tọa độ Oxyz, cho A(1;2;-3), B(-3;2;9). Mặt phẳng trung trực của đoạn thẳng AB có phương trình là: A. x+3y+100 B. -4x+12z-100 C. x-3y+100 D. x-3z+100
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho A(1;2;-3), B(-3;2;9). Mặt phẳng trung trực của đoạn thẳng AB có phương trình là:
A. x+3y+10=0
B. -4x+12z-10=0
C. x-3y+10=0
D. x-3z+10=0
Đáp án D.
Gọi I là trung điểm của AB. Ta có:
![]()
Mặt phẳng trung thực của đoạn thẳng AB có phương trình là:
![]()
![]()
Đúng 0
Bình luận (0)







