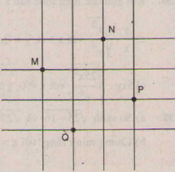
Đố: Trên lưới ô vuông, mỗi ô vuông cạnh 1 cm, cho bốn điềm M, N, P, Q (h.3)
Hãy xác định số đo cạnh, đường chéo và diện tích tứ giác MNPQ.
Đố. Trên lưới ô vuông, mỗi ô cạnh 1cm, cho bốn điểm M, N, P, Q. Hãy xác định số đô cạnh, đường chéo và diện tích của tứ giác MNPQ.
Hình 3
Dựa vào định lý Pitago, ta thấy mỗi cạnh của tứ giác MNPQ là đường chéo của hình chữ nhật do hai ô vuông ghép lại, nên hình đó có bốn cạnh bằng nhau và bằng
![]()
Tứ giác MNPQ là hình thoi có bốn cạnh bằng nhau.
Mỗi đường chéo của tứ giác MNPQ là đường chéo của hình chữ nhật do ba ô vuông ghép lại, nên giác NMPQ có hai đường chéo bằng nhau và bằng
![]()
Hình thoi MNPQ là hình vuông có hai đường chéo bằng nhau.
Diện tích hình vuông MNPQ:
S = ( √ 5 ) 2 = 5 ( c m 2 )
Đố. Trên lưới ô vuông, mỗi ô cạnh 1cm, cho bốn điểm M, N, P, Q. Hãy xác định số đô cạnh, đường chéo và diện tích của tứ giác MNPQ.
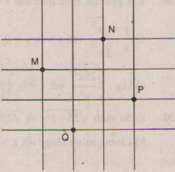
Dựa vào định lý Pitago, ta thấy mỗi cạnh của tứ giác MNPQ là đường chéo của hình chữ nhật do hai ô vuông ghép lại, nên hình đó có bốn cạnh bằng nhau và bằng
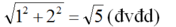
Tứ giác MNPQ là hình thoi có bốn cạnh bằng nhau.
Mỗi đường chéo của tứ giác MNPQ là đường chéo của hình chữ nhật do ba ô vuông ghép lại, nên giác NMPQ có hai đường chéo bằng nhau và bằng
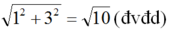
Hình thoi MNPQ là hình vuông có hai đường chéo bằng nhau.
Diện tích hình vuông MNPQ:
S = (√5)2 = 5 (cm2)
Bài 37 (trang 20 SGK Toán 9 Tập 1)
Đố. Trên lưới ô vuông, mỗi ô cạnh 1cm, cho bốn điểm M, N, P, Q. Hãy xác định số đo cạnh, đường chéo và diện tích của tứ giác MNPQ.
Nối các điểm ta có tứ giác MNPQMNPQ
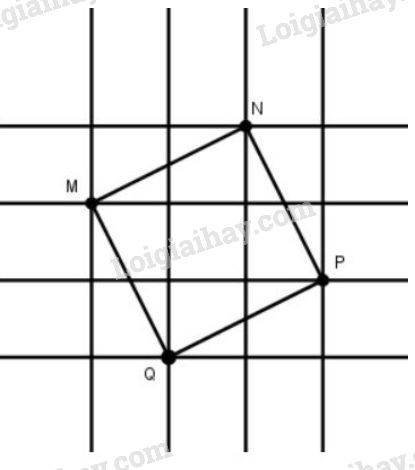
Tứ giác MNPQMNPQ có:
- Các cạnh bằng nhau và cùng bằng đường chéo của hình chữ nhật có chiều dài 2cm2cm, chiều rộng 1cm1cm. Do đó theo định lí Py-ta-go, ta có:
MN=NP=PQ=QM=√22+12=√5(cm)MN=NP=PQ=QM=22+12=5(cm).
Hay MNPQMNPQ là hình thoi.
- Các đường chéo bằng nhau và cùng bằng đường chéo của hình chữ nhật có chiều dài 3cm3cm, chiều rộng 1cm1cm nên theo định lý Py-ta-go ta có độ dài đường chéo là:
MP=NQ=√32+12=√10(cm).MP=NQ=32+12=10(cm).
Như vậy hình thoi MNPQMNPQ có hai đường chéo bằng nhau nên MNPQMNPQ là hình vuông.
Vậy diện tích hình vuông MNPQMNPQ bằng MN2=(√5)2=5(cm2)
Ta thấy mỗi cạnh của tứ giác là đường chéo của hình chữ nhật do hai ô vuông ghép lại, nên hình đó có bốn cạnh bằng nhau và bằng căn 1^2 + 2^2 = căn 5 (đvđd) (định lý Pytago)
Tứ giác có bốn cạnh bằng nhau nên tứ giác là hình thoi.
Mỗi đường chéo của tứ giác là đường chéo của hình chữ nhật do ba ô vuông ghép lại, nên giác có hai đường chéo bằng nhau và bằng căn 1^ 2 + 3^2 = căn 10 đvđ d
Hình thoi có hai đường chéo bằng nhau nên tứ giác là hình vuông.
Diện tích hình vuông :
(đvdt)
Ta thấy mỗi cạnh của tứ giác là đường chéo của hình chữ nhật do hai ô vuông ghép lại, nên hình đó có bốn cạnh bằng nhau và bằng (đvđd) (định lý Pytago)
Tứ giác có bốn cạnh bằng nhau nên tứ giác là hình thoi.
Mỗi đường chéo của tứ giác là đường chéo của hình chữ nhật do ba ô vuông ghép lại, nên giác có hai đường chéo bằng nhau và bằng (đvđd)
Hình thoi có hai đường chéo bằng nhau nên tứ giác là hình vuông.
Diện tích hình vuông :
(đvdt)
Trên lưới ô vuông, mỗi ô cạnh 1 đơn vị, người ta vẽ 8 hình vuông và tô màu khác nhau như Hình 3. Tìm dãy số biểu diễn độ dài cạnh của 8 hình vuông đỏ từ nhỏ đến lớn. Có nhận xét gì về dãy số trên?

Ta có: \({u_1} = 1;{u_2} = 1;{u_3} = 2;{u_4} = 3;{u_5} = 5;{u_6} = 8;{u_7} = 13;{u_8} = 21\)
Ta có:
\(\begin{array}{l}{u_3} = 2 = {u_2} + {u_1}\\{u_4} = 3 = {u_3} + {u_2}\\{u_5} = 5 = {u_4} + {u_3}\\{u_6} = 8 = {u_5} + {u_4}\\{u_7} = 13 = {u_6} + {u_5}\\{u_8} = 21 = {u_7} + {u_6}\end{array}\)
Ta thấy dãy số này kể từ số hạng thứ 3 bằng tổng của hai số hạng đứng trước nó.
Vậy dãy số này có công thức truy hồi là:
\(\left\{ \begin{array}{l}{u_1} = 1;{u_2} = 1\\{u_n} = {u_{n - 1}} + {u_{n - 2}}\left( {n \ge 3} \right)\end{array} \right.\)
bạn hà có một mảnh bìa hình chữ nhật dựa vào lưới ô vuông như hình vẽ hãy tính diện tích phần too đậm biết mỗi ô vuông có cạnh 1 cm
Hình vẽ ??? 🎨🎨🎨
Cho một bảng hình vuông kích thước n nhân n được chia thành lưới ô vuông đơn vị, các vị trí đỉnh của các ô vuông đơn vị được gọi là các mắt lưới. Người ta muốn đếm số lượng những hình vuông thỏa mãn hai điều kiện sau: Mỗi cạnh hình vuông phải song song với một trong hai cạnh bảng; Cả 4 đỉnh của hình vuông phải nằm tại vị trí của các mắt lưới. Ví dụ với bảng kích thước 3 nhân 3 ta có thể đếm được 14 hình vuông thỏa mãn hai điều kiện trên.
Tìm số hình vuông trên.
Cho mảnh giấy hình chữ nhật kích thước 6 cm x 8 cm người ta muốn chia mảnh giấy trên thành lưới ô vuông sao cho kích thước mỗi hình vuông là 1 số tự nhiên đơn vị cm có bao nhiêu cách trên như vậy hãy giải thích
Xét các hình A, B, C, D, E vẽ trên lưới kẻ ô vuông (h.121), mỗi ô vuông là một đơn vị diện tích.
a) Kiểm tra xem có phải diện tích hình A là diện tích 9 ô vuông, diện tích hình B cũng là diện tích 9 ô vuông hay không ?
b) Vì sao ta nói: Diện tích hình D gấp bốn lần diện tích hình C ?
c) So sánh diện tích hình C với diện tích hình E.
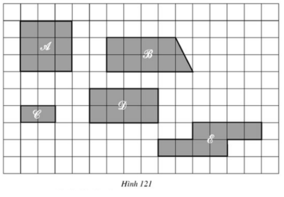
a) Diện tích hình A là 9 ô vuông (3.3 = 9)
Diện tích hình B là 9 ô vuông (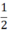 (4 + 5).2 = 9)
(4 + 5).2 = 9)
b) Diện tích hình D là 8 ô vuông (2.4 = 8)
Diện tích hình C là 2 ô vuông (2.1 = 2)
⇒ Diện tích hình D gấp 4 lần diện tích hình C
c) Diện tích hình E là 8 ô vuông
⇒ Diện tích hình E gấp 4 lần diện tích hình C
Cho một lưới gồm các ô vuông. Các nút được đánh số từ 0 đến n theo chiều từ trái sang phải và từ 0 đến m theo chiều từ dưới lên trên. Hỏi có bao nhiêu đường đi khác nhau từ nút (0,0) đến nút (n,m) nếu chỉ cho phép đi trên các cạnh ô vuông theo chiều sang phải hoặc lên trên?
Để đi từ điểm tọa độ (0,0) đến tọa độ (n,m) thì cần n bước qua phải và m bước lên trên, nên cần tổng cộng \(m+n\) bước đi để đến đích.
Chọn m bước lên trên (trong tổng số \(m+n\) bước) có \(C_{m+n}^m\) cách
Còn lại n bước, chọn n cách sang phải, có \(C_n^n\) cách
Vậy tổng cộng có: \(C_{m+n}^m.C_n^n=C_{m+n}^n\) cách
Cho một bảng hình vuông kích thước 𝑛 × 𝑛 được chia thành lưới ô vuông đơn vị, các vị trí đỉnh của các ô vuông đơn vị được gọi là các mắt lưới. Hãy đếm số những hình vuông thỏa mãn hai điều kiện sau: Mỗi cạnh hình vuông phải song song với một trong hai cạnh bảng. Cả 4 đỉnh của hình vuông phải nằm tại vị trí của các mắt lưới.