tìm tất cả các số thực z;y;z thỏa mãn
\(x\sqrt{1-y^2}+y\sqrt{2-z^2}+z\sqrt{3-x^2}=3\)
Tìm tất cả các điểm trong mặt phẳng biểu diễn số phức z thỏa mãn điều kiện 2 z là một số thực âm
A. Trục hoành (trừ gốc tọa độ O).
B. Đường thẳng y = x (trừ gốc tọa độ O).
C. Trục tung (trừ gốc tọa độ O)
D. Đường thẳng y = -x (trừ gốc tọa độ O).
Đáp án C
Giả sử ![]()
Ta có ![]()
Để
z
2
là một số thực âm thì 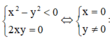
=> biểu diễn là trục tung (trừ gốc tọa độ O)
Tìm tất cả các điểm trong mặt phẳng biểu diễn số phức z thỏa mãn điều kiện 2 z là một số thực âm
A. Trục hoành (trừ gốc tọa độ O).
B. Đường thẳng y = x (trừ gốc tọa độ O).
C. Trục tung (trừ gốc tọa độ O)
D. Đường thẳng y = -x (trừ gốc tọa độ O).
Đáp án C
Giả sử z = x + y i , x , y ∈ ℝ .
Ta có z 2 = x + y i 2 = x 2 - y 2 + 2 x y i
Để z 2 là một số thực âm thì x 2 - y 2 < 0 2 x y = 0 ⇔ x = 0 y ≠ 0 ⇒ biểu diễn là trục tung (trừ gốc tọa độ O)
2. Tìm tất cả các số thực x, y, z thỏa mãn điều kiện 2sqrt(x) + 2sqrt(y - x) + 3sqrt(z - y) = 1/2 * (z + 17)
Trên tập ℂ , cho số phức z = i + m i - 1 với m là tham số thực khác -1. Tìm tất cả các giá trị của tham số m để z. z ¯ = 5
A. m = -3
B. m = 1
C. m = ± 2
D. m = ± 3
Trên tập ℂ , cho số phức z = i + m i - 1 với m là tham số thực khác -1. Tìm tất cả các giá trị của tham số m để z. z ¯ = 5
A. m = -3
B. m = 1
C. m = ± 2
D. m = ± 3
Tìm tất cả các giá trị của tham số thực m đẻ số phức z = m 2 - 1 + m + 1 i là số thuần ảo
A. m = 0
B. m = ± 1
C. m=-1
D. m=1
z = ( m 2 - 1 ) + m + 1 i là số thuần ảo ⇔ m 2 - 1 = 0 ⇔ m = ± 1
Chọn đáp án B.
Tìm tất cả các giá trị của tham số thực m đẻ số phức z = m 2 - 1 + m + 1 i là số thuần ảo
A. m = 0
B. m = ± 1
C. m = -1
D. m =1
Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất số phức z thỏa mãn z. z ¯ = 1 và |z - 3 + i|. Tìm số phần tử của S
A. 1.
B. 2.
C. 3.
D. 4
Đáp án A
Đặt z=x+yi
Ta có ![]() suy ra tập biểu diễn số phức z là đường tròn tâm M(0;0) bán kính R=1
suy ra tập biểu diễn số phức z là đường tròn tâm M(0;0) bán kính R=1
![]()
![]() (m > 0) suy ra tập biểu diễn số phức z là đường tròn tâm N(
3
;1) bán kính r=m
(m > 0) suy ra tập biểu diễn số phức z là đường tròn tâm N(
3
;1) bán kính r=m
Để tồn tại duy nhất số phức z thì 2 đường tròn phải tiếp xúc với nhau suy ra MN=R+r![]()
Vậy tập S chỉ có 1 giá trị của m
Tìm tất cả các số thực x,y,z thỏa mãn :\(x\sqrt{1-y^2}+y\sqrt{2-z^2}+z\sqrt{3-x^3}=3\)
đánh sai đề rồi bạn êi, phải là \(x\sqrt{1-y^2}+y\sqrt{2-z^2}+z\sqrt{3-x^2}=3\Leftrightarrow2x\sqrt{1-y^2}\) \(+2y\sqrt{2-z^2}+2z\sqrt{3-x^2}=6\)
<=> \(\left(x-\sqrt{1-y^2}\right)^2+\left(y-\sqrt{2-z^2}\right)^2+\left(z-\sqrt{3-x^2}\right)^2=0\)
<=> ..bla bla tự làm nhá !
Tìm tất cả các số thực x,y,z thỏa mãn :\(x\sqrt{1-y^2}+y\sqrt{2-z^2}+z\sqrt{3-x^2}=3\)
Sử dụng Bất đẳng thức Bunyakovsky cho 2 bộ 3 số \(\left(\sqrt{1-y^2};\sqrt{2-z^2};\sqrt{3-x^2}\right)\) và \(\left(x,y,z\right)\) ta có
\(\left(x\sqrt{1-y^2}+y\sqrt{2-z^2}+z\sqrt{3-x^2}\right)^2\le\left(x^2+y^2+z^2\right)\cdot\left[6-\left(x^2+y^2+z^2\right)\right]\left(1\right)\)
Đặt \(x^2+y^2+z^2=a\) ta có Bất đẳng thức (1) tương đương
\(9=\left(x\sqrt{1-y^2}+y\sqrt{2-z^2}+z\sqrt{3-x^2}\right)^2\le\left(a\right)\cdot\left(6-a\right)\)
\(=-a^2+6a-9+9=-\left(a-3\right)^2+9\le9\)
Dấu "=" xảy ra khi  Giải hệ phương trình trên ta được
Giải hệ phương trình trên ta được 
Dấu "=" xảy ra khi \(\hept{\begin{cases}a=x^2+y^2+z^2=3\\\frac{x^2}{1-y^2}=\frac{y^2}{2-z^2}=\frac{z^2}{3-x^2}=1\end{cases}}\) giải hệ pt ta có \(\hept{\begin{cases}x=1\\y=0\\z=\sqrt{2}\end{cases}}\)
Thế nào nó bị lỗi nên không hiển thị
\(z=\sqrt{2}\)nữa olm bị sao mà lỗi suất vậy