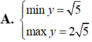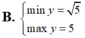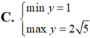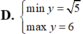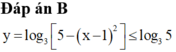Tìm Max (GTLN) của Q=-x2-2x+2021
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
OC
Những câu hỏi liên quan
Tìm GTLN (max) của hàm số
y
log
3
4
+
2
x
-
x
2
A.
log
3
4
B.
log
3
5
C.
5
3
D. ...
Đọc tiếp
Tìm GTLN (max) của hàm số y = log 3 4 + 2 x - x 2
A. log 3 4
B. log 3 5
C. 5 3
D. 1 + 3
Tìm GTLN (max), GTNN (min) của
y
x
2
-
x
+
2
x
-
1
khi
x
∈
3
2
;
3
Đọc tiếp
Tìm GTLN (max), GTNN (min) của y = x 2 - x + 2 x - 1 khi x ∈ 3 2 ; 3
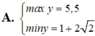
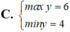
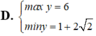
Tìm GTLN của M = 2021 – |5 – 2x| – |2x – 3|
\(M=2021-\left(|5-2x|+|2x-3|\right);G=\left(|5-2x|+|2x-3|\right)\ge|5-2x+2x-3|=2\)
do đó: \(M\le2021-2=2019\)
Ta có :
|5 – 2x| – |2x – 3| \(\ge\) |5 – 2x + 2x –3|=2M = 2021 – |5 – 2x| – |2x – 3| =>M\(\le\)2021-2=2019
=>M\(\le\)2019
Dấu "=" xảy ra khi M=2019
Vậy GTLN của M là 2019
Gấp ạ mọi người giúp em với:<
1. Q = |-2x+3| + \(\dfrac{3}{4}\)
- Tìm GTNN (Giá trị nhỏ nhất) của Q
2. H = (2x+1)\(^2\) - 1\(\dfrac{1}{2}\)
- Tìm GTNN của H
3. M = =(2x+1)\(^2\) + 2021
- Tìm GTLN (Giá trị lớn nhất) của M
3:
Ta có: \(\left(2x+1\right)^2\ge0\forall x\)
\(\Leftrightarrow\left(2x+1\right)^2+2021\ge2021\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
Tìm GTLN (max), GTNN (min) của hàm số
y
x
2
-
3
x
-
2
trên
5
2
;
5
Đọc tiếp
Tìm GTLN (max), GTNN (min) của hàm số y = x 2 - 3 x - 2 trên 5 2 ; 5
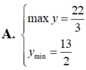
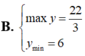
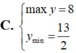

Tìm GTLN, GTNN (Max,Min) của
y
x
2
-
3
x
+
3
x
-
2
khi
x
∈
0
;
3
Đọc tiếp
Tìm GTLN, GTNN (Max,Min) của y = x 2 - 3 x + 3 x - 2 khi x ∈ 0 ; 3
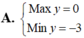
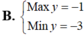

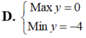
Tìm GTLN (max), GTNN (min) của
y
2
x
-
1
+
4
5
-
x
Đọc tiếp
Tìm GTLN (max), GTNN (min) của y = 2 x - 1 + 4 5 - x
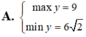
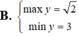
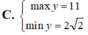
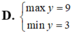
Tìm GTLN (max), GTNN (min) của
y
2
x
+
3
x
khi
x
∈
1
;
2
Đọc tiếp
Tìm GTLN (max), GTNN (min) của y = 2 x + 3 x khi x ∈ 1 ; 2
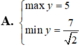
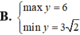
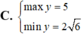
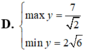
Tìm GTLN (max); GTNN (min) của hàm số
y
2
x
+
1
+
4
-
x
.
Đọc tiếp
Tìm GTLN (max); GTNN (min) của hàm số y = 2 x + 1 + 4 - x .