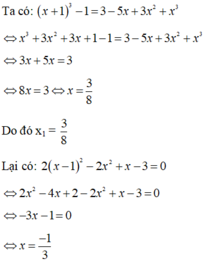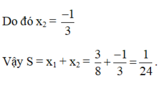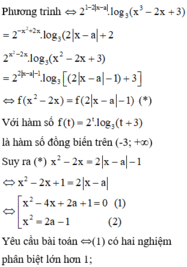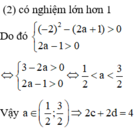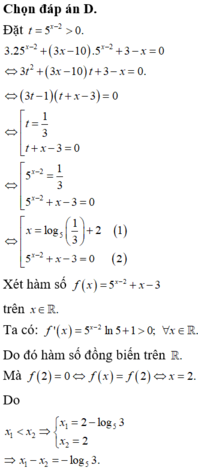Cho x1, x2, x3 là 2 nghiệm của phương trình 3x^2-5x-2=0. Khi đó A=x1+x2 có giá trị là ..
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
CB
Những câu hỏi liên quan
Cho x1, x2 là 2 nghiệm của phương trình 3x^2-5x-2=0. Khi đó A=x1+x2 có giá trị là ..
3x^2 - 5x - 2 = 0
(a = 3; b = -5; c = -2)
ta có x1, x2 là nghiệm của pt nên : x1 + x2 = -b/a = -(-5)/3 = 5/3
vậy_
Áp dụng hệ thức Vi - ét ta có : x1 + x2 = \(-\frac{b}{a}=-\frac{-5}{3}=\frac{5}{3}\)
Hoặc chưa học ở lớp 8 thì \(3x^2-5x-2=3x^2-6x+x-2=3x\left(x-2\right)+\left(x-2\right)\)
\(=\left(3x+1\right)\left(x-2\right)=0\Leftrightarrow\orbr{\begin{cases}x1=-\frac{1}{3}\\x2=2\end{cases}}\Leftrightarrow x1+x2=-\frac{1}{3}+2=\frac{5}{3}\)
\(\frac{5}{3}\) nha bn
Xem thêm câu trả lời
Gọi
x
1
là nghiệm của phương trình
x
+
1
3
– 1 3 – 5x + 3
x
2
+
x
3
và
x
2
là nghiệm của phương trình 2
x
-
1...
Đọc tiếp
Gọi x 1 là nghiệm của phương trình x + 1 3 – 1 = 3 – 5x + 3 x 2 + x 3 và x 2 là nghiệm của phương trình 2 x - 1 2 – 2 x 2 + x – 3 = 0. Giá trị S = x 1 + x 2 là:
A. 1/24
B. 7/3
C. 17/24
D. 1/3
Cho hai phương trình x2+2022x+1=0 (1) và x2+2023x+1 (2).Gọi x1,x2 là nghiệm của phương trình (1) ; x3,x4 là nghiệm của phương trình (2).Giá trị của biểu thức P=(x1+x3)(x2+x3)(x1-x4)(x2-x4) là
A.4045 B.-1 C.1 D.0
1) Cho phương trình 5x^2+3x-1=0 có hai nghiệm x1,x2. Không giải phương trình, hãy tính giá trị của biểu thức A=\(\left(3x_1+2x_2\right)\left(3x_2+x_1\right)\)
2) Cho phương trình 7x^2-2x-3=0 có hai nghiệm là x1,x2 tính giá trị của biểu thức
M=\(\dfrac{7x_1^2-2x_1}{3}+\dfrac{3}{7x_2^2-2x_2}\)
`1)` Ptr có: `\Delta=3^2-4.5.(-1)=29 > 0 =>`Ptr có `2` nghiệm phân biệt
`=>` Áp dụng Viét có: `{(x_1+x_2=[-b]/a=-3/5),(x_1.x_2=c/a=-1/5):}`
Có: `A=(3x_1+2x_2)(3x_2+x_1)`
`A=9x_1x_2+3x_1 ^2+6x_2 ^2+2x_1x_2`
`A=8x_1x_2+3(x_1+x_2)^2=8.(-1/5)+3.(-3/5)^2=-13/25`
Vậy `A=-13/25`
____________________________________________________
`2)` Ptr có: `\Delta'=(-1)^2-7.(-3)=22 > 0=>` Ptr có `2` nghiệm pb
`=>` Áp dụng Viét có: `{(x_1+x_2=[-b]/a=2/7),(x_1.x_2=c/a=-3/7):}`
Có: `M=[7x_1 ^2-2x_1]/3+3/[7x_2 ^2-2x_2]`
`M=[(7x_1 ^2-2x_1)(7x_2 ^2-2x_2)+9]/[3(7x_2 ^2-2x_2)]`
`M=[49(x_1x_2)^2-14x_1 ^2 x_2-14x_1 x_2 ^2+4x_1x_2+9]/[3(7x_2 ^2-2x_2)]`
`M=[49.(-3/7)^2-14.(-3/7)(2/7)+4.(-3/7)+9]/[3x_2(7x_2-2)]`
`M=6/[x_2(7x_2-2)]` `(1)`
Có: `x_1+x_2=2/7=>x_1=2/7-x_2`
Thay vào `x_1.x_2=-3/7 =>(2/7-x_2)x_2=-3/7`
`<=>-x_2 ^2+2/7 x_2+3/7=0<=>x_2=[1+-\sqrt{22}]/7`
`@x_2=[1+\sqrt{22}]/7=>M=6/[[1+\sqrt{22}]/7(7 .[1+\sqrt{22}]/2-2)]=2`
`@x_2=[1-\sqrt{22}]/7=>M=6/[[1-\sqrt{22}]/7(7 .[1-\sqrt{22}]/2-2)]=2`
Vậy `M=2`
Đúng 0
Bình luận (0)
Gọi x1, x2 là nghiệm của phương trình x^2+2009x+1=0,
x3,x4 là nghiệm của phương trình x^2+2010x+1=0.
Tính giá trị biểu thức (x1+x3)(x2+x3)(x1-x4)(x2-x4)
cho x1, x2, x3 là 3 nghiệm của phương trình x^3-19x-30=0. Giá trị của Bt B= x1^2 + x2^2 + x3^2 là...
x3 - 19x - 30 = 0
<=> x3 - 5x2 + 5x2 - 25x + 6x - 30 = 0
<=> x2( x - 5 ) + 5x( x - 5 ) + 6( x - 5 ) = 0
<=> ( x - 5 )( x2 + 5x + 6 ) = 0
<=> ( x - 5 )( x2 + 3x + 2x + 6 ) = 0
<=> ( x - 5 )[ x( x + 3 ) + 2( x + 3 ) ] = 0
<=> ( x - 5 )( x + 3 )( x + 2 ) = 0
đến đây dễ rồi :)
\(x^3-19x-30=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}x-5=0\\x+2=0\\x+3=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=5\\x=-2\\x=-3\end{cases}}}\)
Vậy B=x12+x22+x32
B=52+(-2)2+(-3)2
B=25+4+9
B=38
#H
Cho phương trình
4
-
x
-
a
.
log
3
x
2
-
2
x
+
3
+
2
-
x...
Đọc tiếp
Cho phương trình 4 - x - a . log 3 x 2 - 2 x + 3 + 2 - x 2 + 2 x . log 1 3 2 x - a + 2 = 0 . Tập tất cả các giá trị của tham số a để phương trình có 4 nghiệm x 1 ; x 2 ; x 3 ; x 4 thỏa mãn là (c;d). Khi đó giá trị biểu thức T = 2 c + 2 d bằng:
A. 5
B. 2
C. 3
D. 4
Cho phương trình
3
.
25
x
-
2
+
(
3
x
-
10
)
.
5
x
-
2
+
3
-
x
0
Phương trình trên có hai nghiệm x1,x2 với x1x2 Giá trị Px2-x1 bằng bao nhiêu? A.
P
log...
Đọc tiếp
Cho phương trình 3 . 25 x - 2 + ( 3 x - 10 ) . 5 x - 2 + 3 - x = 0 Phương trình trên có hai nghiệm x1,x2 với x1<x2 Giá trị P=x2-x1 bằng bao nhiêu?
A. P = log 5 3
B. P = 2 - log 5 3
C. P = 4 - log 5 3
D. P = - log 5 3
Cho phương trình
x
3
-
3
x
2
+
m
x
-
2
m
+
2
0
(m là tham số). Có bao nhiêu giá trị nguyên dương của m để phương trình có 3 nghiệm phân biệt x1,x2,x3 t...
Đọc tiếp
Cho phương trình x 3 - 3 x 2 + m x - 2 m + 2 = 0 (m là tham số). Có bao nhiêu giá trị nguyên dương của m để phương trình có 3 nghiệm phân biệt x1,x2,x3 thỏa mãn x1<1<x2<x3?
A.0
B.3
C.5
D.Vô số
Đáp án A
Ghi nhớ: Nếu hàm số ![]()
liên tục trên đoạn ![]() và
và ![]() thì phương trình
thì phương trình ![]()
có ít nhất một nghiệm nằm trong khoảng ![]() .
.
Đúng 0
Bình luận (0)