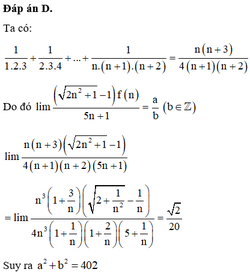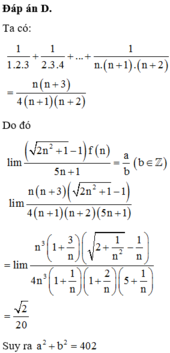1, CMR: 2n2 + 5n - 13 \(⋮\) n + 1
LD
Những câu hỏi liên quan
tìm n ∈ Z để 2n2 + 5n - 1 ⋮ 2n - 1
chứng minh rằng với mọi số nguyên n thì
a) n2(n+1) + 2n(n+1) ⋮ 6
b) (2n-1)3 - (2n-1) ⋮ 8
c) (n+7)2 - (n-5)2 ⋮ 24
1:
2n^2+5n-1 chia hết cho 2n-1
=>2n^2-n+6n-3+2 chia hết cho 2n-1
=>2n-1 thuộc {1;-1;2;-2}
mà n nguyên
nên n=1 hoặc n=0
2:
a: A=n(n+1)(n+2)
Vì n;n+1;n+2 là 3 số liên tiếp
nên A=n(n+1)(n+2) chia hết cho 3!=6
b: B=(2n-1)[(2n-1)^2-1]
=(2n-1)(2n-2)*2n
=4n(n-1)(2n-1)
Vì n;n-1 là hai số nguyên liên tiếp
nên n(n-1) chia hết cho 2
=>B chia hết cho 8
c: C=n^2+14n+49-n^2+10n-25=24n+24=24(n+1) chia hết cho 24
Đúng 0
Bình luận (1)
Cho hàm số f(n)
1
1
.
2
.
3
+
1
2
.
3
.
4
+
.
.
.
+
1
n
.
(
n
+
1
)...
Đọc tiếp
Cho hàm số f(n)= 1 1 . 2 . 3 + 1 2 . 3 . 4 + . . . + 1 n . ( n + 1 ) . ( n + 2 ) = n ( n + 3 ) 4 ( n + 1 ) ( n + 2 ) ,n∈N*. Kết quả giới hạn l i m ( 2 n 2 + 1 - 1 ) f ( n ) 5 n + 1 = a b b ∈ Z . Giá trị của a 2 + b 2 là
A. 101
B. 443
C. 363
D. 402
Cho hàm số f(n)
1
1
.
2
.
3
+
1
2
.
3
.
4
+
.
.
.
+
1
n
.
(
n
+
1
)...
Đọc tiếp
Cho hàm số f(n)= 1 1 . 2 . 3 + 1 2 . 3 . 4 + . . . + 1 n . ( n + 1 ) . ( n + 2 ) = n ( n + 3 ) 4 ( n + 1 ) ( n + 2 ) , n ∈ N * . Kết quả giới hạn lim ( 2 n 2 + 1 - 1 ) f ( n ) 5 n + 1 = a b ( b ∈ Z ) . Giá trị của a 2 + b 2 là
A.101
B.443
C.363
D.402
Viết biểu thức sau với dạng bình phương một tổng:
(2n2 + 5n)(2n2 + 5n + 12) + 36
Giúp với ạ
\(=\left(2n^2+5n\right)\left(2n^2+5n\right)+12\left(2n^2+5n\right)+36=\left(2n^2+5n\right)^2+2.\left(2n^2+5n\right).6+6^2=\left(2n^2+5n+6\right)^2\)
Đúng 2
Bình luận (0)
Kết quả l i m ( 7 n 4 + 2 n 2 - 5 n ) bằng:
A. -∞
B. 4
C. 7
D. +∞
CMR với mọi n thuộc N ta có:
1/1.6+1/6.11+....+1/(5n+1)(5n+6) = n+1/5n+6
Ta có:
\(\frac{1}{1.6}+\frac{1}{6.11}+...+\frac{1}{\left(5n+1\right)\left(5n+6\right)}=\frac{1}{5}\left(\frac{1}{1}-\frac{1}{6}+\frac{1}{6}-\frac{1}{11}+...+\frac{1}{5n+1}-\frac{1}{5n+6}\right)\)
\(=\frac{1}{5}\left(\frac{1}{1}-\frac{1}{5n+6}\right)=\frac{1}{5}\left(\frac{5n+6}{5n+6}-\frac{1}{5n+6}\right)=\frac{1}{5}.\frac{5n+5}{5n+6}=\frac{1}{5}.\frac{5\left(n+1\right)}{5n+6}=\frac{5\left(n+1\right)}{5\left(5n+6\right)}=\frac{n+1}{5n+6}\)(ĐPCM)
Đúng 0
Bình luận (0)
bạn Phạm Thiết Tường ơi ch mình hỏi sao lại nhân \(\frac{1}{5}\)với \(\frac{1}{1}-\frac{1}{5n+6}\)vậy
Đúng 0
Bình luận (0)
@tranlethanhtruc: Bn ấy lm sai.
CMR:1/1x6+1/6x11+1/11x16+....+1/(5n+1)(5n+6)=n+1/5n+6
Gọi A = 1/1.6 + 1/6.11 +...+ 1/(5n+1)(5n+6)
5A = 5/1.6 + 5/6.11 + ... + 5/(5n+1)(5n+6)
=1 - 1/6 + 1/6 - 1/11 + ... + 1/5n+1 - 1/5n+6
=1 - 1/5n+6 =5n+6/5n+6 - 1/5n+6=5n+5 /5n+6
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
CMR : với mọi n thuộc N thì ta luôn có :
1/6+1/66+1/176+...+1/(5n+1)(5n+6)=n+1/5n+6
CMR :phân số tối giản
a,\(\dfrac{4n-13}{5n-16}\)
b,\(\dfrac{5n-13}{3n-8}\)
â) Gọi \(d=ƯCLN\left(4n-13;5n-16\right)\left(d\in N\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}4n-13⋮d\\5n-16⋮d\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}20n-65⋮d\\20n-64⋮d\end{matrix}\right.\)
\(\Leftrightarrow1⋮d\)
Vì \(d\in N;1⋮d\Leftrightarrow d=1\)
\(\LeftrightarrowƯCLN\left(4n-13;5n-16\right)=1\)
\(\Leftrightarrow\) Phân số \(\dfrac{4n-13}{5n-16}\) tối giản với mọi n
b) Gọi \(d=ƯCLN\left(5n-13;3n-8\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}5n-13⋮d\\3n-8⋮d\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}15n-39⋮d\\15n-40⋮d\end{matrix}\right.\)
\(\Leftrightarrow1⋮d\)
Vì \(d\in N;1⋮d\Leftrightarrow d=1\)
\(\LeftrightarrowƯCLN\left(5n-13;3n-8\right)=1\)
\(\Leftrightarrow\) Phân số \(\dfrac{5n-13}{3n-8}\) tối giản với mọi n
Đúng 0
Bình luận (0)
a) \(\dfrac{4n-13}{5n-16}\)
Đặt \(d=ƯCLN\left(4n-13;5n-16\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}4n-13⋮d\\5n-16⋮d\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5\left(4n-13\right)⋮d\\4\left(5n-16\right)⋮d\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}20n-65⋮d\\20n-64⋮d\end{matrix}\right.\)
\(\Leftrightarrow\left(20n-65\right)-\left(20n-64\right)⋮d\)
\(\Leftrightarrow20n-65-20n+64⋮d\)
\(\Leftrightarrow-1⋮d\)
\(\Leftrightarrow d=\left\{1;-1\right\}\)
Vậy phân số \(\dfrac{4n-13}{5n-16}\) là phân số tối giản.
Đúng 0
Bình luận (0)
b) \(\dfrac{5n-13}{3n-8}\)
Đặt \(d=ƯCLN\left(5n-13;3n-8\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}5n-13⋮d\\3n-8⋮d\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3\left(5n-13\right)⋮d\\5\left(3n-8\right)⋮d\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}15n-39⋮d\\15n-40⋮d\end{matrix}\right.\)
\(\Leftrightarrow\left(15n-39\right)-\left(15n-40\right)⋮d\)
\(\Leftrightarrow15n-39-15n+40⋮d\)
\(\Leftrightarrow1⋮d\)
\(\Leftrightarrow d=1\)
Vậy phân số \(\dfrac{5n-13}{3n-8}\) là phân số tối giản.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời