Với a<2b<0, rút gọn \(\dfrac{1}{a-2b}\)√b2(a2-4ab+4b2)
NT
Những câu hỏi liên quan
(a^2 +b^2 -1)-(a.b^2-a) với a -1 , b 25(a^2 +b(a^2 +b^2 -1)-(a.b^2-a) với a -1 , b 25(a^2 +b^2 -1)-(a.b^2-a) với a -1 , b 25(a^2 +b^2 -1)-(a.b^2-a) với a -1 , b 25(a^2 +b^2 -1)-(a.b^2-a) với a -1 , b 25(a^2 +b^2 -1)-(a.b^2-a) với a -1 , b 25(a^2 +b^2 -1)-(a.b^2-a) với a -1 , b 25(a^2 +b^2 -1)-(a.b^2-a) với a -1 , b 25(a^2 +b^2 -1)-(a.b^2-a) với a -1 , b 25(a^2 +b^2 -1)-(a.b^2-a) với a -1 , b 25(a^2 +b^2 -1)-(a.b^2-a) với a -1 , b 25(a^2 +b^2 -1)-(a.b^2-a) với a -1 , b 25(a^2 +b^2 -1)-(a.b^2-a) v...
Đọc tiếp
(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25^2 -1)(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25-(a.b^2-a) với a= -1 , b=(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25 25(a^2 +b^2 -1)-(a.b^2(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25-a) với a= -1 (a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25=5 25
một câu hỏi rất đáng khen ,.. very good!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Rút gọn các biểu thức sau :
a) √(2-√3)^2
b) √(3-√11)^2
c) 2√a^2 với a>=0
d) 3√(a-2)^2 với a>2
e) √a^6 với a<0
f) 2√a^2 -5a với a<0
g) √25a^2 + 3a với a>=0
h) √9a^4 + 3a^2
i) 5√4a^6 - 3a^3 với a<0
j) 3√(3-a)^2 - 2a với a>3
a)\(\sqrt{\left(2-\sqrt{3}\right)^2}=2-\sqrt{3}\)
b)\(\sqrt{\left(2-\sqrt{11}\right)^2}=2-\sqrt{11}\)
c)\(2\sqrt{a^2}=2a\) vì a≥0
Đúng 0
Bình luận (3)
Cho ba đường thẳng a ; b ; c . chọn đáp án đúng
A. Nếu a vuông góc với b và c vuông góc với b thì a vuông góc với c
B. Nếu a vuông góc với b và c song song với b thì a song song với c
C. Nếu a song song với b và b song song với c thì a vuông góc với c
D. Nếu a vuông góc với b và c song song vói b thì a vuông góc với c
Hệ thức nào sau đây phù hợp với quá trình nén khí đẳng nhiệt ?
A. Q + A = 0 với A < 0
B. ∆ U = Q + A với ∆ U > 0 ; Q < 0 ; A > 0.
C. Q + A = 0 với A > 0.
D. ∆ U = A + Q với A > 0 ; Q < 0.
Trường hợp nào sau đây ứng với quá trình đẳng tích khi nhiệt độ tăng?
A. ΔU = Q với A > 0
B. ΔU = Q + A với A > 0
C. ΔU = Q + A với A < 0
D. ΔU = Q với Q < 0
- Chọn A.
- Vì trong quá trình đẳng tính nhiệt lượng mà khí nhận được chỉ để làm tăng nội năng của khí.
Đúng 0
Bình luận (0)
Nguyên tắc bổ sung trong quá trình dịch mã biểu hiện là sự liên kết giữa các nuclêôtit
A. A liên kết với U; G liên kết với X
B. A liên kết với T; G liên kết với X
C. A liên kết với X; G liên kết với T
D. A liên kết với U; T liên kết với X
Xem thêm câu trả lời
Cho 3 Đường thẳng phân biệt a,b,c:
a.nếu a vuông góc với b và b vuông góc với c thì a vuông góc với c
b.nếu a vuông góc với b và b vuông góc với c thì a // với c
c.nếu a // b và b // c thì a // với c
d.nếu a // b và b // c thì a vuông goc với c
Hãy chọn đáp án đung
Rút gọn các biểu thức sau:
a
)
a
b
2
3
a
2
b
4
v
ớ
i
a
0
;
b
≠
0
b
)
27...
Đọc tiếp
Rút gọn các biểu thức sau:
a ) a b 2 3 a 2 b 4 v ớ i a < 0 ; b ≠ 0 b ) 27 a - 3 2 48 v ớ i a > 3 c ) 9 + 12 a + 4 a 2 b 2 v ớ i a ≥ - 1 , 5 v à b < 0 d ) a - b a b a - b 2 v ớ i a < b < 0
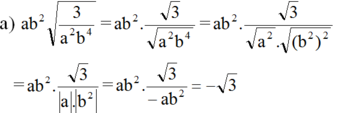
(vì a < 0 nên |a| = -a, b2 > 0 với mọi b ≠ 0 nên |b2| = b2 )
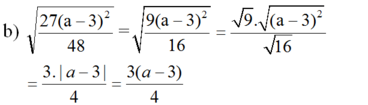
(vì a > 3 nên |a - 3| = a - 3)
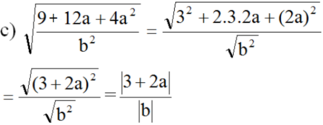
Vì b < 0 nên |b| = -b
Vì a ≥ -1,5 nên 3 + 2a ≥ 0. Do đó: |3 + 2a| = 3 + 2a
Vậy:
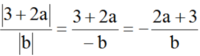
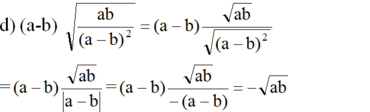
(vì a < b < 0 và b < 0 nên |a - b| = -(a - b), ab > 0)
Đúng 0
Bình luận (0)
Hệ thức nào sau đây phù hợp với quá trình làm lạnh khí đẳng tích ?
A. ∆ U = Q với Q > 0. B. ∆ U = A với A > 0.
C. ∆ U = A với A < 0. D. ∆ U = Q với Q < 0.
A)giảm dần : a , a-1 , a-2 với a thuộc N , a ≥ 2
A+1 , b , b-1 với b thuộc N , b > 1
B)tăng dần : a, a+1 , a+2 với a thuộc N
b-2 , b -1 , b với với b thuộc N , b ≥ 2







