Cho tam giác ABC cân tại A có góc BAC = 100 độ. Tia phân giác của góc B cắt AC tại D.CMR: BC=BD+AD
KK
Những câu hỏi liên quan
Cho tam giác ABC cân tại A có góc BAC = 100 độ. Tia phân giác của góc B cắt AC tại D.CMR: BC=BD+AD
Cho tam giác ABC cân tại A có góc A = 100 độ tia phân giác của góc ABC cắt AC tại D . Chứng Minh AD + BD = BC
trên tia BC lấy M,N sao cho góc BDN=6O* , BDM=80*
CM được tam giáC BDN=BDA( g-c-g)
=> AD=DN , góc DNB=DAB=100*
=> DNC=80* = DMB
=> DN=DM =DA=MC(Tự chứng minh)
=>đpcm
Đúng 0
Bình luận (0)
Tam giác ABC cân tại A . Góc BAC =100*. Tia phân giác của góc ABC cắt AC tại D . Trên BC lấy K . Góc BDK = 60*.
A, tính góc ABC,ACB
B, cm DA = DK
C, cm BC = BD+AD
Xem chi tiết
a) Ta có: ΔABC cân tại A(gt)
nên \(\widehat{ABC}=\dfrac{180^0-\widehat{BAC}}{2}\)(Số đo của một góc ở đáy trong ΔABC cân tại A)
\(\Leftrightarrow\widehat{ABC}=\dfrac{180^0-100^0}{2}=40^0\)
Ta có: ΔABC cân tại A(gt)
nên \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy)
hay \(\widehat{ACB}=40^0\)
Vậy: \(\widehat{ABC}=40^0\); \(\widehat{ACB}=40^0\)
Đúng 1
Bình luận (0)
cho tam giác ABC cân tại A. Có góc A bàng 100 độ. Tia phân giác góc B cắt AC tại D. CHứng minh BC = AD + BD
cho tam giác ABC cân tại A có góc A = 100 độ. Tia phân giác của góc B cắt AC ở D. Chứng minh rằng BC = BD + AD.
Câu hỏi của Phạm Thùy Dung - Toán lớp 7 - Học toán với OnlineMath
cho tam giac ABC cân tại A có A=110 độ, tia phân giác của ABC cắt AC tại D.CMR AD+BD=BC
Cho tam giác ABC cân tại A góc A=100 độ, tia phân giác góc B cắt AC tại D. Chứng minh: BC=BD+AD
Tren Tia bc lay diem g sao cho bd=bg suy ra tg dbg can tai b suy ra bgd=bdg
Cmd abc=acb=40 do
bd la Tia phan giac cua abc suy ra abd=cbd=20
ta co tg dbg can tai b
ma dbg=20
tu 2 dieu tren cmd bdg=bgd=80
cmd adb=60 suy ra bdc=120
cmd dcg=40
cmd dgc =100
ta co dgc=100 ma dcg =40 cmd tg dgc can tai g suy ra dg =gc
Đúng 0
Bình luận (0)
Bạn Luong Ngoc Quynh Nhu ơi bạn làm như vậy ko được bởi vì bạn lấy 2 điểm G, N khác nhau nên ko làm được. Cách này chỉ CM được 1 cái thôi
Đúng 1
Bình luận (0)
bài cần chứng minh BC=BD+AD mà bạn làm sai rồi
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC cân tại A ( góc A = 100 độ). Tia phân giác của góc ABC cắt AC tại D. Chứng minh rằng BD + AD = BC
Trên cạnh BC lấy điểm E sao cho BD=BE.
Dễ thấy: ^DBE = ^ABC/2 = 400/2 = 200 => ^BED = ^BDE = (1800 - ^DBE)/2 = 800 => ^DEC = 1000
Tam giác DEC có: ^DEC = 1000; ^ECD = ^ACB = 400 => Tam giác DEC cân tại E => ED=EC
Dễ dàng c/m được AD=ED (Gợi ý: Hạ DH, DK vuông góc AB,BC). Từ đó: EC = AD
Vậy thì BC = BE + EC = BD + AD (đpcm).
Đúng 2
Bình luận (0)
Cho tam giác cân ABC có góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Chứng minh rằng BC = BD + AD
\(\Delta\)BAC có:
BAC^ = 100o
ABC^ = ACB^
và BAC^ + ABC^ + ACB^ = 180o
2* ABC^ = 180o - BAC^
= 180o - 100o
= 80o
=> ABC^ = 40o
Ta có: DBE^ = ABC^/2 = 40o/2 = 20o
Kẻ BE = BD (E thuộc BC)
=> \(\Delta\)DBE cân tại B
=> BDE^ = BED^
\(\Delta\)DBE có:
DBE^ + BDE^ + BED^ = 180o
20o + 2* BDE^ = 180o
2* BDE^ = 160o
BDE^ = 80o
Ta có: BDA^ + BDE^ + EDC^ = 180o
EDC^ = 180o - BDA^ - BDE^
= 180o - 60o - 80o
= 40o (1)
Mà ACB^ = ABC^ = 40o (2)
Từ (1) và (2) => EDC^ = ACB^ hay EDC^ = ECD^
=> \(\Delta\)DEC cân tại E
=> DE= CE
Ta có: BC = BE + EC
mà BE = BD và DE = EC
=> BC = BD + DE
Chết rồi! Làm sao để chứng minh DE = DA !!!!!!!!!!??????
Ko làm nữa đâu, 1 bài toán mà mất 1h luôn T_T!!!!!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác cân ABC có góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Chứng minh rằng BC = BD + AD





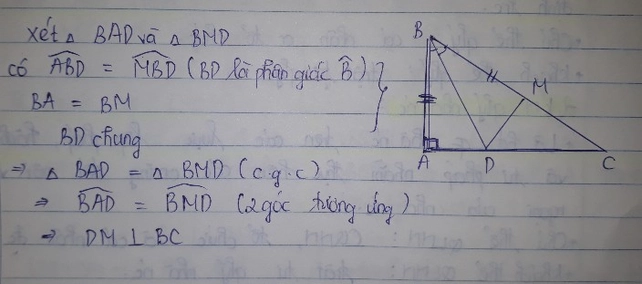 Đây là bài làm tương tự bạn tham khảo nhé!
Đây là bài làm tương tự bạn tham khảo nhé!

