Chứng minh rằng: 20 + 21 + 22 + 23 +... + 2n = 2n+1 - 1 (n \(\in\) N*)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
NM
Những câu hỏi liên quan
Chứng minh rằng :
a) \(\dfrac{1.3.5.....39}{21.22.23.....40}=\dfrac{1}{2^{20}}\)
b) \(\dfrac{1.3.5....\left(2n-1\right)}{\left(n+1\right)\left(n+2\right)\left(n+3\right)...2n}=\dfrac{1}{2^n}\) với \(n\in\) N*
a) Vế trái \(=\dfrac{1.3.5...39}{21.22.23...40}=\dfrac{1.3.5.7...21.23...39}{21.22.23....40}=\dfrac{1.3.5.7...19}{22.24.26...40}\)
\(=\dfrac{1.3.5.7....19}{2.11.2.12.2.13.2.14.2.15.2.16.2.17.2.18.2.19.2.20}\\ =\dfrac{1.3.5.7.9.....19}{\left(1.3.5.7.9...19\right).2^{20}}=\dfrac{1}{2^{20}}\left(đpcm\right)\)
b) Vế trái
\(=\dfrac{1.3.5...\left(2n-1\right)}{\left(n+1\right).\left(n+2\right).\left(n+3\right)...2n}\\ =\dfrac{1.2.3.4.5.6...\left(2n-1\right).2n}{2.4.6...2n.\left(n+1\right)\left(n+2\right)...2n}\\ =\dfrac{1.2.3.4...\left(2n-1\right).2n}{2^n.1.2.3.4...n.\left(n+1\right)\left(n+2\right)...2n}\\ =\dfrac{1}{2^n}.\\ \left(đpcm\right)\)
Đúng 5
Bình luận (0)
(f) Chứng minh rằng với mọi số tự nhiên n 1 thì: 5^n+2 + 26.5^n + 82n+1 chia hết cho 59.(g) Chứng minh rằng với mọi số tự nhiên n 1 thì số 4^2n+1 + 3^n+2chia hết cho 13.(h) Chứng minh rằng với mọi số tự nhiên n 1 thì số 5^2n+1 + 2^n+4+ 2^n+1 chia hết cho 23.(i) Chứng minh rằng với mọi số tự nhiên n 1 thì số 11n+2 + 122n+1 chia hết cho 133.(j) Chứng minh rằng với mọi số tự nhiên n 1: 5^2n−1 .26n+1 + 3^n+1 .2^2n−1 chia hết cho 38
Đọc tiếp
(f) Chứng minh rằng với mọi số tự nhiên n > 1 thì: 5^n+2 + 26.5^n + 82n+1 chia hết cho 59.
(g) Chứng minh rằng với mọi số tự nhiên n > 1 thì số 4^2n+1 + 3^n+2chia hết cho 13.
(h) Chứng minh rằng với mọi số tự nhiên n > 1 thì số 5^2n+1 + 2^n+4+ 2^n+1 chia hết cho 23.
(i) Chứng minh rằng với mọi số tự nhiên n > 1 thì số 11n+2 + 122n+1 chia hết cho 133.
(j) Chứng minh rằng với mọi số tự nhiên n > 1: 5^2n−1 .26n+1 + 3^n+1 .2^2n−1 chia hết cho 38
1+2+3+4+5+6+7+8+9=133456 hi hi
đào xuân anh sao mày gi sai hả
???????????????????
Xem thêm câu trả lời
Đề bài: Chứng minh rằng 1.3.5. … .(2n-1) / (n+1).(n+2). … .2n = 1/2n. Đề bài: Chứng minh rằng 1.3.5. … .(2n-1) / (n+1).(n+2). … .2n = 1/2n.
Ta có: 1.3.5...(2n - 1) = { [1.3.5....(2n - 1)].(2.4.6...2n) }/(2.4.6...2n) = (1.2.3.4....2n)/[ (1.2).(2.2).(3.2)...(n.2) ] = {(1.2.3.4...n).[ (n + 1)(n + 2)...2n ] }/[ (1.2.3..n)(2.2.2...2) ] = [ (n + 1)(n + 2)...2n ]/(2.2.2...2) => 1.3.5...(2n - 1) = [ (n + 1)(n + 2)...2n ]/(2.2.2...2) Do n ∈ Z+ => 1.3.5...(2n - 1) thuộc nguyên dương => [ (n + 1)(n + 2)...2n ]/(2.2.2...2) thuộc nguyên dương => [ (n + 1)(n + 2)...2n ] chia hết cho (2.2.2...2) Bây giờ ta cần tìm số chữ số 2 trong cụm (2.2.2....2) Ta thấy: 2 -> 2n có (2n - 2)/2 + 1 = n chữ số => trong cụm (2.2.2...2) có n chữ số 2 (Vì trong mỗi số từ 2 -> 2n ta đều lấy ra 1 số 2) => [ (n + 1)(n + 2)...2n ] chia hết cho 2^n
Đúng 0
Bình luận (0)
Ta có: 1.3.5...(2n - 1)
= { [1.3.5....(2n - 1)].(2.4.6...2n) }/(2.4.6...2n)
= (1.2.3.4....2n)/[ (1.2).(2.2).(3.2)...(n.2) ]
= {(1.2.3.4...n).[ (n + 1)(n + 2)...2n ] }/[ (1.2.3..n)(2.2.2...2) ]
= [ (n + 1)(n + 2)...2n ]/(2.2.2...2)
=> 1.3.5...(2n - 1) = [ (n + 1)(n + 2)...2n ]/(2.2.2...2)
Do n ∈ Z+ => 1.3.5...(2n - 1) thuộc nguyên dương
=> [ (n + 1)(n + 2)...2n ]/(2.2.2...2) thuộc nguyên dương
=> [ (n + 1)(n + 2)...2n ] chia hết cho (2.2.2...2)
Bây giờ ta cần tìm số chữ số 2 trong cụm (2.2.2....2)
Ta thấy: 2 -> 2n có (2n - 2)/2 + 1 = n chữ số => trong cụm (2.2.2...2) có n chữ số 2 (Vì trong mỗi số từ 2 -> 2n ta đều lấy ra 1 số 2)
=> [ (n + 1)(n + 2)...2n ] chia hết cho 2^n
Đúng 0
Bình luận (0)
Chứng minh rằng : 1/20 .21 + 1/22 . 23 + ....... + 1/79.80 < 1
1/20 .21 + 1/22 .23 + .... + 1/79 .80
= 1/20 - 1/21 + 1/22 - 1/23 + .......... + 1/79 - 1/80
= 1/20 - 1/80
= 3/80
Ta thấy : 3/80 < 1
=> 1/20 . 21 + 1/22 . 23 + ........ + 1/79 . 80 <1 (ĐPCM)
Đúng 1
Bình luận (0)
Chứng minh rằng \(2^{n+1}.5^{2n-1}+2^{2n-1}.3^{n+1}⋮38\left(n\in N,n\ge1\right)\)
Chứng minh rằng:(2n+3)2-(2n-1)2 chia hết cho 8 với n \(\in\) Z
EZ NUB BRO CRY :>
Giả sử : A=(2n+3)2-(2n-1)2
=(4n2+12n+9)-(4n2-4n+1)
=(4n2-4n2)+(12n+4n)+(9-1)
=16n+8
=8(2n+1) ⋮ 8
Vậy A⋮8 (đpcm)
học lại hàng đẳng thức đáng nhớ đi bro :>
Đúng 0
Bình luận (0)
Cho \(M=\dfrac{1.3.5.7.....\left(2n-1\right)}{\left(n+1\right)\left(n+2\right)\left(n+3\right).....2n}\) với \(n\in\) N* .
Chứng minh rằng \(M< \dfrac{1}{2^{n-1}}\)
Lời giải:
\(M=\frac{1.2.3.4.5.6.7...(2n-1)}{2.4.6...(2n-2).(n+1)(n+2)....2n}=\frac{(2n-1)!}{2.1.2.2.2.3...2(n-1).(n+1).(n+2)...2n}\)
\(=\frac{(2n-1)!}{2^{n-1}.1.2...(n-1).(n+1).(n+2)....2n}=\frac{(2n-1)!}{2^{n-1}.1.2...(n-1).n(n+1)..(2n-1).2}\)
\(=\frac{(2n-1)!}{2^{n-1}.(2n-1)!.2}=\frac{1}{2^{n-1}.2}<\frac{1}{2^{n-1}}\)
Ta có đpcm.
Đúng 1
Bình luận (0)
Cho n là nghiệm của
C
1
n
+
C
n
n
-
1
4040
, khi đó tổng
S
2
1
-
1
1
C
n
0
+...
Đọc tiếp
Cho n là nghiệm của C 1 n + C n n - 1 = 4040 , khi đó tổng S = 2 1 - 1 1 C n 0 + 2 2 - 1 2 C n 1 + 2 3 - 1 3 C n 2 + . . . + 2 n + 1 - 1 n + 1 C n n bằng
A. 3 2022 + 2 2021
B. 3 2021 - 2 2021 2021
C. 3 2020 - 2 2021 2021
D. 3 2021 - 2 2021 2020
Cho n là nghiệm của
C
n
1
+
C
n
n
-
1
4040
. Khi đó tổng
S
2
1
-
1
1
C
n
0
+
2...
Đọc tiếp
Cho n là nghiệm của C n 1 + C n n - 1 = 4040 . Khi đó tổng S = 2 1 - 1 1 C n 0 + 2 2 - 1 2 C n 1 + 2 3 - 1 3 C n 2 + . . . + 2 n + 1 - 1 n + 1 C n n bằng

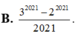
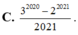
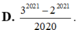
chứng minh rằng: \(n^4+2n^3-n^2-2n\) chia hết cho 21 với N\(\in\)Z